+ - 0:00:00
Notes for current slide
Notes for next slide

4.2: Difference-in-Difference Models

ECON 480 · Econometrics · Fall 2019

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsf19
metricsF19.classes.ryansafner.com

Clever Research Designs Identify Causality

Again, this toolkit of research designs to identify causal effects is the economist's comparative advantage that firms and governments want!

Difference-in-Difference Models

Difference-in-Difference Models I

  • Often, we want to examine the consequences of a change, such as a law or policy

Difference-in-Difference Models I

  • Often, we want to examine the consequences of a change, such as a law or policy

  • Example: how do States that implement law X see changes in Y

    • Treatment: States that implement law X
    • Control: States that did not implement law X

Difference-in-Difference Models I

  • Often, we want to examine the consequences of a change, such as a law or policy

  • Example: how do States that implement law X see changes in Y

    • Treatment: States that implement law X
    • Control: States that did not implement law X

  • If we have panel data with observations for all states before and after the change...

  • Find the difference between treatment & control groups in their differences before and after the treatment period

Difference-in-Difference Models I

  • Often, we want to examine the consequences of a change, such as a law or policy

  • Example: how do States that implement law X see changes in Y

    • Treatment: States that implement law X
    • Control: States that did not implement law X

  • If we have panel data with observations for all states before and after the change...

  • Find the difference between treatment & control groups in their differences before and after the treatment period

Difference-in-Difference Models II

  • The difference-in-difference model (aka "diff-in-diff" or DND") identifies treatment effect by differencing the difference pre- and post-treatment values of Y between treatment and control groups

Difference-in-Difference Models II

  • The difference-in-difference model (aka "diff-in-diff" or DND") identifies treatment effect by differencing the difference pre- and post-treatment values of Y between treatment and control groups

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

Difference-in-Difference Models II

  • The difference-in-difference model (aka "diff-in-diff" or DND") identifies treatment effect by differencing the difference pre- and post-treatment values of Y between treatment and control groups

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

  • Treatedi={1 if i is in treatment group0 if i is not in treatment group

  • Aftert={1 if t is after treatment period0 if t is before treatment period

Difference-in-Difference Models II

  • The difference-in-difference model (aka "diff-in-diff" or DND") identifies treatment effect by differencing the difference pre- and post-treatment values of Y between treatment and control groups

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

  • Treatedi={1 if i is in treatment group0 if i is not in treatment group

  • Aftert={1 if t is after treatment period0 if t is before treatment period

Control Treatment Group Diff (ΔYi)
Before β0 β0+β1 β1
After β0+β2 β0+β1+β2+β3 β1+β3
Time Diff (ΔYt) β2 β2+β3 Diff-in-diff ΔiΔt:β3

Visualizing Diff-in-Diff

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

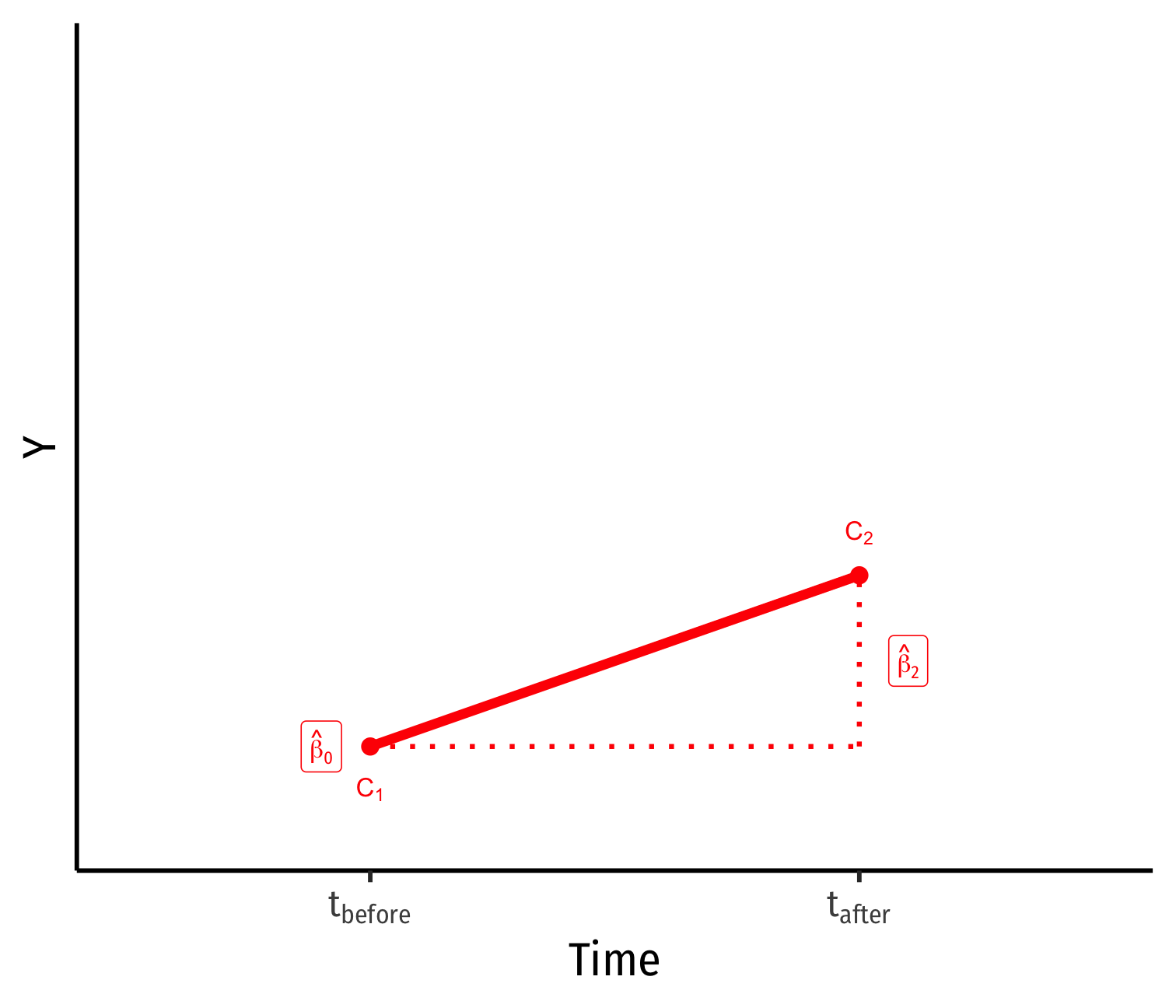
  • Control group (Treated=0)

  • ^β0: value of Y for control group before treatment

  • ^β2: time difference (for control group)

Visualizing Diff-in-Diff

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

  • Control group (Treated=0)

  • ^β0: value of Y for control group before treatment

  • ^β2: time difference (for control group)

  • Treated group (Treated=1)

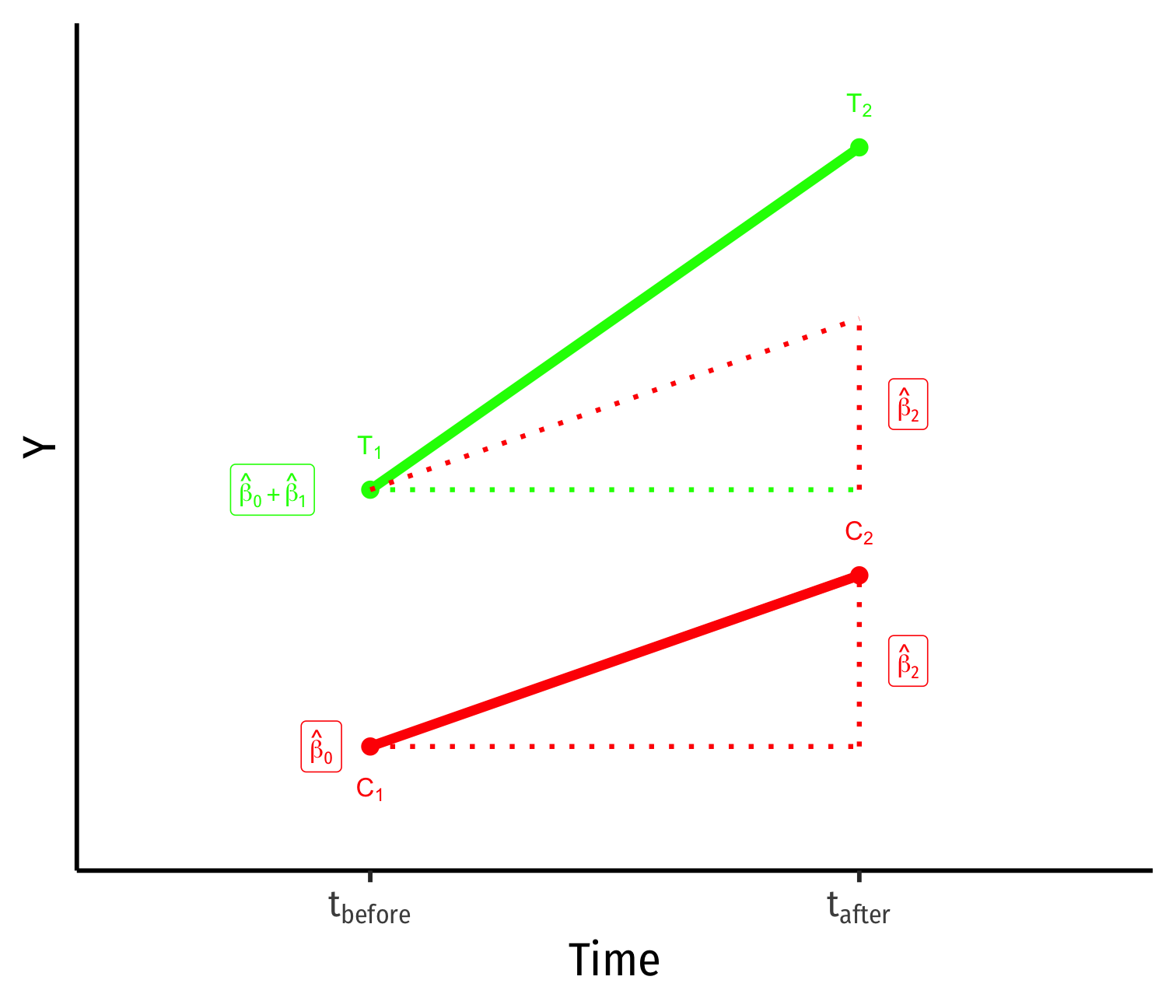
Visualizing Diff-in-Diff

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

  • Control group (Treated=0)

  • ^β0: value of Y for control group before treatment

  • ^β2: time difference (for control group)

  • Treated group (Treated=1)

  • ^β1: difference between groups before treatment

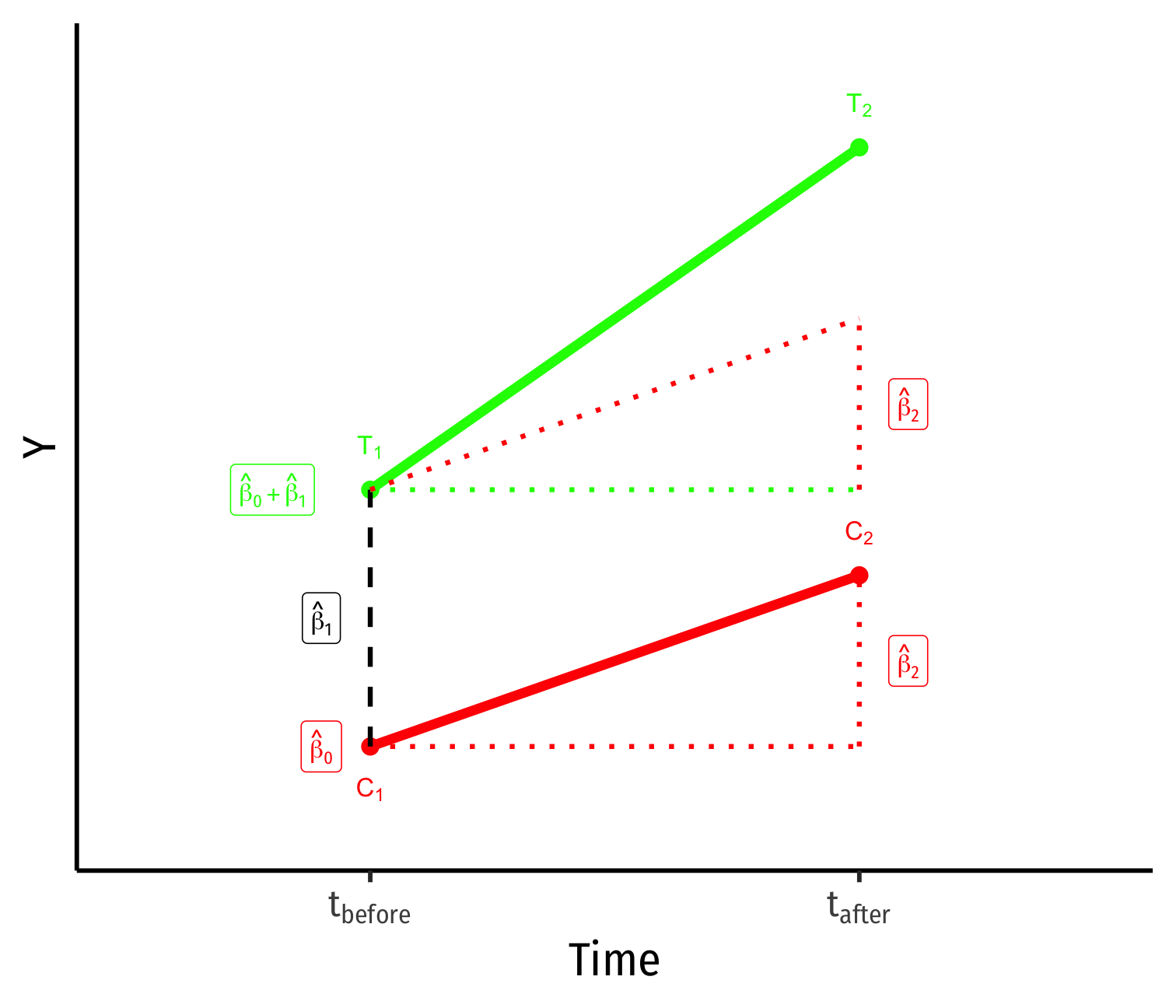
Visualizing Diff-in-Diff

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

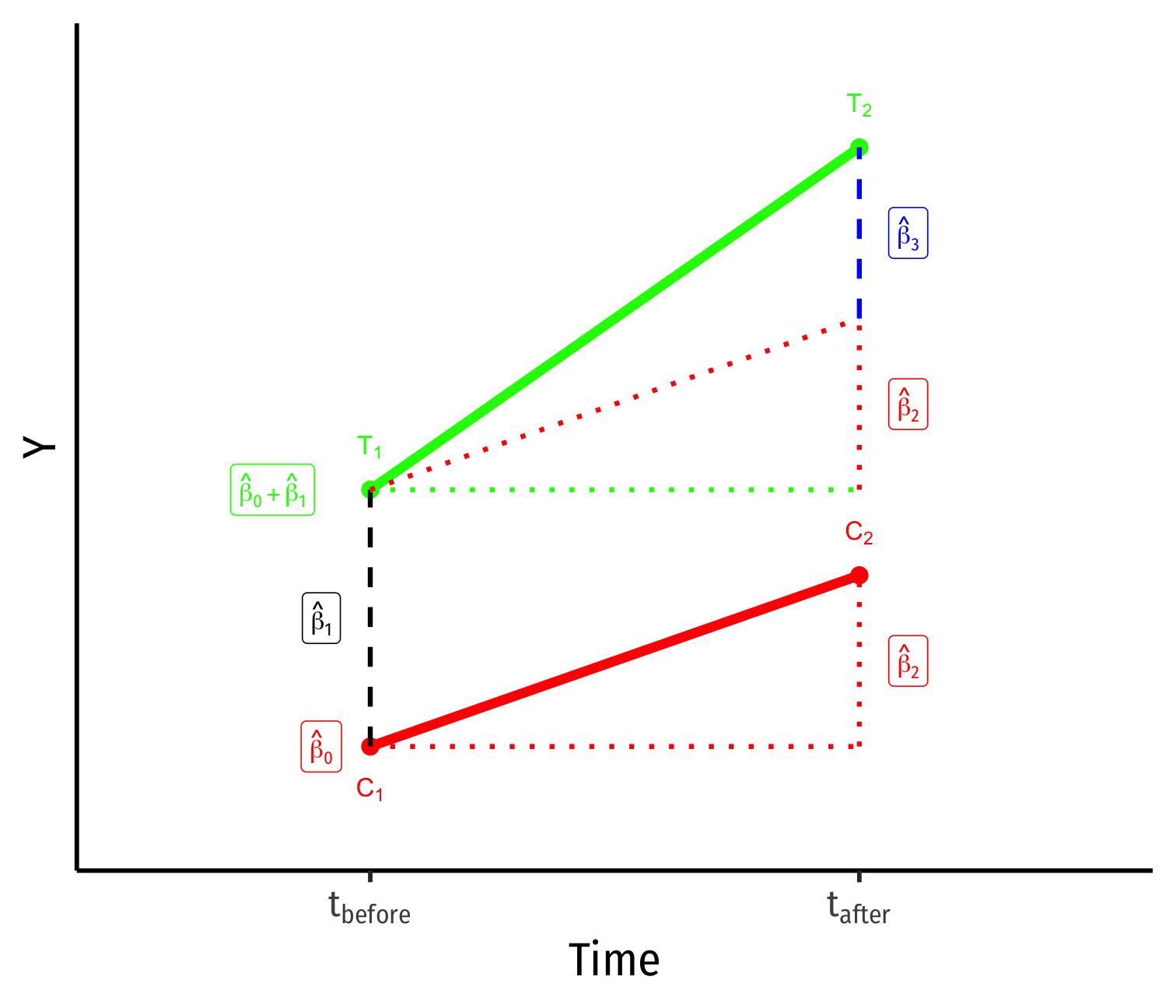
  • Control group (Treated=0)

  • ^β0: value of Y for control group before treatment

  • ^β2: time difference (for control group)

  • Treated group (Treated=1)

  • ^β1: difference between groups before treatment

  • ^β3: difference-in-difference: treatment effect

Visualizing Diff-in-Diff II

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

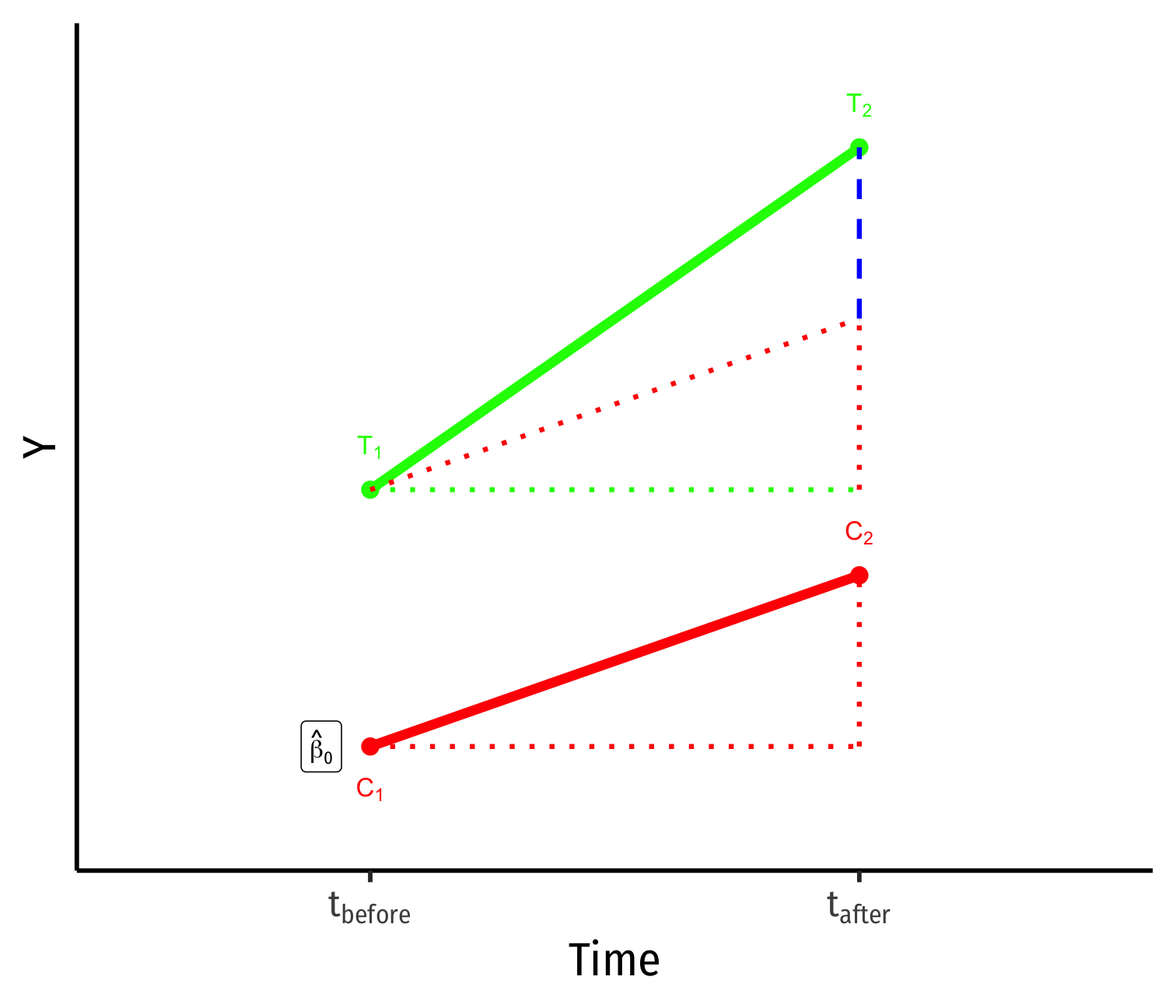
  • Yi for Control group before: ^β0

Visualizing Diff-in-Diff II

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

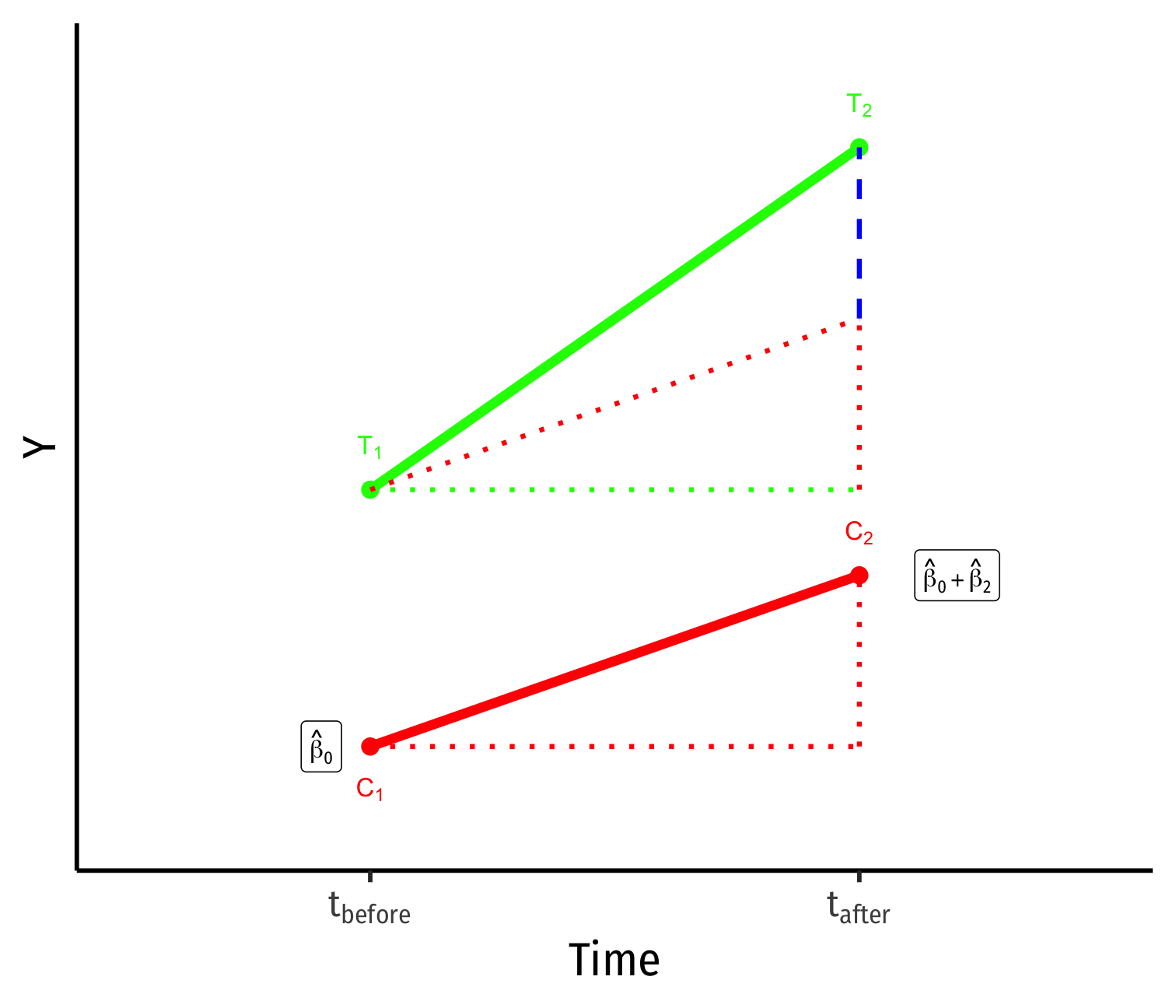
  • Yi for Control group before: ^β0

  • Yi for Control group after: ^β0+^β2

Visualizing Diff-in-Diff II

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

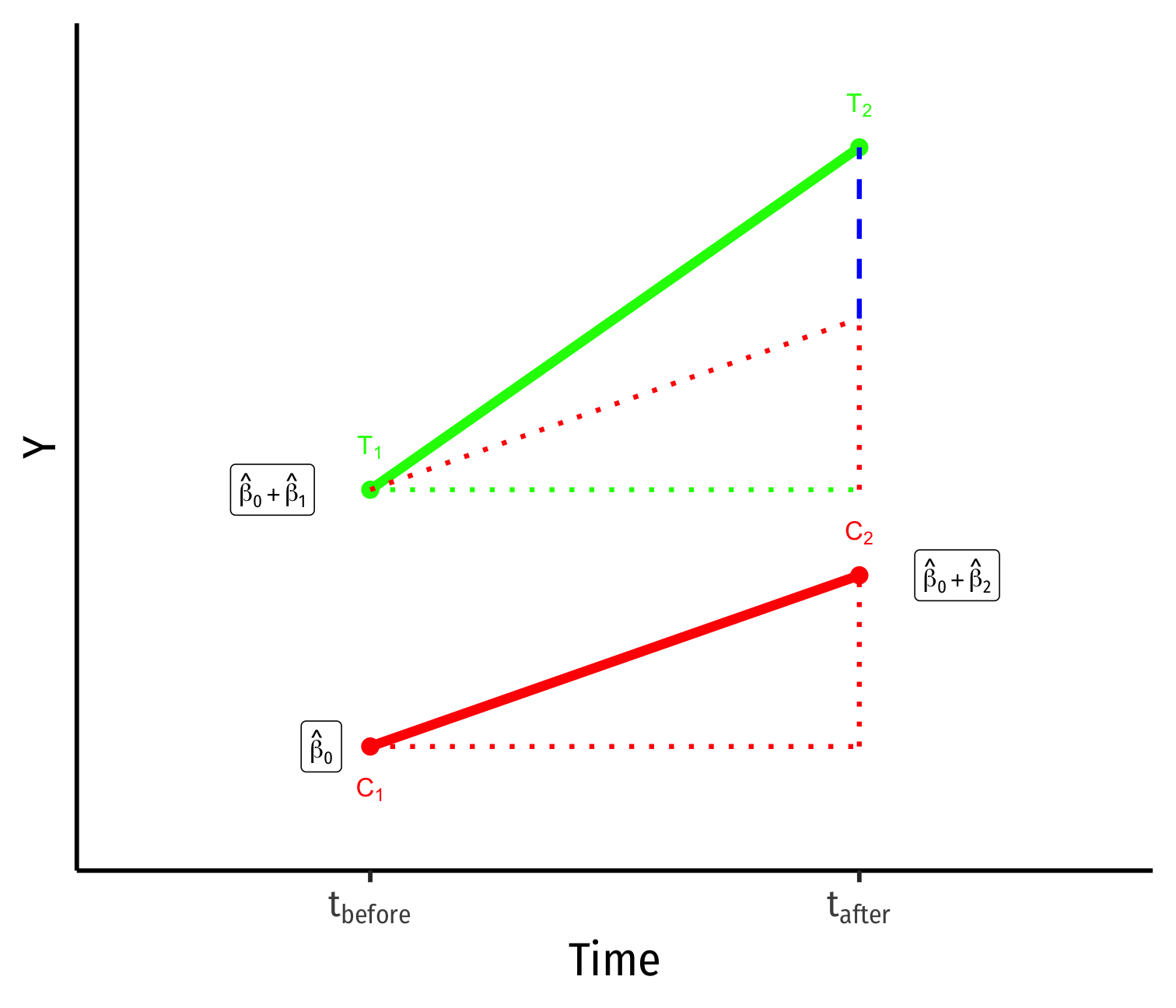
  • Yi for Control group before: ^β0

  • Yi for Control group after: ^β0+^β2

  • Yi for Treatment group before: ^β0+^β1

Visualizing Diff-in-Diff II

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

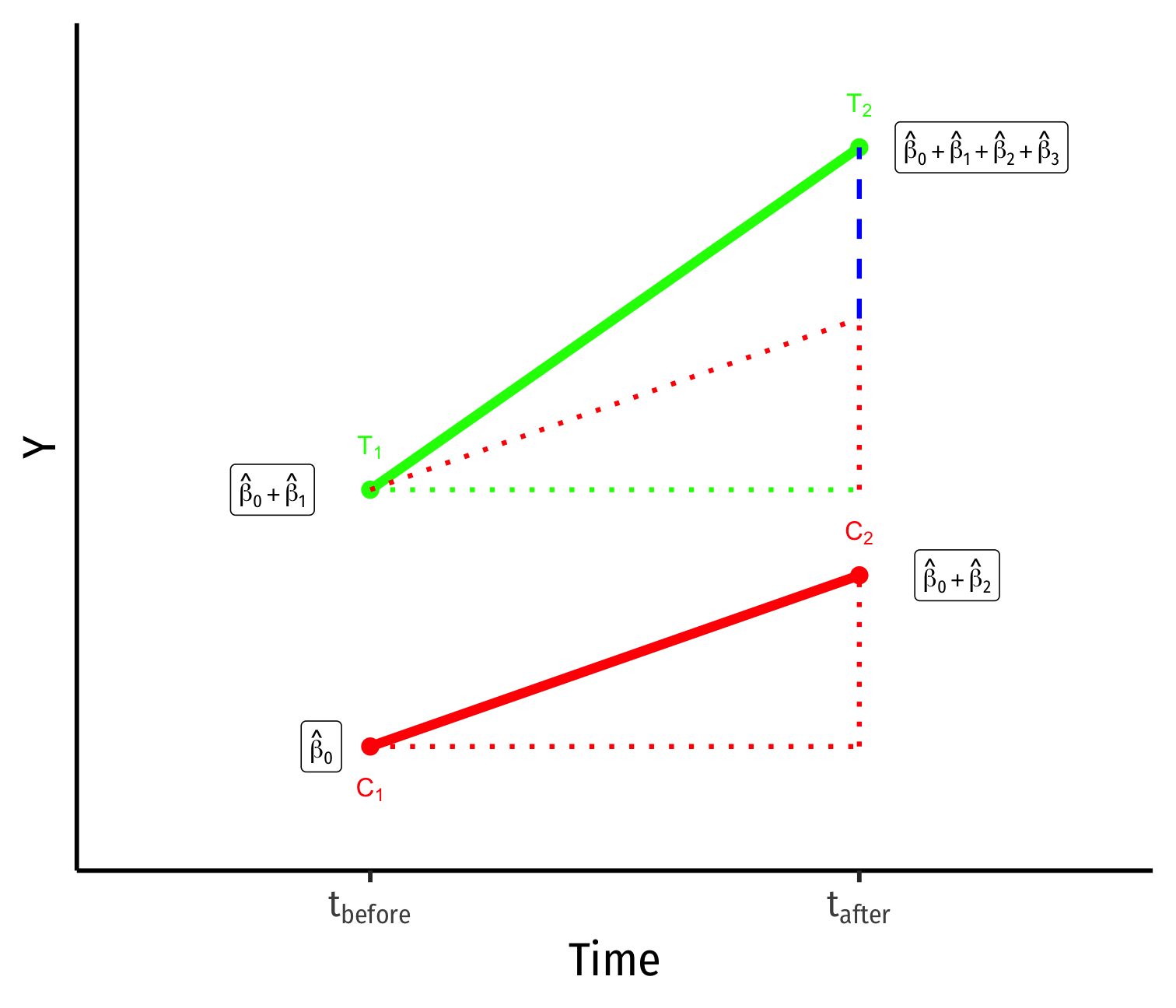
  • Yi for Control group before: ^β0

  • Yi for Control group after: ^β0+^β2

  • Yi for Treatment group before: ^β0+^β1

  • Yi for Treatment group after: ^β0+^β1+^β2+^β3

Visualizing Diff-in-Diff II

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

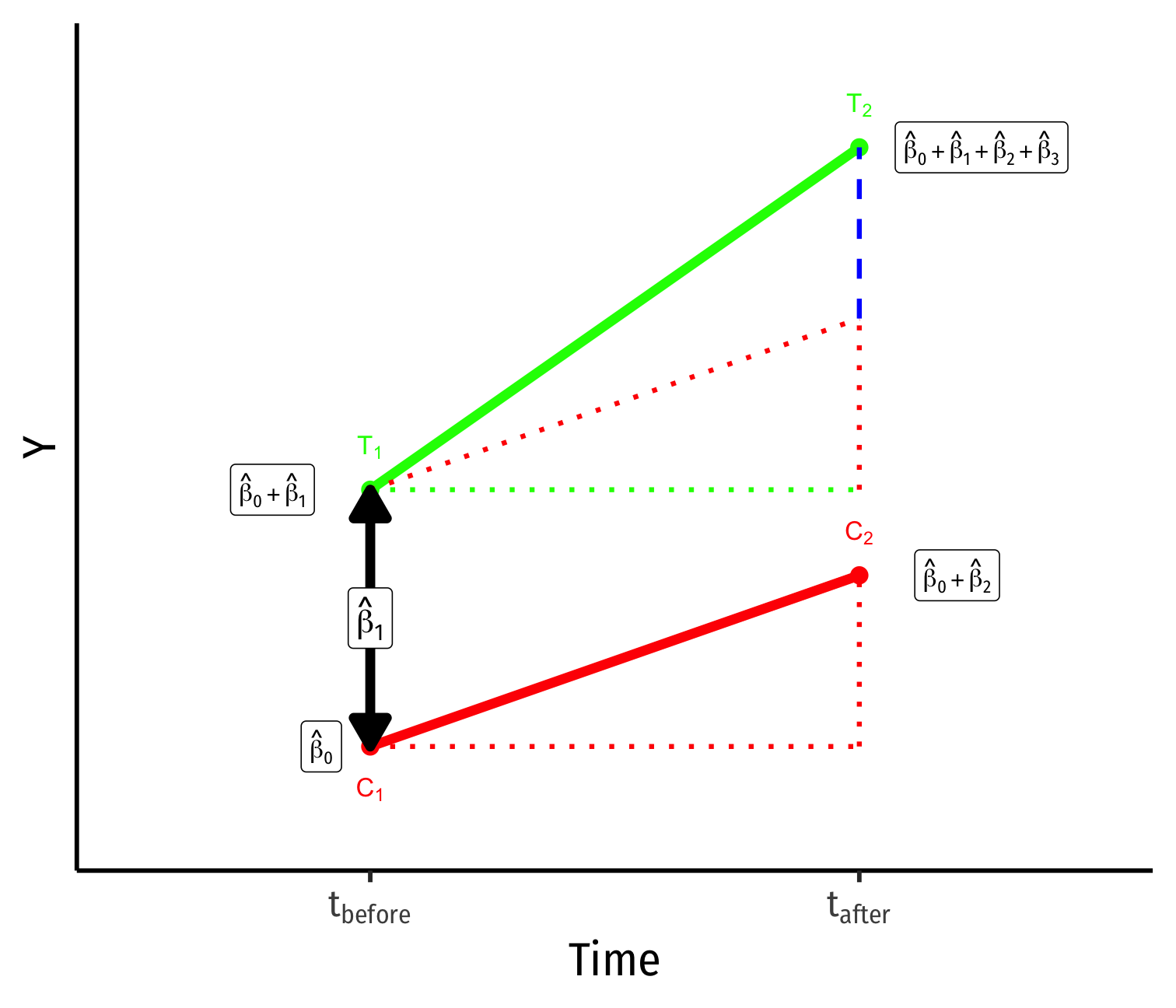
  • Yi for Control group before: ^β0

  • Yi for Control group after: ^β0+^β2

  • Yi for Treatment group before: ^β0+^β1

  • Yi for Treatment group after: ^β0+^β1+^β2+^β3

  • Group Difference (before): ^β1

Visualizing Diff-in-Diff II

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

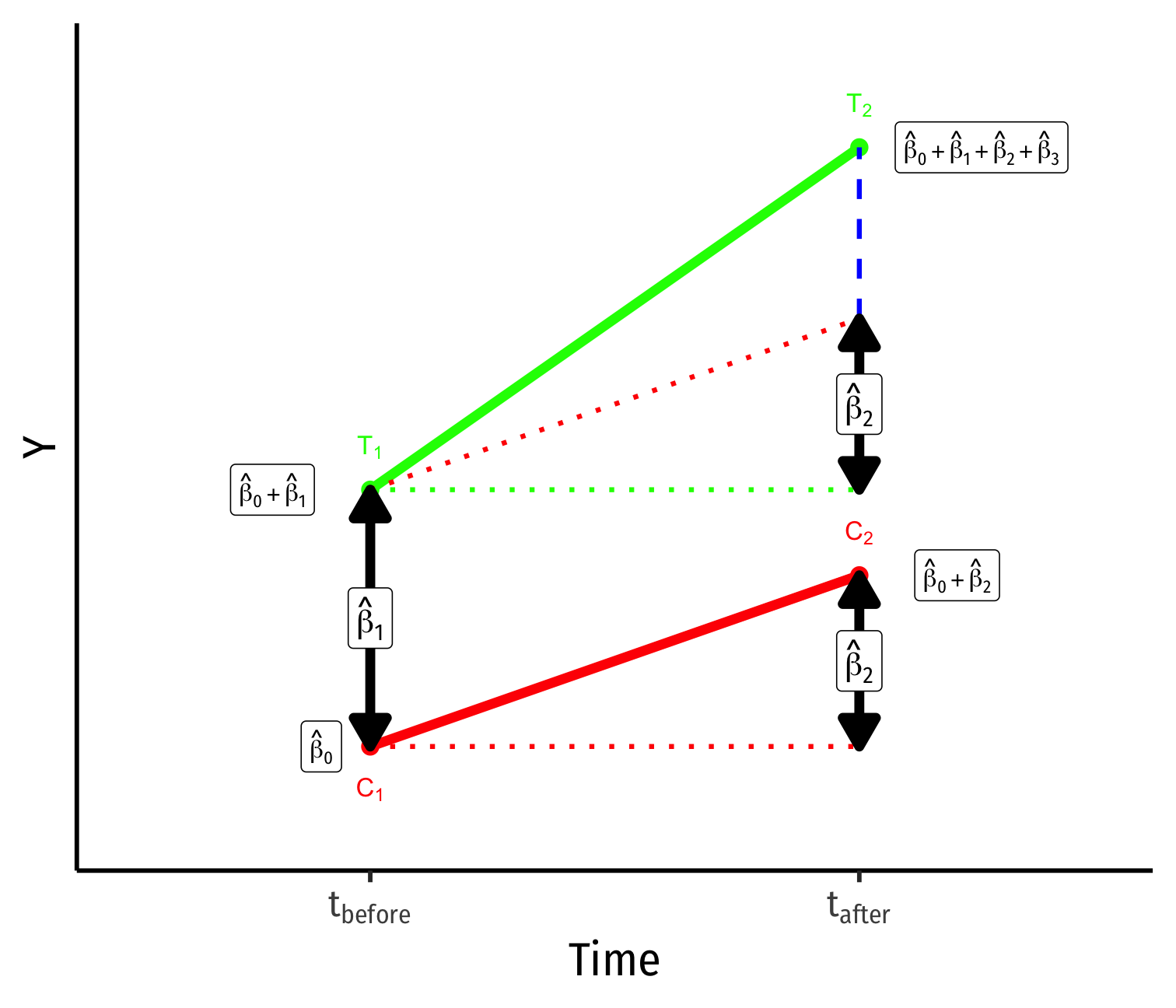
  • Yi for Control group before: ^β0

  • Yi for Control group after: ^β0+^β2

  • Yi for Treatment group before: ^β0+^β1

  • Yi for Treatment group after: ^β0+^β1+^β2+^β3

  • Group Difference (before): ^β1

  • Time Difference: ^β2

Visualizing Diff-in-Diff II

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

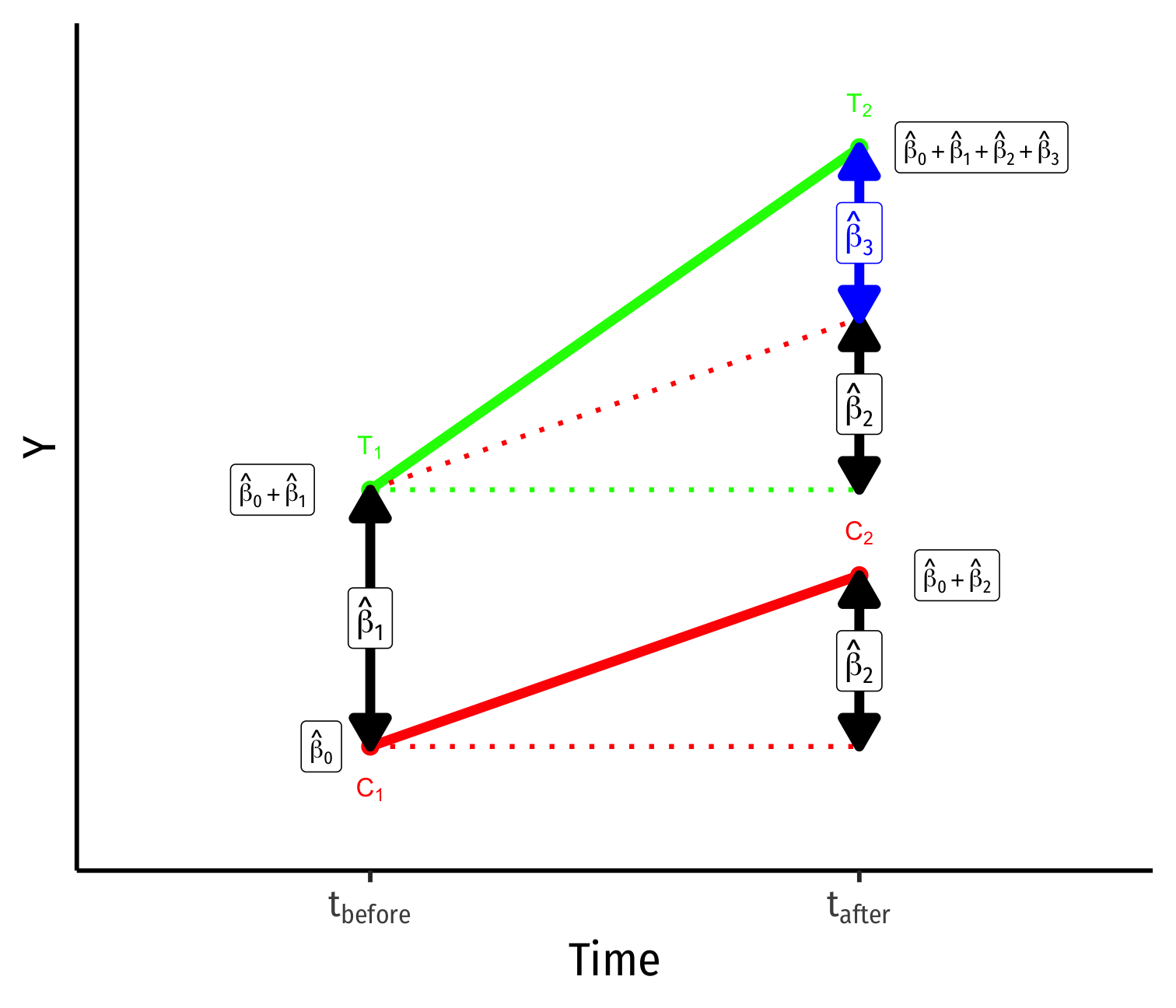
  • Yi for Control group before: ^β0

  • Yi for Control group after: ^β0+^β2

  • Yi for Treatment group before: ^β0+^β1

  • Yi for Treatment group after: ^β0+^β1+^β2+^β3

  • Group Difference (before): ^β1

  • Time Difference: ^β2

  • Difference-in-difference: ^β3 (treatment effect)

Comparing Group Means (Again)

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

Control Treatment Group Diff (ΔYi)
Before β0 β0+β1 β1
After β0+β2 β0+β1+β2+β3 β1+β3
Time Diff (ΔYt) β2 β2+β3 Diff-in-diff ΔiΔt:β3

Key Assumption: Counterfactual

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

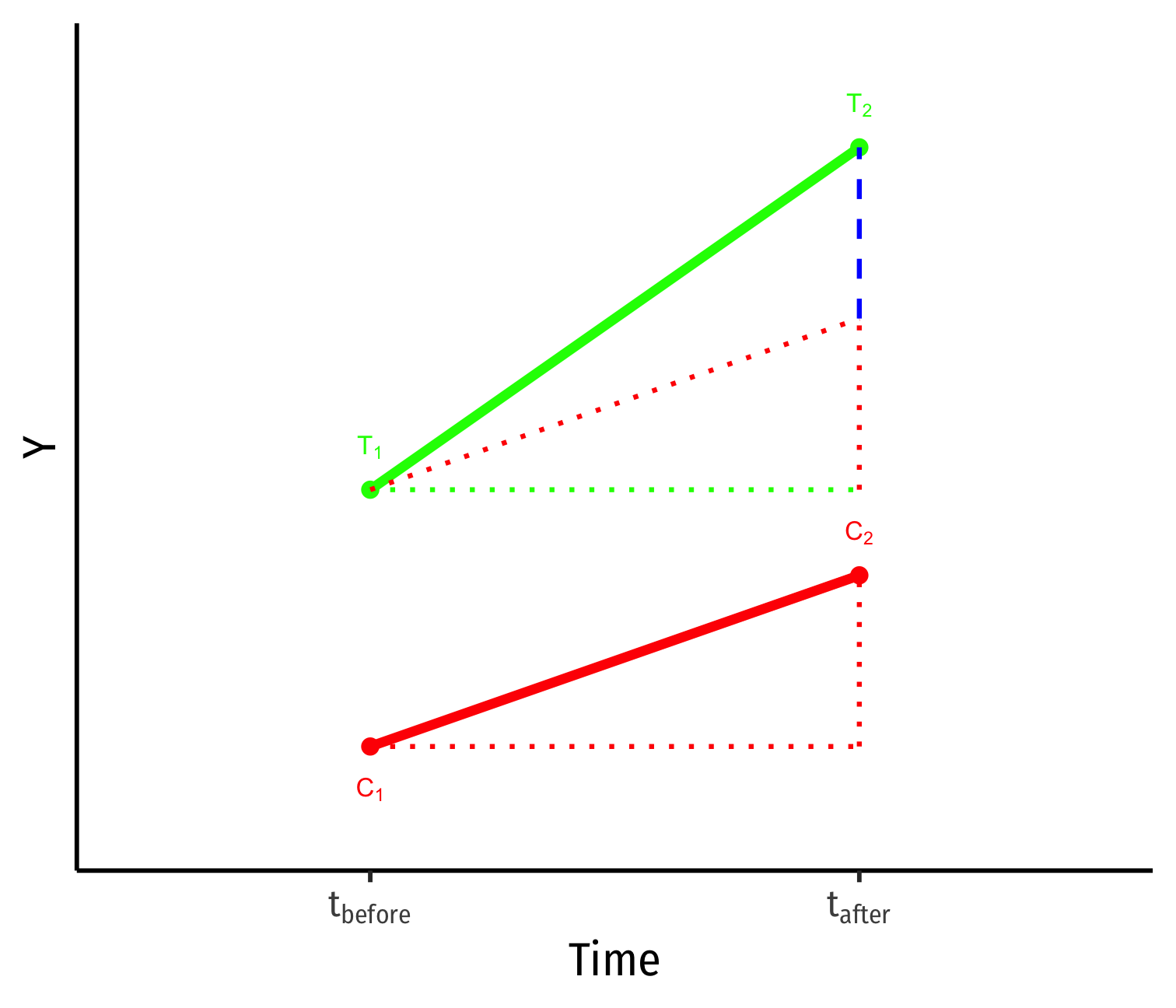
  • Key assumption for DND: time trends (for treatment and control) are parallel

  • Treatment and control groups assumed to be identical over time on average, except for treatment

  • Counterfactual: if the treatment group had not recieved treatment, it would have changed identically over time as the control group (^β2)

Key Assumption: Counterfactual

^Yit=β0+β1Treatedi+β2Aftert+β3(Treatedi×Aftert)+uit

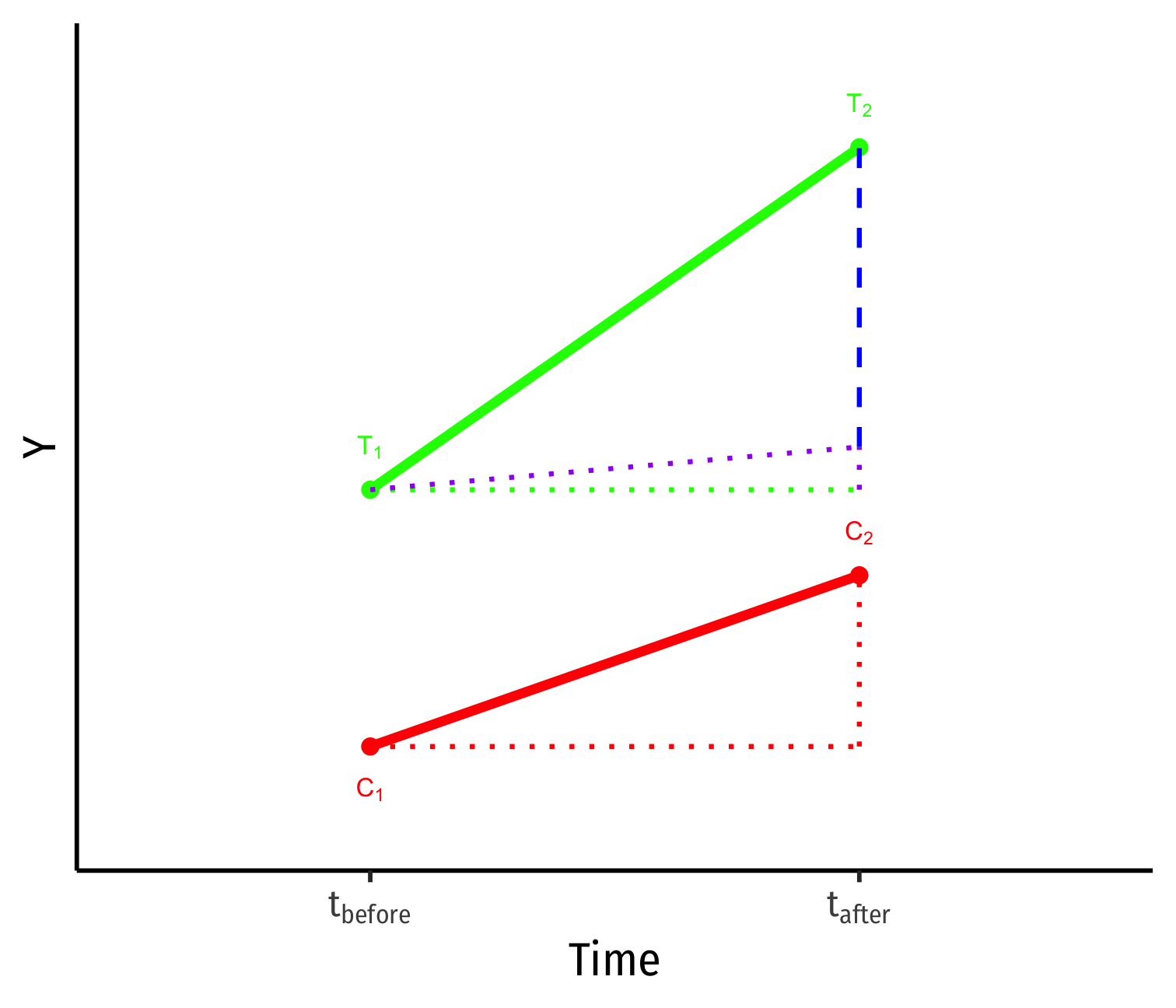
  • If the time-trends would have been different, a biased measure of the treatment effect (^β3)!

Diff-in-Diff Example I

Example: In 1993 Georgia initiated a HOPE scholarship program to let state residents with at least a B average in high school attend public college in Georgia for free. Did it increase college enrollment?

  • Micro-level data on 4,291 young individuals

Diff-in-Diff Example I

Example: In 1993 Georgia initiated a HOPE scholarship program to let state residents with at least a B average in high school attend public college in Georgia for free. Did it increase college enrollment?

  • Micro-level data on 4,291 young individuals

  • InCollegeit={1 if i is in college during year t0 if i is not in college during year t

Diff-in-Diff Example I

Example: In 1993 Georgia initiated a HOPE scholarship program to let state residents with at least a B average in high school attend public college in Georgia for free. Did it increase college enrollment?

  • Micro-level data on 4,291 young individuals

  • InCollegeit={1 if i is in college during year t0 if i is not in college during year t

  • Georgiai={1 if i is a Georgia resident0 if i is not a Georgia resident

Diff-in-Diff Example I

Example: In 1993 Georgia initiated a HOPE scholarship program to let state residents with at least a B average in high school attend public college in Georgia for free. Did it increase college enrollment?

  • Micro-level data on 4,291 young individuals

  • InCollegeit={1 if i is in college during year t0 if i is not in college during year t

  • Georgiai={1 if i is a Georgia resident0 if i is not a Georgia resident

  • Aftert={1 if t is after 19920 if t is after 1992

Dynarski, Susan (2000), "Hope for Whom? Financial Aid for the Middle Class and Its Impact on College Attendance"

Note: With a dummy dependent (Y) variable, coefficients estimate the probability Y=1, i.e. the probability a person is enrolled in college

Diff-in-Diff Example II

  • We can use a DND model to measure the effect of HOPE scholarship on enrollments

  • Georgia and nearby States, if not for HOPE, changes should be the same over time

Diff-in-Diff Example II

  • We can use a DND model to measure the effect of HOPE scholarship on enrollments

  • Georgia and nearby States, if not for HOPE, changes should be the same over time

  • Treatment period: after 1992

Diff-in-Diff Example II

  • We can use a DND model to measure the effect of HOPE scholarship on enrollments

  • Georgia and nearby States, if not for HOPE, changes should be the same over time

  • Treatment period: after 1992

  • Treatment: Georgia

Diff-in-Diff Example II

  • We can use a DND model to measure the effect of HOPE scholarship on enrollments

  • Georgia and nearby States, if not for HOPE, changes should be the same over time

  • Treatment period: after 1992

  • Treatment: Georgia

  • Differences-in-differences: ΔiΔtEnrolled=(GAafter−GAbefore)−(neighborsafter−neighborsbefore)

Diff-in-Diff Example II

  • We can use a DND model to measure the effect of HOPE scholarship on enrollments

  • Georgia and nearby States, if not for HOPE, changes should be the same over time

  • Treatment period: after 1992

  • Treatment: Georgia

  • Differences-in-differences: ΔiΔtEnrolled=(GAafter−GAbefore)−(neighborsafter−neighborsbefore)

  • Regression equation: ^Enrolledit=β0+β1Georgiai+β2Aftert+β3(Georgiai×Aftert)

Example: Regression

DND_reg<-lm(InCollege ~ Georgia + After + Georgia:After, data = hope)
summary(DND_reg)
## 
## Call:
## lm(formula = InCollege ~ Georgia + After + Georgia:After, data = hope)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4058 -0.4058 -0.4013  0.5942  0.6995 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    0.40578    0.01092  37.146  < 2e-16 ***
## Georgia       -0.10524    0.03778  -2.785  0.00537 ** 
## After         -0.00446    0.01585  -0.281  0.77848    
## Georgia:After  0.08933    0.04889   1.827  0.06776 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4893 on 4287 degrees of freedom
## Multiple R-squared:  0.001872,    Adjusted R-squared:  0.001174 
## F-statistic: 2.681 on 3 and 4287 DF,  p-value: 0.04528

Example: Regression

DND_reg<-lm(InCollege ~ Georgia + After + Georgia:After, data = hope)
summary(DND_reg)
## 
## Call:
## lm(formula = InCollege ~ Georgia + After + Georgia:After, data = hope)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4058 -0.4058 -0.4013  0.5942  0.6995 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    0.40578    0.01092  37.146  < 2e-16 ***
## Georgia       -0.10524    0.03778  -2.785  0.00537 ** 
## After         -0.00446    0.01585  -0.281  0.77848    
## Georgia:After  0.08933    0.04889   1.827  0.06776 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4893 on 4287 degrees of freedom
## Multiple R-squared:  0.001872,    Adjusted R-squared:  0.001174 
## F-statistic: 2.681 on 3 and 4287 DF,  p-value: 0.04528

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • β0:

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • β0: A non-Georgian before 1992 was 40.6% likely to be a college student

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • β0: A non-Georgian before 1992 was 40.6% likely to be a college student

  • β1:

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • β0: A non-Georgian before 1992 was 40.6% likely to be a college student

  • β1: Georgians before 1992 were 10.5% less likely to be college students than neighboring states

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • β0: A non-Georgian before 1992 was 40.6% likely to be a college student

  • β1: Georgians before 1992 were 10.5% less likely to be college students than neighboring states

  • β2:

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • β0: A non-Georgian before 1992 was 40.6% likely to be a college student

  • β1: Georgians before 1992 were 10.5% less likely to be college students than neighboring states

  • β2: After 1992, non-Georgians are 0.4% less likely to be college students

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • β0: A non-Georgian before 1992 was 40.6% likely to be a college student

  • β1: Georgians before 1992 were 10.5% less likely to be college students than neighboring states

  • β2: After 1992, non-Georgians are 0.4% less likely to be college students

  • β3:

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • β0: A non-Georgian before 1992 was 40.6% likely to be a college student

  • β1: Georgians before 1992 were 10.5% less likely to be college students than neighboring states

  • β2: After 1992, non-Georgians are 0.4% less likely to be college students

  • β3: After 1992, Georgians are 8.9% more likely to enroll in colleges than neighboring states

Example: Interpretting the Regression

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • β0: A non-Georgian before 1992 was 40.6% likely to be a college student

  • β1: Georgians before 1992 were 10.5% less likely to be college students than neighboring states

  • β2: After 1992, non-Georgians are 0.4% less likely to be college students

  • β3: After 1992, Georgians are 8.9% more likely to enroll in colleges than neighboring states

  • Treatment effect: HOPE increased enrollment likelihood by 8.9%

Example: Comparing Group Means

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • A group mean for a dummy Y is E[Y=1], i.e. the probability a student is enrolled:

  • Non-Georgian enrollment probability pre-1992:

Example: Comparing Group Means

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • A group mean for a dummy Y is E[Y=1], i.e. the probability a student is enrolled:

  • Non-Georgian enrollment probability pre-1992: β0=0.406

Example: Comparing Group Means

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • A group mean for a dummy Y is E[Y=1], i.e. the probability a student is enrolled:

  • Non-Georgian enrollment probability pre-1992: β0=0.406

  • Georgian enrollment probability pre-1992:

Example: Comparing Group Means

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • A group mean for a dummy Y is E[Y=1], i.e. the probability a student is enrolled:

  • Non-Georgian enrollment probability pre-1992: β0=0.406

  • Georgian enrollment probability pre-1992: β0+β1=0.406−0.105=0.301

Example: Comparing Group Means

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • A group mean for a dummy Y is E[Y=1], i.e. the probability a student is enrolled:

  • Non-Georgian enrollment probability pre-1992: β0=0.406

  • Georgian enrollment probability pre-1992: β0+β1=0.406−0.105=0.301

  • Non-Georgian enrollment probability post-1992:

Example: Comparing Group Means

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • A group mean for a dummy Y is E[Y=1], i.e. the probability a student is enrolled:

  • Non-Georgian enrollment probability pre-1992: β0=0.406

  • Georgian enrollment probability pre-1992: β0+β1=0.406−0.105=0.301

  • Non-Georgian enrollment probability post-1992: β0+β2=0.406−0.004=0.402

Example: Comparing Group Means

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • A group mean for a dummy Y is E[Y=1], i.e. the probability a student is enrolled:

  • Non-Georgian enrollment probability pre-1992: β0=0.406

  • Georgian enrollment probability pre-1992: β0+β1=0.406−0.105=0.301

  • Non-Georgian enrollment probability post-1992: β0+β2=0.406−0.004=0.402

  • Georgian enrollment probability post-1992:

Example: Comparing Group Means

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

  • A group mean for a dummy Y is E[Y=1], i.e. the probability a student is enrolled:

  • Non-Georgian enrollment probability pre-1992: β0=0.406

  • Georgian enrollment probability pre-1992: β0+β1=0.406−0.105=0.301

  • Non-Georgian enrollment probability post-1992: β0+β2=0.406−0.004=0.402

  • Georgian enrollment probability post-1992: β0+β1+β2+β3=0.406−0.105−0.004+0.089=0.386

Example: Comparing Group Means in R

# group mean for non-Georgian before 1992
hope %>%
  filter(Georgia==0,
         After==0) %>%
  summarize(prob = mean(InCollege))
ABCDEFGHIJ0123456789
prob
<dbl>
0.4057827
1 row

Example: Comparing Group Means in R

# group mean for non-Georgian before 1992
hope %>%
  filter(Georgia==0,
         After==0) %>%
  summarize(prob = mean(InCollege))
ABCDEFGHIJ0123456789
prob
<dbl>
0.4057827
1 row
# group mean for non-Georgian AFTER 1992
hope %>%
  filter(Georgia==0,
         After==1) %>%
  summarize(prob = mean(InCollege))
ABCDEFGHIJ0123456789
prob
<dbl>
0.401323
1 row

Example: Comparing Group Means in R II

# group mean for Georgian before 1992
hope %>%
  filter(Georgia==1,
         After==0) %>%
  summarize(prob = mean(InCollege))
ABCDEFGHIJ0123456789
prob
<dbl>
0.3005464
1 row

Example: Comparing Group Means in R II

# group mean for Georgian before 1992
hope %>%
  filter(Georgia==1,
         After==0) %>%
  summarize(prob = mean(InCollege))
ABCDEFGHIJ0123456789
prob
<dbl>
0.3005464
1 row
# group mean for Georgian AFTER 1992
hope %>%
  filter(Georgia==1,
         After==1) %>%
  summarize(prob = mean(InCollege))
ABCDEFGHIJ0123456789
prob
<dbl>
0.3854167
1 row

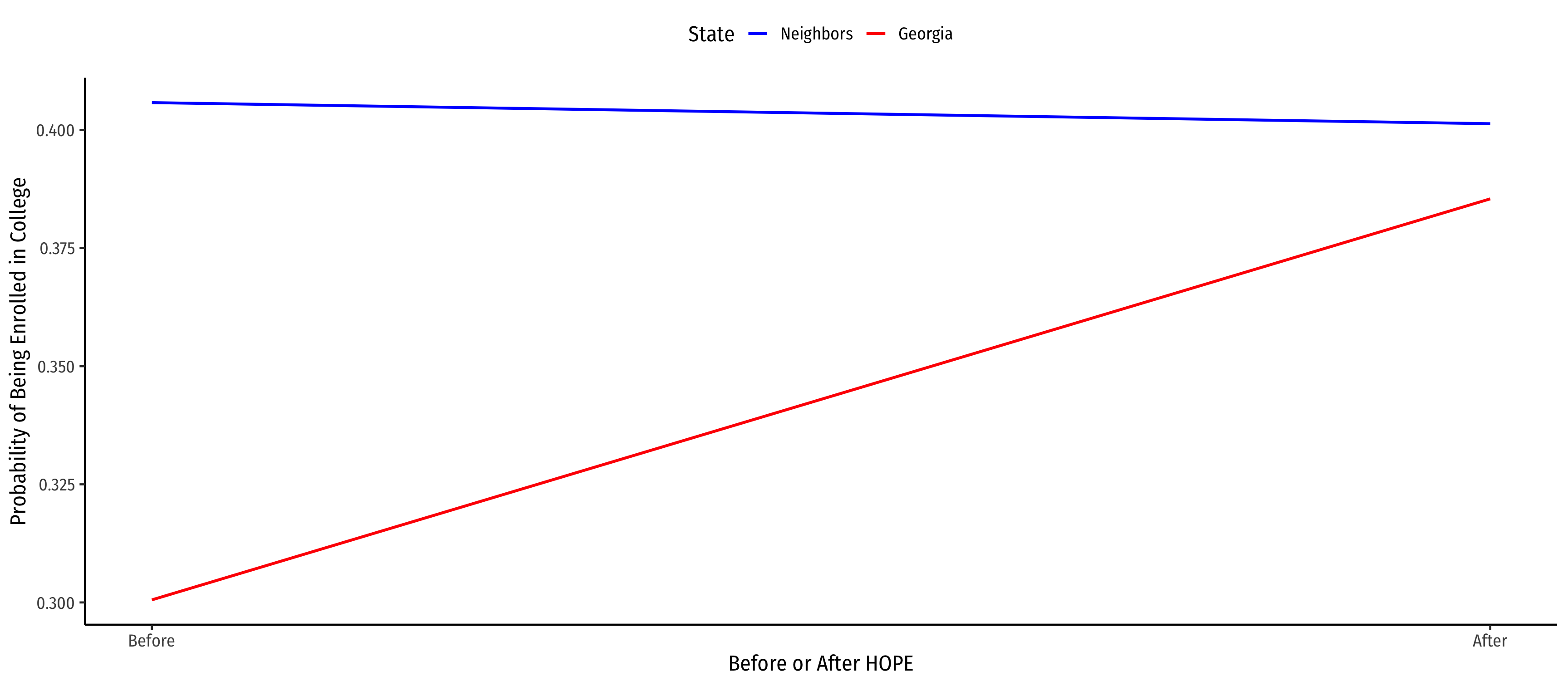
Example: Diff-in-Diff Summary

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

Neighbors Georgia Group Diff (ΔYi)
Before 0.406 0.301 −0.105
After 0.402 0.386 0.016
Time Diff (ΔYt) −0.004 0.085 Diff-in-diff: 0.089

Example: Diff-in-Diff Summary

^Enrolledit=0.406−0.105Georgiai−0.004Aftert+0.089(Georgiai×Aftert)

Neighbors Georgia Group Diff (ΔYi)
Before 0.406 0.301 −0.105
After 0.402 0.386 0.016
Time Diff (ΔYt) −0.004 0.085 Diff-in-diff: 0.089

ΔiΔtEnrolled=(GAafter−GAbefore)−(neighborsafter−neighborsbefore)=(0.386−0.301)−(0.402−0.406)=(0.085)−(−0.004)=0.089

Example: Diff-in-Diff Graph

Generalizing DND Models

Generalizing DND Models

  • DND can be generalized with a two-way fixed effects model:
    ^Yit=αi+θt+β3(Treatedi∗Aftert)+νit
    • αi: group fixed effects (treatments/control groups)
    • θt: time fixed effects (pre/post treatment)

Generalizing DND Models

  • DND can be generalized with a two-way fixed effects model:
    ^Yit=αi+θt+β3(Treatedi∗Aftert)+νit
    • αi: group fixed effects (treatments/control groups)
    • θt: time fixed effects (pre/post treatment)
  • Allows many periods, and treatment(s) can occur at different times to different units (so long as some do not get treated)

Generalizing DND Models

  • DND can be generalized with a two-way fixed effects model:
    ^Yit=αi+θt+β3(Treatedi∗Aftert)+νit
    • αi: group fixed effects (treatments/control groups)
    • θt: time fixed effects (pre/post treatment)

  • Allows many periods, and treatment(s) can occur at different times to different units (so long as some do not get treated)

  • Can also add control variables that vary within units and over time ^Yit=αi+θt+β3(Treatedi×Aftert)+β4Xit+νit

Our Example, Generalized I

^Enrolledit=αi+θt+β3(Georgiait×Afterit)

  • StateCode is a variable for the State ⟹ create State fixed effect

  • Year is a variable for the year ⟹ create year fixed effect

  • Using LSDV method... 

DND_fe<-lm(InCollege ~ Georgia:After + factor(StateCode) + factor(Year),
           data = hope)
summary(DND_fe)

Our Example, Generalized II

## 
## Call:
## lm(formula = InCollege ~ Georgia:After + factor(StateCode) + 
##     factor(Year), data = hope)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4934 -0.4148 -0.3344  0.5690  0.7359 
## 
## Coefficients:
##                      Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          0.418057   0.022611  18.489  < 2e-16 ***
## factor(StateCode)57 -0.014181   0.027397  -0.518 0.604754    
## factor(StateCode)58 -0.141501   0.039361  -3.595 0.000328 ***
## factor(StateCode)59 -0.062379   0.019543  -3.192 0.001424 ** 
## factor(StateCode)62 -0.132650   0.028061  -4.727 2.35e-06 ***
## factor(StateCode)63 -0.005104   0.026278  -0.194 0.846007    
## factor(Year)90       0.046609   0.028336   1.645 0.100075    
## factor(Year)91       0.032276   0.028569   1.130 0.258642    
## factor(Year)92       0.023536   0.029846   0.789 0.430403    
## factor(Year)93       0.030161   0.030154   1.000 0.317254    
## factor(Year)94       0.014505   0.030574   0.474 0.635220    
## factor(Year)95      -0.003263   0.031699  -0.103 0.918007    
## factor(Year)96      -0.021314   0.032263  -0.661 0.508883    
## factor(Year)97       0.075341   0.031280   2.409 0.016057 *  
## Georgia:After        0.091420   0.048761   1.875 0.060879 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4875 on 4276 degrees of freedom
## Multiple R-squared:  0.01146,    Adjusted R-squared:  0.008222 
## F-statistic:  3.54 on 14 and 4276 DF,  p-value: 7.84e-06

Our Example, Generalized II

## 
## Call:
## lm(formula = InCollege ~ Georgia:After + factor(StateCode) + 
##     factor(Year), data = hope)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4934 -0.4148 -0.3344  0.5690  0.7359 
## 
## Coefficients:
##                      Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          0.418057   0.022611  18.489  < 2e-16 ***
## factor(StateCode)57 -0.014181   0.027397  -0.518 0.604754    
## factor(StateCode)58 -0.141501   0.039361  -3.595 0.000328 ***
## factor(StateCode)59 -0.062379   0.019543  -3.192 0.001424 ** 
## factor(StateCode)62 -0.132650   0.028061  -4.727 2.35e-06 ***
## factor(StateCode)63 -0.005104   0.026278  -0.194 0.846007    
## factor(Year)90       0.046609   0.028336   1.645 0.100075    
## factor(Year)91       0.032276   0.028569   1.130 0.258642    
## factor(Year)92       0.023536   0.029846   0.789 0.430403    
## factor(Year)93       0.030161   0.030154   1.000 0.317254    
## factor(Year)94       0.014505   0.030574   0.474 0.635220    
## factor(Year)95      -0.003263   0.031699  -0.103 0.918007    
## factor(Year)96      -0.021314   0.032263  -0.661 0.508883    
## factor(Year)97       0.075341   0.031280   2.409 0.016057 *  
## Georgia:After        0.091420   0.048761   1.875 0.060879 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4875 on 4276 degrees of freedom
## Multiple R-squared:  0.01146,    Adjusted R-squared:  0.008222 
## F-statistic:  3.54 on 14 and 4276 DF,  p-value: 7.84e-06

^InCollegeit=αi+θt+0.091(Georgiai×Afterit)

Intuition behind DND

  • Diff-in-diff models are the quintessential example of exploiting natural experiments

  • A major change at a point in time (change in law, a natural disaster, political crisis) separates groups where one is affected and another is not---identifies the effect of the change (treatment)

  • One of the cleanest and clearest causal identification strategies

Example: "The" Card-Kreuger Minimum Wage Study

Example: "The" Card-Kreuger Minimum Wage Study I

Example: The controversial minimum wage study, Card & Kreuger (1994) is a quintessential (and clever) diff-in-diff.

Card, David, Krueger, Alan B, (1994), "Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania," American Economic Review 84 (4): 772–793

Card & Kreuger (1994): Background I

  • Card & Kreuger (1994) compare employment in fast food restaurants on New Jersey and Pennsylvania sides of border between February and November 1992.

  • Pennsylvania & New Jersey both had a minimum wage of $4.25 before February 1992

  • In February 1992, New Jersey raised minimum wage from $4.25 to $5.05

Card & Kreuger (1994): Background II

  • If we look only at New Jersey before & after change:

    • Omitted variable bias: macroeconomic variables (there's a recession!), weather, etc.
    • Including PA as a control will control for these time-varying effects if they are national trends

  • Surveyed 400 fast food restaurants on each side of the border, before & after min wage increase

    • Key assumption: Pennsylvania and New Jersey follow parallel trends,
    • Counterfactual: if not for the minimum wage increase, NJ employment would have changed similar to PA employment

Card & Kreuger (1994): Comparisons

Card & Kreuger (1994): Summary I

Card & Kreuger (1994): Summary II

Card & Kreuger (1994): Identification Strategy and Model

^Employmentit=β0+β1NJi+β2Aftert+β3(NJi×Aftert)

  • PA Before: β0

  • PA After: β0+β2

  • NJ Before: β0+β1

  • NJ After: β0+β1+β2+β3

  • Diff-in-diff: (NJafter−NJbefore)−(PAafter−PAbefore)

Card & Kreuger (1994): Identification Strategy and Model

^Employmentit=β0+β1NJi+β2Aftert+β3(NJi×Aftert)

  • PA Before: β0

  • PA After: β0+β2

  • NJ Before: β0+β1

  • NJ After: β0+β1+β2+β3

  • Diff-in-diff: (NJafter−NJbefore)−(PAafter−PAbefore)

PA NJ Group Diff (ΔYi)
Before β0 β0+β1 β1
After β0+β2 β0+β1+β2+β3 β1+β3
Time Diff (ΔYt) β2 β2+β3 Diff-in-diff ΔiΔt:β3

Card & Kreuger (1994): Results

Clever Research Designs Identify Causality

Again, this toolkit of research designs to identify causal effects is the economist's comparative advantage that firms and governments want!

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow