+ - 0:00:00
Notes for current slide
Notes for next slide

3.6: Regression with Categorical Data

ECON 480 · Econometrics · Fall 2019

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsf19
metricsF19.classes.ryansafner.com

Categorical Data

  • Categorical data place an individual into one of several possible categories

    • e.g. sex, season, political party
    • may be responses to survey questions
    • can be quantitative (e.g. age, zip code)

  • R calls these factors (we'll deal with them much later in the course)

Example Research Question

Example: do men earn higher wages, on average, than women? If so, how much?

The Pure Statistics of Comparing Group Means

  • Using basic statistics, we can test for a statistically significant difference in group means with a t-test1

  • Define:

  • YM: average earnings of a sample of nM men

  • YW: average earnings of a sample of nW women

  • Difference in group averages: d= ˉYM − ˉYW

  • The hypothesis test is:

    • H0:d=0
    • H1:d≠0

1 See today's class notes page for this example

Comparing Groups with Regression

  • In a regression, we can easily compare across groups via a dummy variable1

  • Dummy variable only =0 or =1, depending on if a condition is met

  • Signifies whether an observation belongs to a category or not

1 Also called a binary variable or dichotomous variable

Comparing Groups with Regression

  • In a regression, we can easily compare across groups via a dummy variable1

  • Dummy variable only =0 or =1, depending on if a condition is met

  • Signifies whether an observation belongs to a category or not

1 Also called a binary variable or dichotomous variable

Example:

^Wagei=^β0+^β1Femalei where Femalei={1if person i is Female0if person i is Male

Comparing Groups with Regression

  • In a regression, we can easily compare across groups via a dummy variable1

  • Dummy variable only =0 or =1, depending on if a condition is met

  • Signifies whether an observation belongs to a category or not

1 Also called a binary variable or dichotomous variable

Example:

^Wagei=^β0+^β1Femalei where Femalei={1if person i is Female0if person i is Male

  • Again, ^β1 makes less sense as the "slope" of a line in this context

Comparing Groups in Regression: Scatterplot

  • Female is our dummy x-variable

  • Hard to see relationships because of overplotting

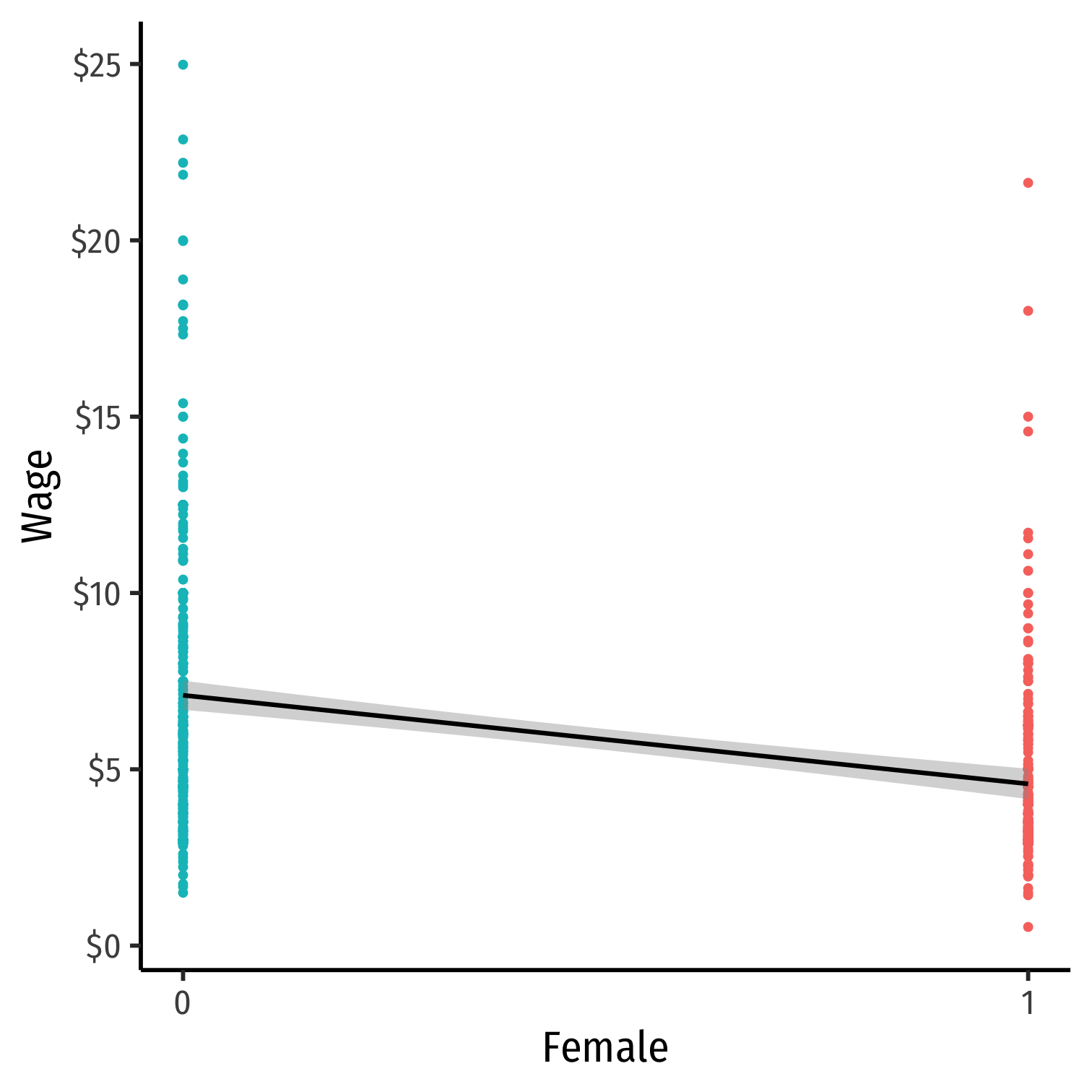
Comparing Groups in Regression: Scatterplot

  • Female is our dummy x-variable

  • Hard to see relationships because of overplotting

  • Use geom_jitter() instead of geom_point() to randomly nudge points

    • Only for plotting purposes, does not affect actual data, regression, etc.

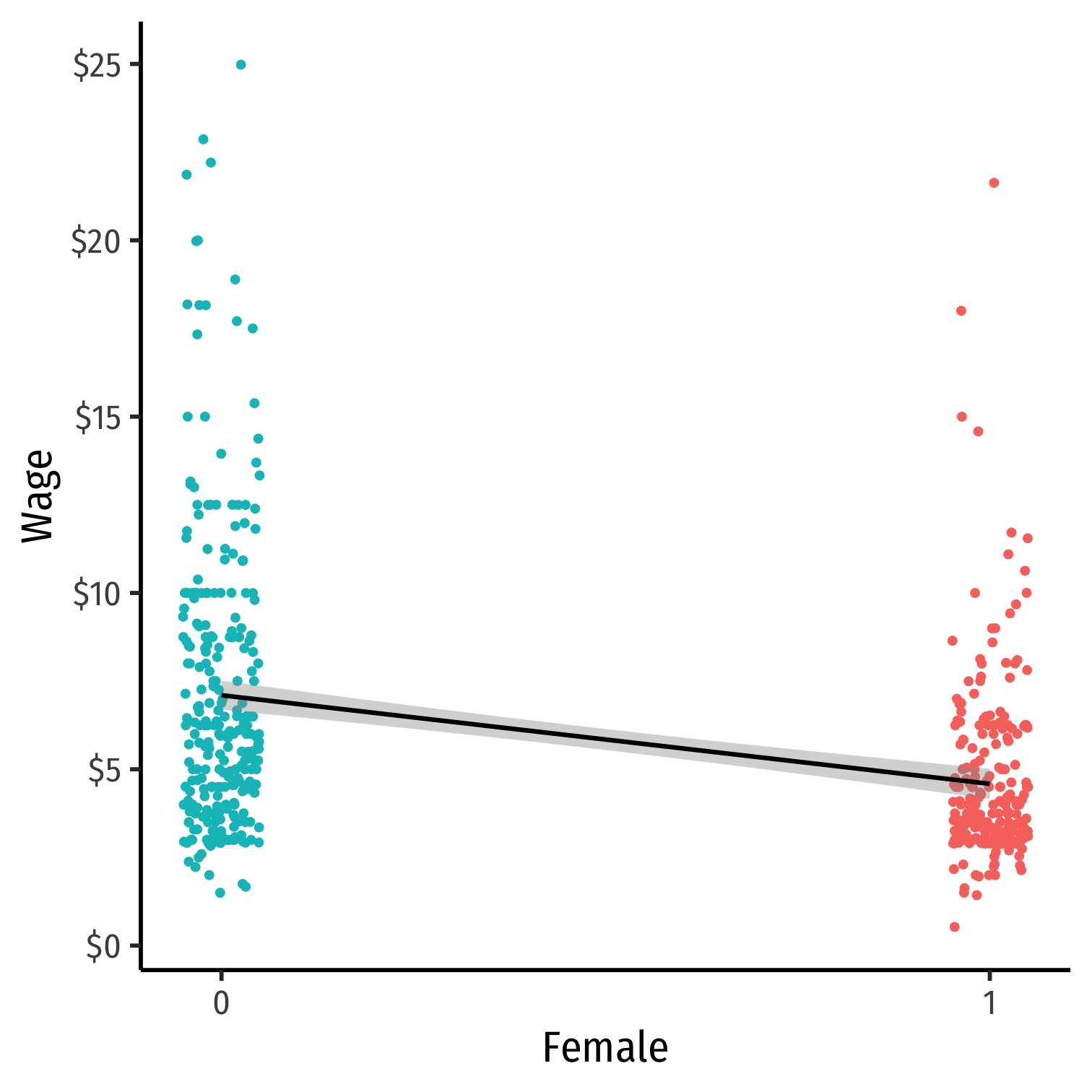
Comparing Groups in Regression: Scatterplot

  • Female is our dummy x-variable

  • Hard to see relationships because of overplotting

  • Use geom_jitter() instead of geom_point() to randomly nudge points

    • Only for plotting purposes, does not affect actual data, regression, etc.

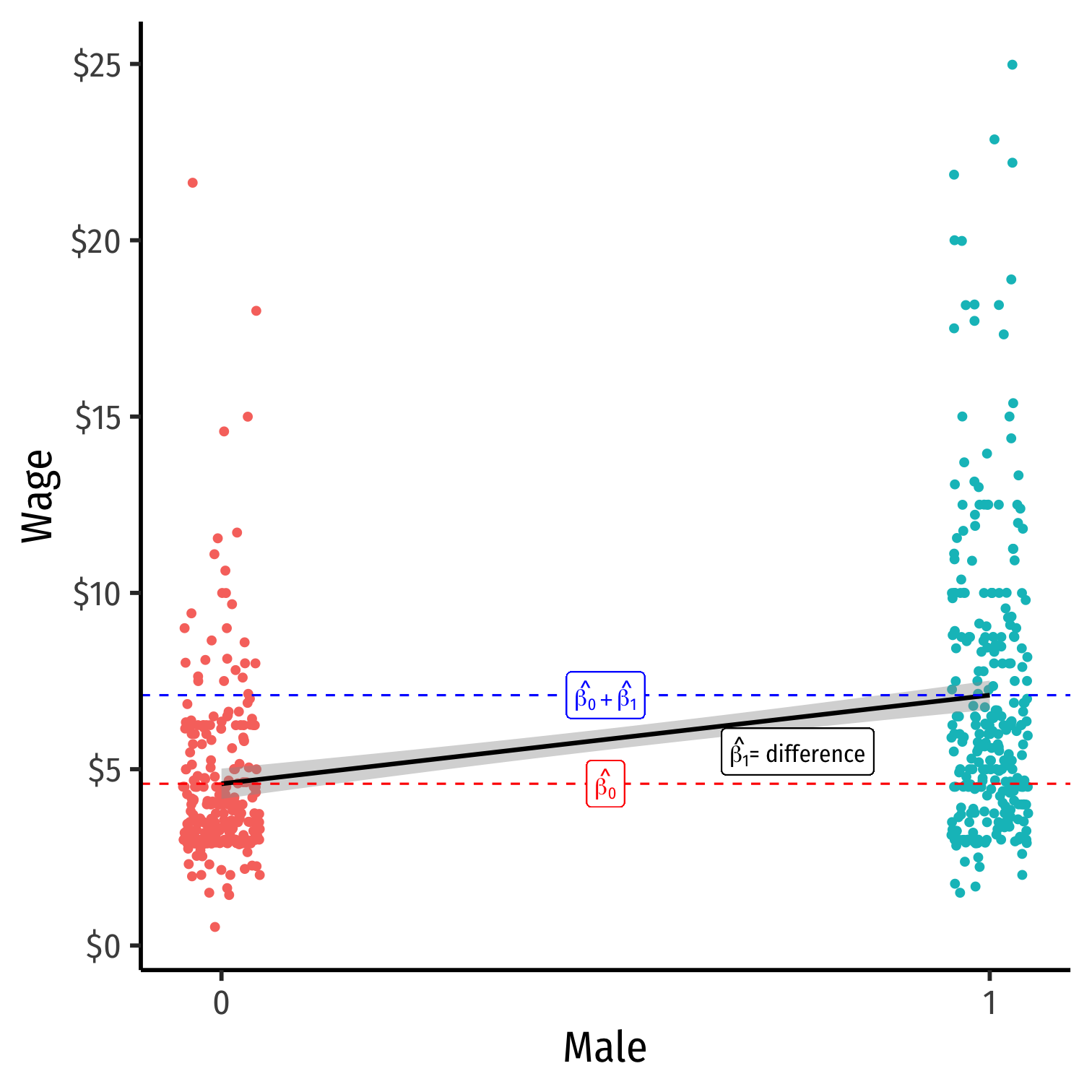
Dummy Variables as Group Means

^Yi=^β0+^β1Di where Di={0,1}

Dummy Variables as Group Means

^Yi=^β0+^β1Di where Di={0,1}

  • When Di=0 (Control group):
    • ^Yi=^β0
    • E[Y|Di=0]=^β0 ⟺ the mean of Y when Di=0

Dummy Variables as Group Means

^Yi=^β0+^β1Di where Di={0,1}

  • When Di=0 (Control group):

    • ^Yi=^β0
    • E[Y|Di=0]=^β0 ⟺ the mean of Y when Di=0

  • When Di=1 (Treatment group):

    • ^Yi=^β0+^β1Di
    • E[Y|Di=1]=^β0+^β1 ⟺ the mean of Y when Di=1

Dummy Variables as Group Means

^Yi=^β0+^β1Di where Di={0,1}

  • When Di=0 (Control group):

    • ^Yi=^β0
    • E[Y|Di=0]=^β0 ⟺ the mean of Y when Di=0

  • When Di=1 (Treatment group):

    • ^Yi=^β0+^β1Di
    • E[Y|Di=1]=^β0+^β1 ⟺ the mean of Y when Di=1
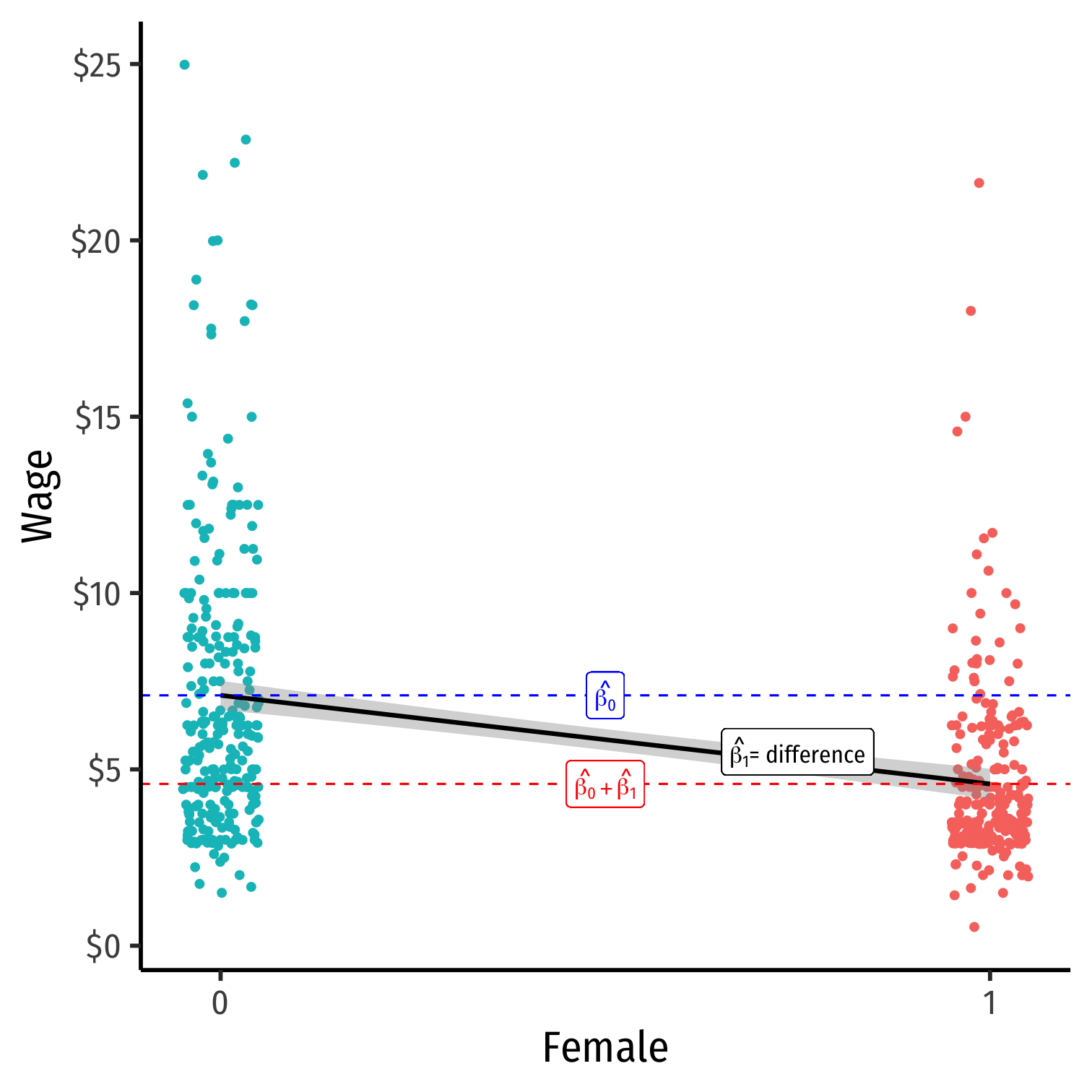
  • So the difference in group means:

=E[Yi|Di=1]−E[Yi|Di=0]=(^β0+^β1)−(^β0)=^β1

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men:

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

  • Mean wage for women:

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

  • Mean wage for women: E[Wage|Female=1]=^β0+^β1

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

  • Mean wage for women: E[Wage|Female=1]=^β0+^β1

  • Difference in wage between men & women:

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

  • Mean wage for women: E[Wage|Female=1]=^β0+^β1

  • Difference in wage between men & women: d=^β1

Comparing Groups in Regression: Scatterplot

  • Female is our dummy x-variable

  • Hard to see relationships because of overplotting

  • Use geom_jitter() instead of geom_point() to randomly nudge points

    • Only for plotting purposes, does not affect actual data, regression, etc.

The Data

# from wooldridge package
library(wooldridge)
# save as a dataframe
wages<-wooldridge::wage1
head(wages)
ABCDEFGHIJ0123456789
 
 
wage
<dbl>
educ
<int>
exper
<int>
tenure
<int>
nonwhite
<int>
female
<int>
married
<int>
numdep
<int>
smsa
<int>
13.10112001021
23.241222201131
33.00112000020
46.008442800101
55.30127200110
68.75169800101
6 rows | 1-10 of 25 columns

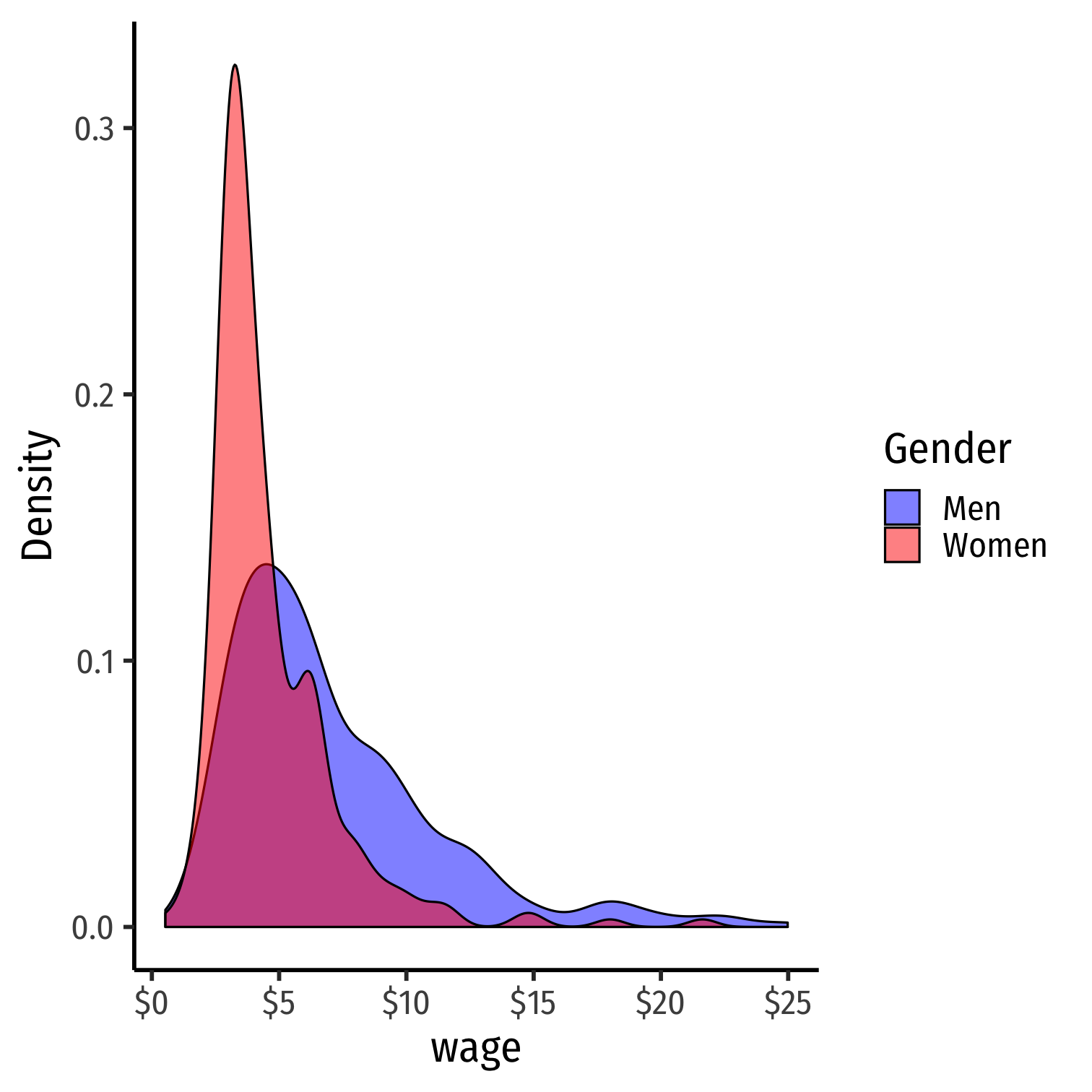
Get Group Averages & Std. Devs.

# Summarize for Men
wages %>%
  filter(female==0) %>%
  summarize(mean = mean(wage),
            sd = sd(wage))
ABCDEFGHIJ0123456789
mean
<dbl>
sd
<dbl>
7.0994894.160858
1 row
# Summarize for Women
wages %>%
  filter(female==1) %>%
  summarize(mean = mean(wage),
            sd = sd(wage))
ABCDEFGHIJ0123456789
mean
<dbl>
sd
<dbl>
4.5876592.529363
1 row

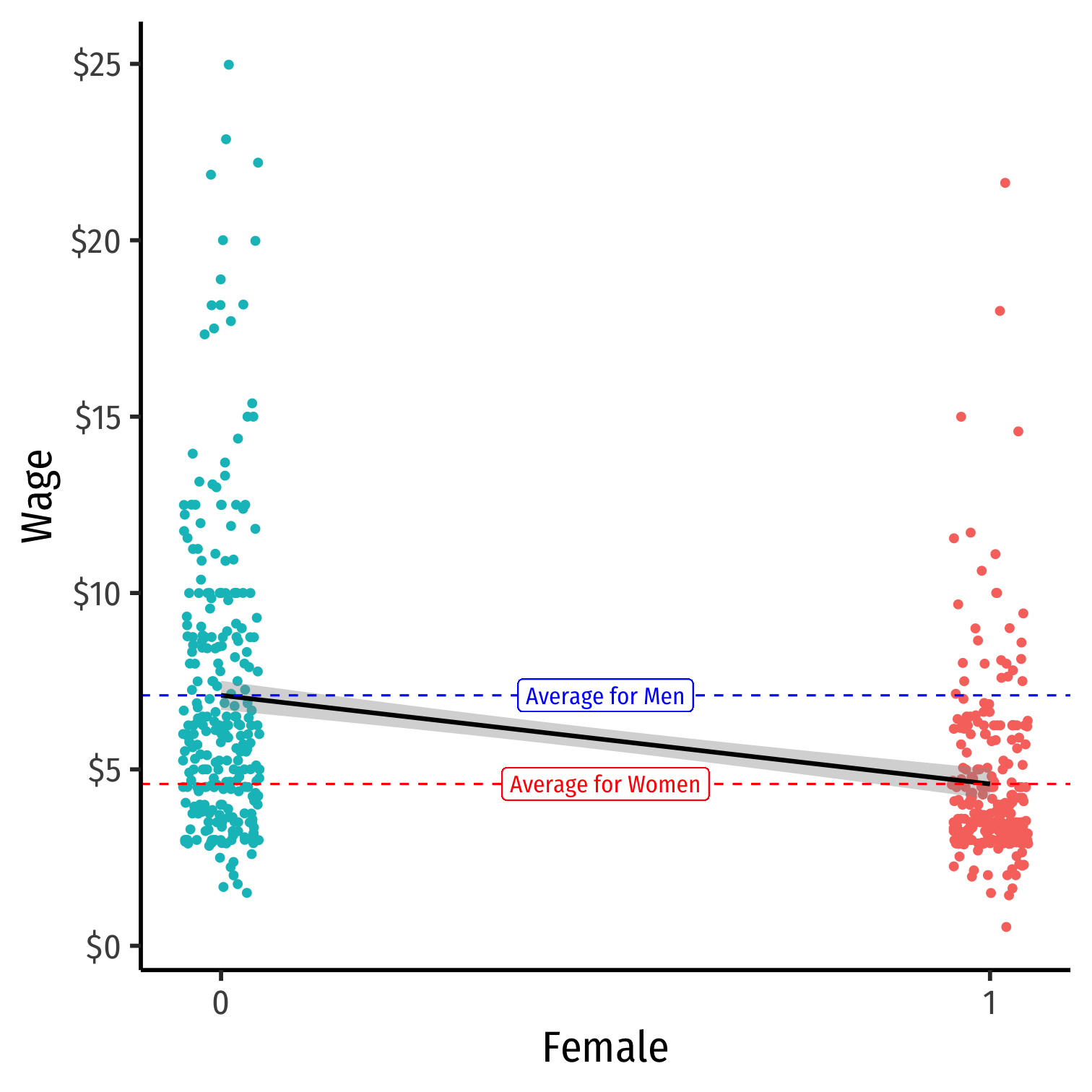
Visualize Differences

The Regression I

femalereg<-lm(wage~female, data=wages)
summary(femalereg)
## 
## Call:
## lm(formula = wage ~ female, data = wages)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.5995 -1.8495 -0.9877  1.4260 17.8805 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   7.0995     0.2100  33.806  < 2e-16 ***
## female       -2.5118     0.3034  -8.279 1.04e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.476 on 524 degrees of freedom
## Multiple R-squared:  0.1157,    Adjusted R-squared:  0.114 
## F-statistic: 68.54 on 1 and 524 DF,  p-value: 1.042e-15

The Regression II

library(broom)
tidy(femalereg)
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
p.value
<dbl>
(Intercept)7.0994890.210008233.8057778.971839e-134
female-2.5118300.3034092-8.2786881.041764e-15
2 rows

Dummy Regression vs. Group Means

From tabulation of group means

Gender Avg. Wage Std. Dev. n
Female 4.59 2.33 252
Male 7.10 4.16 274
Difference 2.51 0.30 −

From t-test of difference in group means

ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
(Intercept)7.0994890.2100082
female-2.5118300.3034092
2 rows | 1-3 of 5 columns

Recoding Dummies

Recoding Dummies

Example:

  • Suppose instead of female we had used:

^Wagei=^β0+^β1Malei where Malei={1if person i is Male0if person i is Female

Recoding Dummies with Data

ABCDEFGHIJ0123456789
 
 
wage
<dbl>
female
<int>
male
<dbl>
13.1010
23.2410
33.0001
46.0001
55.3001
68.7501
6 rows

Scatterplot with Male

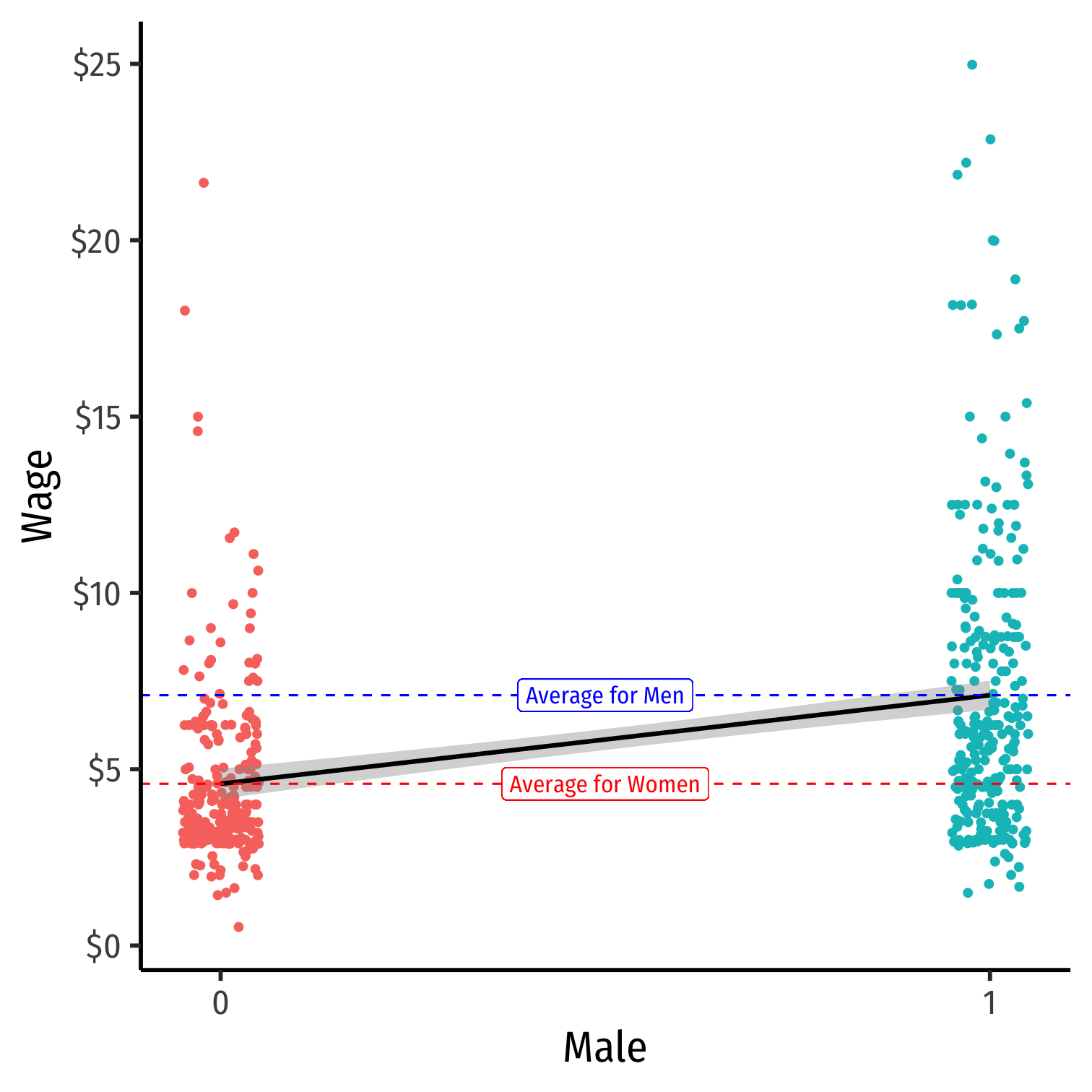
Dummy Variables as Group Means: With Male

Example:

^Wagei=^β0+^β1Malei

where Malei={1if i is Male0if i is Female

  • Mean wage for men: E[Wage|Male=1]=^β0+^β1

  • Mean wage for women: E[Wage|Male=0]=^β0

  • Difference in wage between men & women: d=^β1

Scatterplot with Male

The Regression with Male I

malereg<-lm(wage~male, data=wages)
summary(malereg)
## 
## Call:
## lm(formula = wage ~ male, data = wages)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.5995 -1.8495 -0.9877  1.4260 17.8805 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   4.5877     0.2190  20.950  < 2e-16 ***
## male          2.5118     0.3034   8.279 1.04e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.476 on 524 degrees of freedom
## Multiple R-squared:  0.1157,    Adjusted R-squared:  0.114 
## F-statistic: 68.54 on 1 and 524 DF,  p-value: 1.042e-15

The Regression with Male II

library(broom)
tidy(malereg)
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
p.value
<dbl>
(Intercept)4.5876590.218983420.9498023.012371e-71
male2.5118300.30340928.2786881.041764e-15
2 rows

The Dummy Regression: Male or Female

(1) (2)
Constant 4.59 *** 7.10 ***
(0.22)    (0.21)   
Female         -2.51 ***
        (0.30)   
Male 2.51 ***        
(0.30)           
N 526        526       
R-Squared 0.12     0.12    
SER 3.48     3.48    
*** p < 0.001; ** p < 0.01; * p < 0.05.

  • Note it doesn't matter if we use male or female, males always earn $2.51 more than females

  • Compare the constant (average for the D=0 group)

  • Should you use male AND female? We'll come to that...

Categorical Variables (More than 2 Categories)

Categorical Variables with More than 2 Categories

  • A categorical variable expresses membership in a category, where there is no ranking or hierarchy of the categories
    • We've looked at categorical variables with 2 categories only
    • e.g. Male/Female, Spring/Summer/Fall/Winter, Democratic/Republican/Independent

Categorical Variables with More than 2 Categories

  • A categorical variable expresses membership in a category, where there is no ranking or hierarchy of the categories
    • We've looked at categorical variables with 2 categories only
    • e.g. Male/Female, Spring/Summer/Fall/Winter, Democratic/Republican/Independent
  • Might be an ordinal variable expresses rank or an ordering of data, but not necessarily their relative magnitude
    • e.g. Order of finalists in a competition (1st, 2nd, 3rd)
    • e.g. Highest education attained (1=elementary school, 2=high school, 3=bachelor's degree, 4=graduate degree)

Using Categorical Variables in Regression I

Example: How do wages vary by region of the country? Let Regioni={Northeast,Midwest,South,West}

Using Categorical Variables in Regression I

Example: How do wages vary by region of the country? Let Regioni={Northeast,Midwest,South,West}

  • Can we run the following regression?

^Wagesi=^β0+^β1Regioni

Using Categorical Variables in Regression II

Example: How do wages vary by region of the country?

Code region numerically: Regioni={1if i is in Northeast2if i is in Midwest3if i is in South4if i is in West

Using Categorical Variables in Regression II

Example: How do wages vary by region of the country?

Code region numerically: Regioni={1if i is in Northeast2if i is in Midwest3if i is in South4if i is in West

  • Can we run the following regression?

^Wagesi=^β0+^β1Regioni

Using Categorical Variables in Regression III

Example: How do wages vary by region of the country?

Create a dummy variable for each region:

  • Northeasti=1 if i is in Northeast, otherwise =0
  • Midwesti=1 if i is in Midwest, otherwise =0
  • Southi=1 if i is in South, otherwise =0
  • Westi=1 if i is in West, otherwise =0

Using Categorical Variables in Regression III

Example: How do wages vary by region of the country?

Create a dummy variable for each region:

  • Northeasti=1 if i is in Northeast, otherwise =0
  • Midwesti=1 if i is in Midwest, otherwise =0
  • Southi=1 if i is in South, otherwise =0
  • Westi=1 if i is in West, otherwise =0
  • Can we run the following regression?

^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi+^β4Westi

Using Categorical Variables in Regression III

Example: How do wages vary by region of the country?

Create a dummy variable for each region:

  • Northeasti=1 if i is in Northeast, otherwise =0
  • Midwesti=1 if i is in Midwest, otherwise =0
  • Southi=1 if i is in South, otherwise =0
  • Westi=1 if i is in West, otherwise =0
  • Can we run the following regression?

^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi+^β4Westi

  • For every i:Northeasti+Midwesti+Southi+Westi=1!

The Dummy Variable Trap

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi+^β4Westi

  • If we include all possible categories, they are perfectly multicollinear, an exact linear function of one another:

Northeasti+Midwesti+Southi+Westi=1∀i

  • This is known as the dummy variable trap, a common source of perfect multicollinearity

The Reference Category

  • To avoid the dummy variable trap, always omit one category from the regression, known as the reference category

  • It does not matter which category we omit!

  • Coefficients on each dummy variable measure the difference between the reference category and each category dummy

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0:

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1:

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

  • ^β2:

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

  • ^β2: difference between West and Midwest

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

  • ^β2: difference between West and Midwest

  • ^β3:

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

  • ^β2: difference between West and Midwest

  • ^β3: difference between West and South

Dummy Variable Trap in R

summary(lm(wage~noreast+northcen+south+west, data=wages))
## 
## Call:
## lm(formula = wage ~ noreast + northcen + south + west, data = wages)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -6.083 -2.387 -1.097  1.157 18.610 
## 
## Coefficients: (1 not defined because of singularities)
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   6.6134     0.3891  16.995  < 2e-16 ***
## noreast      -0.2436     0.5154  -0.473  0.63664    
## northcen     -0.9029     0.5035  -1.793  0.07352 .  
## south        -1.2265     0.4728  -2.594  0.00974 ** 
## west              NA         NA      NA       NA    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.671 on 522 degrees of freedom
## Multiple R-squared:  0.0175,    Adjusted R-squared:  0.01185 
## F-statistic: 3.099 on 3 and 522 DF,  p-value: 0.02646

Using Different Reference Categories in R

# let's run 4 regressions, each one we omit a different region
no_noreast_reg<-lm(wage~northcen+south+west, data = wages)
no_northcen_reg<-lm(wage~noreast+south+west, data = wages)
no_south_reg<-lm(wage~noreast+northcen+west, data = wages)
no_west_reg<-lm(wage~noreast+northcen+south, data = wages)
# now make an output table
library(huxtable)
huxreg(no_noreast_reg,
       no_northcen_reg,
       no_south_reg,
       no_west_reg,
       coefs = c("Constant" = "(Intercept)",
                 "Northeast" = "noreast",
                 "Midwest" = "northcen",
                 "South" = "south",
                 "West" = "west"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 3)

Using Different Reference Categories in R II

(1) (2) (3) (4)
Constant 6.370 *** 5.710 *** 5.387 *** 6.613 ***
(0.338)    (0.320)    (0.268)    (0.389)   
Northeast          0.659     0.983 *   -0.244    
         (0.465)    (0.432)    (0.515)   
Midwest -0.659              0.324     -0.903    
(0.465)             (0.417)    (0.504)   
South -0.983 *   -0.324              -1.226 ** 
(0.432)    (0.417)             (0.473)   
West 0.244     0.903     1.226 **          
(0.515)    (0.504)    (0.473)            
N 526         526         526         526        
R-Squared 0.017     0.017     0.017     0.017    
SER 3.671     3.671     3.671     3.671    
*** p < 0.001; ** p < 0.01; * p < 0.05.

  • Constant is alsways average wage for reference (omitted) region

  • Compare coefficients between Midwest in (1) and Northeast in (2)...

  • Compare coefficients between West in (3) and South in (4)...

  • Does not matter which region we omit!

    • Same R2, SER, coefficients give same results

Dummy Dependent (Y) Variables

  • In many contexts, we will want to have our dependent ($Y$) variable be a dummy variable

Dummy Dependent (Y) Variables

  • In many contexts, we will want to have our dependent ($Y$) variable be a dummy variable

Example: ^Admittedi=^β0+^β1GPAi where Admittedi={1if i is Admitted0if i is Not Admitted

Dummy Dependent (Y) Variables

  • In many contexts, we will want to have our dependent ($Y$) variable be a dummy variable

Example: ^Admittedi=^β0+^β1GPAi where Admittedi={1if i is Admitted0if i is Not Admitted

  • A model where Y is a dummy is called a linear probability model, as it measures the probability of Y occuring (=1) given the X's, i.e. P(Yi=1|X1,⋯,Xk)
    • e.g. the probability person i is Admitted to a program with a given GPA

Dummy Dependent (Y) Variables

  • In many contexts, we will want to have our dependent ($Y$) variable be a dummy variable

Example: ^Admittedi=^β0+^β1GPAi where Admittedi={1if i is Admitted0if i is Not Admitted

  • A model where Y is a dummy is called a linear probability model, as it measures the probability of Y occuring (=1) given the X's, i.e. P(Yi=1|X1,⋯,Xk)
    • e.g. the probability person i is Admitted to a program with a given GPA

  • Requires special tools to properly interpret and extend this (logit, probit, etc)

  • Feel free to write papers that have dummy Y variables (but you may have to ask me some more questions)!

Categorical Data

  • Categorical data place an individual into one of several possible categories

    • e.g. sex, season, political party
    • may be responses to survey questions
    • can be quantitative (e.g. age, zip code)

  • R calls these factors (we'll deal with them much later in the course)

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow