+ - 0:00:00
Notes for current slide
Notes for next slide

3.5: Causal Inference and DAGs

ECON 480 · Econometrics · Fall 2019

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsf19
metricsF19.classes.ryansafner.com

Causality

  • Statistics profession is obstinant that we cannot say anything about causality

    • Statisticians: causation is simply a subset of correlation, where correlation is −1 or 1

  • But you have to! It's how the human brain works!

  • We can't concieve of (spurious) correlation without some causation

RCTs are All the Rage

Source: Vox (Oct 14, 2019)

But Not Everyone Agrees I

Angus Deaton

Economics Nobel 2015

The RCT is a useful tool, but I think that is a mistake to put method ahead of substance. I have written papers using RCTs. Like other methods of investigation, they are often useful, and, like other methods, they have dangers and drawbacks. Methodological prejudice can only tie our hands...It is not true that an RCT, when feasible, will always do better than an observational study. This should not be controversial [but] might still make some uncomfortable, particularly the second [statement]: (a) RCTs are affected by the same problems of inference and estimation that economists have faced using other methods, and (b) no RCT can ever legitimately claim to have established causality. My theme is that RCTs have no special status, they have no exemption from the problems of inference that econometricians have always wrestled with, and there is nothing that they, and only they, can accomplish.

Deaton, Angus, 2019, "Randomization in the Tropics Revisited: A Theme and Eleven Variations," Working Paper

But Not Everyone Agrees II

Lant Pritchett

People keep saying that the recent Nobelists "studied global poverty." This is exactly wrong. They made a commitment to a method, not a subject, and their commitment to method prevented them from studying global poverty.

At a conference at Brookings in 2008 Paul Romer (last years Nobelist) said: "You guys are like going to a doctor who says you have an allergy and you have cancer. With the skin rash we can divide you skin into areas and test variety of substances and identify with precision and some certainty the cause. Cancer we have some ideas how to treat it but there are a variety of approaches and since we cannot be sure and precise about which is best for you, we will ignore the cancer and not treat it."

Source

But Not Everyone Agrees III

Angus Deaton

Economics Nobel 2015

"Lant Pritchett is so fun to listen to, sometimes you could forget that he is completely full of shit."

Source

RCTs and Evidence-Based Policy I

  • Programs randomly assign treatment to different individuals and measure causal effect of treatment

  • RAND Health Insurance Study

  • Oregon Medicaid Expansion

  • HUD's Moving to Opportunity

  • Tennessee STAR

RCTs and Evidence-Based Policy II

  • Should we ONLY base policies on the evidence from Randomized Controlled Trials?

RCTs and Evidence-Based Policy II

  • Should we ONLY base policies on the evidence from Randomized Controlled Trials?

RCTs and Evidence-Based Policy II

  • Should we ONLY base policies on the evidence from Randomized Controlled Trials?

Source: British Medical Journal

RCTs and Evidence-Based Policy III

RCTs and Evidence-Based Policy III

Correlation and Causation I

Correlation and Causation II

Correlation and Causation

  • Correlation:

    • Math & Statistics
    • Computers, AI, Machine learning can figure this out (even better than humans)

  • Causation:

    • Philosophy, Intuition, Theory
    • Counterfactual thinking, unique to humans (vs. animals or machines)
    • Computers cannot yet figure this out

Causation Requires Counterfactual Thinking

Recall: The Fundamental Problem of Causal Inference I

John Maria
Y0J=3 Y0M=5
Y1J=4 Y1M=5
Y1J−Y0J=1 Y1M−Y0M=0
YJ=(Y1J)=4 YM=(Y0M)=5

  • Recall example from class 1.2

  • John will choose to buy health insurance

  • Maria will choose to not buy health insurance

  • Health insurance improves John's score by 1, has no effect on Maria's score

  • Note, all we can observe in the data are their health outcomes after they have chosen (not) to buy health insurance: YJ=4 and YM=5

  • Observed difference between John and Maria: YJ−YM=−1

Recall: Counterfactuals

John Maria
YJ=4 YM=5

This is all the data we actually observe

  • Observed difference between John and Maria: YJ−YM=Y1J−Y0M⏟=−1

  • Recall:

    • John has bought health insurance (Y1J)
    • Maria has not bought insurance (Y0M)

  • We don't see the counterfactuals:

    • John's score without insurance
    • Maria score with insurance

Causal Inference

  • We will seek to understand what causality is and how we can approach finding it

  • We will also explore the different common research designs meant to identify causal relationships

  • These skills, more than supply & demand, constrained optimization models, ISLM, etc, are the tools and comparative advantage of a modern research economist

    • Why all big companies (especially in tech) have entire economics departments in them

Clever Research Designs Identify Causality

What Then IS Causation?

  • X causes Y if we can intervene and change X without changing anything else, and Y changes
  • Y "listens to" X
    • X may not be the only thing that causes Y

What Then IS Causation?

  • X causes Y if we can intervene and change X without changing anything else, and Y changes
  • Y "listens to" X
    • X may not be the only thing that causes Y

Example

If X is a light switch, and Y is a light:

  • Flipping the switch (X) causes the light to go on (Y)
  • But NOT if the light is burnt out (No Y despite X)
  • OR if the light was already on (Y without X)

Less-Clear Causal Claims

Example

  • Getting a college degree raises your wages

Less-Clear Causal Claims

Example

  • Getting a college degree raises your wages

Example

  • Tariffs reduce the volume of international trade

Non-Causal Claims

  • All of the following have non-zero correlations. Are they causal?

Example

  • Greater ice cream sales cause more violent crime
  • Rooster crows cause the sun to rise in the morning

Non-Causal Claims

  • All of the following have non-zero correlations. Are they causal?

Example

  • Greater ice cream sales cause more violent crime
  • Rooster crows cause the sun to rise in the morning
  • Less clear:

Example

  • Colds tend to clear up a few days after you take Vitamin-C
  • The economy performs better or worse depending on the political party in power

Counterfactuals

  • The sine qua non of causal claims are counterfactuals: what would Y have been if X had been different?
  • It is impossible to make a counterfactual claim from data alone! Need a causal model of the data-generating process!

Counterfactuals and RCTs

  • Again, RCTs are invoked as the gold standard for their ability to make counterfactual claims:
  • Treatment/intervention (X) is randomly assigned to individuals, and then outcome Y is measured

If person i who recieved treatment had not recieved the treatment, we can predict what his outcome would have been

If person j who did not recieve treatment had recieved treatment, we can predict what her outcome would have been

  • We can say this because, on average, treatment and control groups are the same before treatment

From RCTs to Causal Models

  • RCTs are but the best-known method of a large, growing science of causal inference
  • We need a causal model to describe the data-generating process (DGP)
  • Requires us to make some assumptions

Causal Diagrams

Causal Diagrams/DAGs

  • A surprisingly simple, yet rigorous and powerful method of modeling is using a causal diagram or Directed Acyclic Graph (DAG)

  • A simple series of nodes (variables) connected by arrows that indicate causal effects

    • Arrows can only go one way ("directed") and can never loop back ("acyclic")

Drawing a DAG

  • Causal diagram (DAG) is the model of what you think the data-generating process is

  • Useful to help figure out how to identify particular relationships of interest

  • Requires some common sense/economic intutition

  • Remember, all models are wrong, we just need them to be useful!

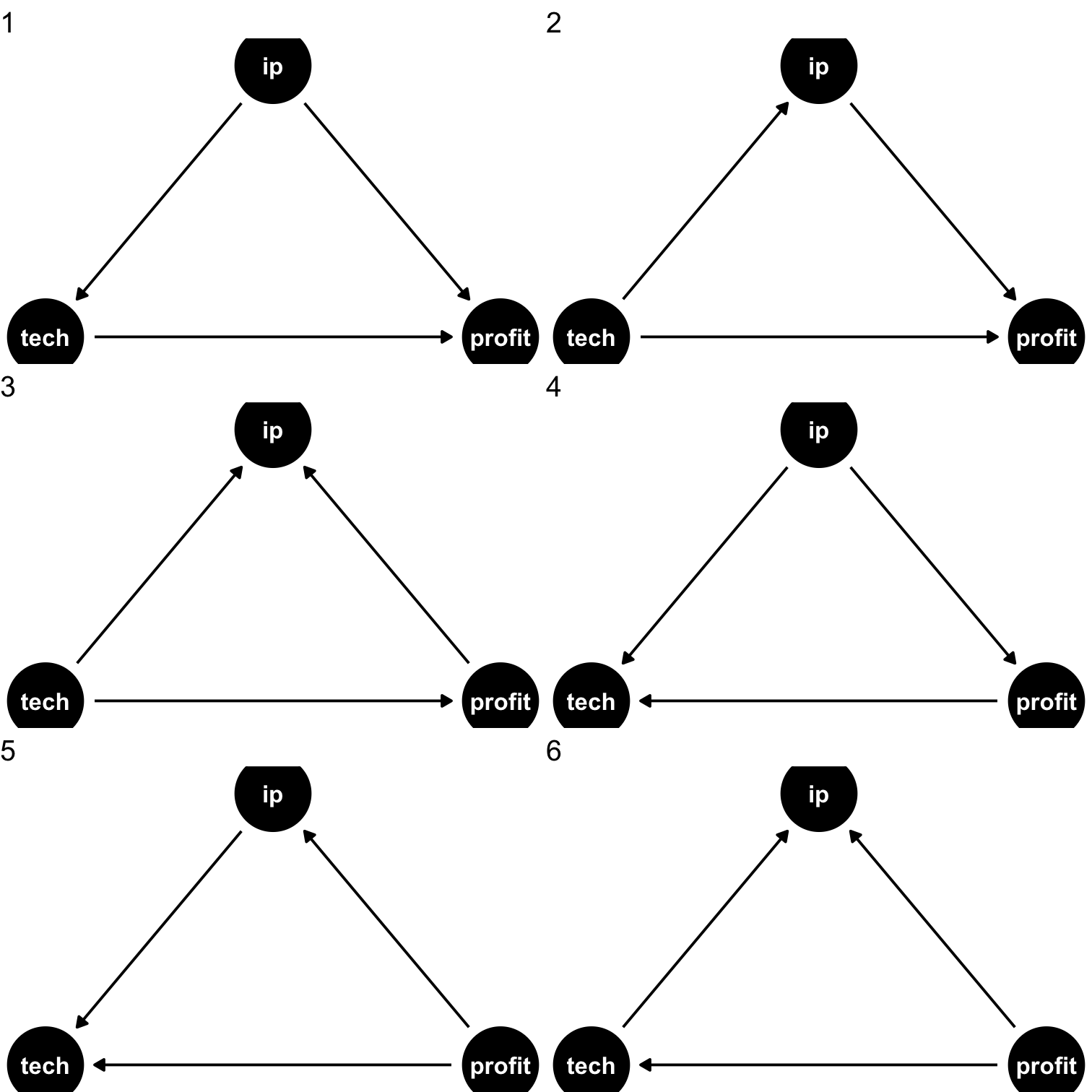
Drawing a DAG: Example

  • Suppose we have data on three variables

    • IP: how much a firm spends on IP lawsuits
    • tech: whether a firm is in tech industry
    • profit: firm profits

  • They are all correlated with each other, but what's are the causal relationships?

  • We need our own causal model (from theory, intuition, etc) to sort

    • Data alone will not tell us!

Drawing a DAG:

  1. Consider all the variables likely to be important to the data-generating process (including variables we can't observe!)

  2. For simplicity, combine some similar ones together or prune those that aren't very important

  3. Consider which variables are likely to affect others, and draw arrows connecting them

  4. Test some testable implications of the model (to see if we have a correct one!)

Side Notes

  • Drawing an arrow requires a direction - making a statement about causality!

  • Omitting an arrow makes an equally important statement too!

    • In fact, we will need omitted arrows to show causality!

  • If two variables are correlated, but neither causes the other, it's likely they are both caused by another (perhaps unobserved) variable - add it!

  • There should be no cycles or loops (if so, there's probably another missing variable, such as time)

DAG Example I

Example: what is the effect of education on wages?

  • Education ("treatment" or "exposure")

  • Wages ("outcome" or "response")

DAG Example I

  • What other variables are important?
    • Ability
    • Socioeconomic status
    • Demographics
    • Phys. Ed. requirements
    • Year of birth
    • Location
    • Schooling laws
    • Job connections

DAG Example I

  • In social science and complex systems, 1000s of variables could plausibly be in DAG!

  • So simplify:

    • Ignore trivial things (Phys. Ed. requirement)
    • Combine similar variables (Socioeconomic status, Demographics, Location → Background)

DAG Example II

  • Background, Year of birth, Location, Compulsory schooling, all cause education

  • Background, year of birth, location, job connections probably cause wages

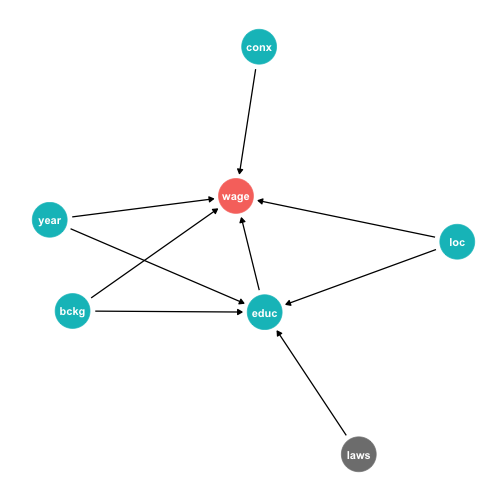
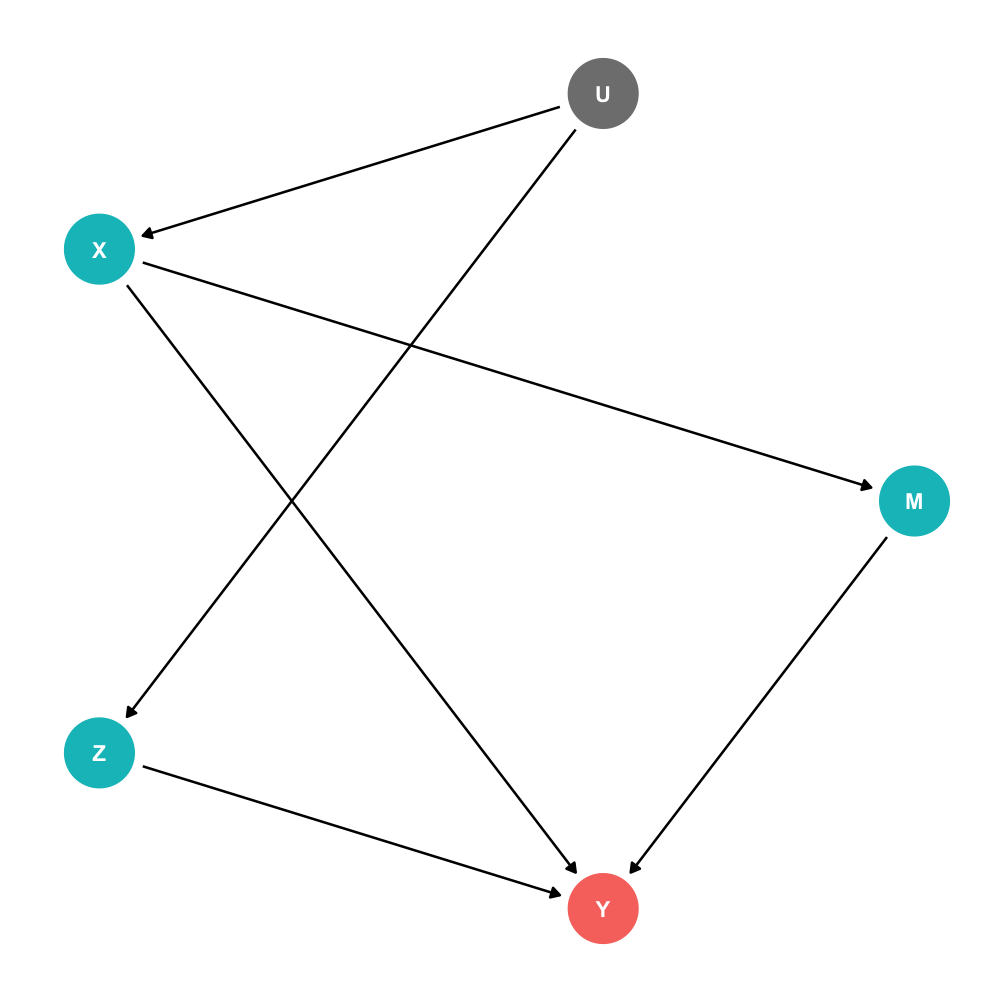
DAG Example III

  • Background, Year of birth, Location, Compulsory schooling, all cause education

  • Background, year of birth, location, job connections probably cause wages

  • Job connections in fact is probably caused by education!

  • Location and background probably both caused by unobserved factor (u1)

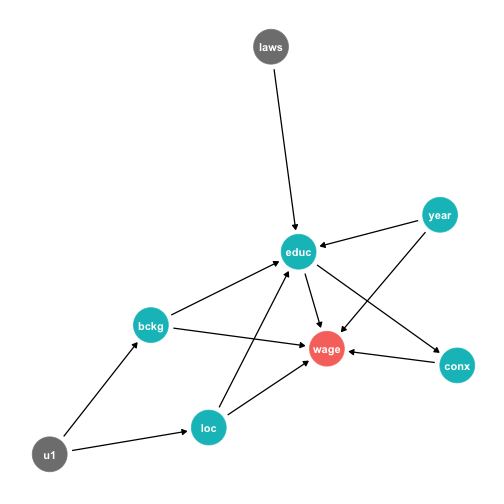
DAG Example IV

  • This is messy, but we have a causal model!

  • Makes our assumptions explicit, and many of them are testable

  • DAG suggests certain relationships that will not exist:

    • all relationships between laws and conx go through educ
    • so if we controlled for educ, then cor(laws,conx) should be zero!

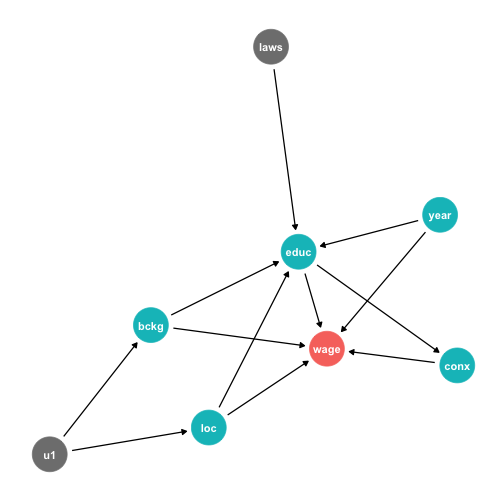
Let the Computer Do It: Dagitty.net I

  • Dagitty.net is a great tool to make these and give you testable implications

  • Click Model -> New Model

  • Name your "exposure" variable (X of interest) and "outcome" variable (Y)

Let the Computer Do It: Dagitty.net II

  • Click and drag to move nodes around

  • Add a new variable by double-clicking

  • Add an arrow by double-clicking one variable and then double-clicking on the target (do again to remove arrow)

Let the Computer Do It: Dagitty.net III

  • Tells you how to identify your effect! (upper right)

Minimal sufficient adjustment sets containing background, location, year for estimating the total effect of educ on wage: background, location, year

  • Tells you some testable implications (middle right)
    • conditional independencies, take the last one:
    • job_connections ⊥ year | educ
    • means: holding constant educ, there should be no correlation between job_connections and year - can test this with data!

Implications

  • In order to identify the effect of education on wages, our model implies we need to control for background, location, and year
    • note: we do not need to control for anything else!

Implications

  • In order to identify the effect of education on wages, our model implies we need to control for background, location, and year

    • note: we do not need to control for anything else!

  • How to control for them?

    • many ways, we've learned one: multivariate regression:

Implications

  • In order to identify the effect of education on wages, our model implies we need to control for background, location, and year

    • note: we do not need to control for anything else!

  • How to control for them?

    • many ways, we've learned one: multivariate regression:

wages=β0+β1educ+β2background+β3location+β4year

Implications

  • In order to identify the effect of education on wages, our model implies we need to control for background, location, and year

    • note: we do not need to control for anything else!

  • How to control for them?

    • many ways, we've learned one: multivariate regression:

wages=β0+β1educ+β2background+β3location+β4year

  • How did Dagitty know what we needed to do? Some simple rules (below)

Causal Effect

  • If we control for background, location, and year, we can identify the causal effect of educ → wage.

You Can Draw DAGs In R

  • New package: ggdag
  • Arrows are made with formula notation: Y~X means "Y is caused by X"
library(ggdag)
dagify(wage~educ+conx+year+bckg+loc,
       educ~bckg+year+loc+laws,
       conx~educ,
       bckg~u1,
       loc~u1) %>% 
  ggdag()+
  theme_dag()

DAG Rules

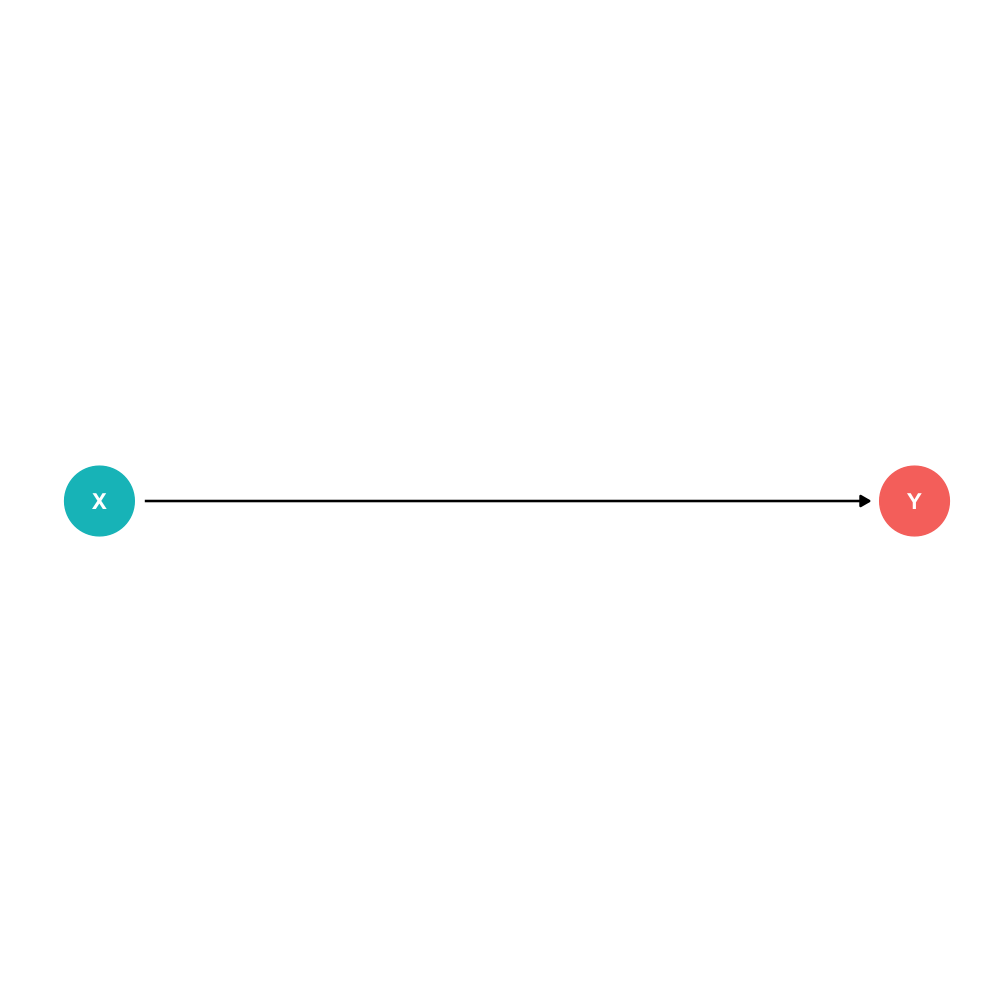
DAGs I

  • Typical notation:

  • X is independent variable of interest

    • Epidemiology: "intervention"

  • Y is dependent/"response" variable

  • Other variables use other letters

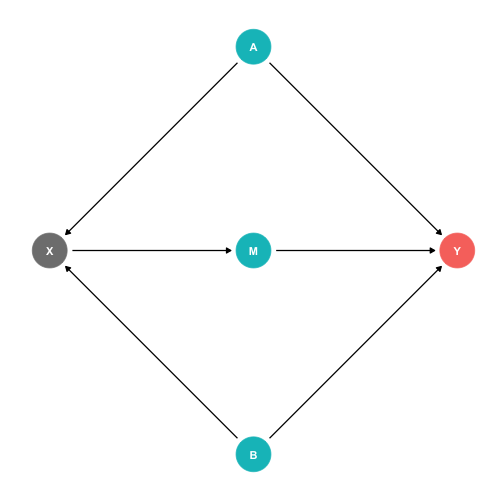
DAGs and Causal Effects

  • Arrows indicate causal effect (in proper direction)

  • Two types of causal effect:

    1. Direct effects X→Y

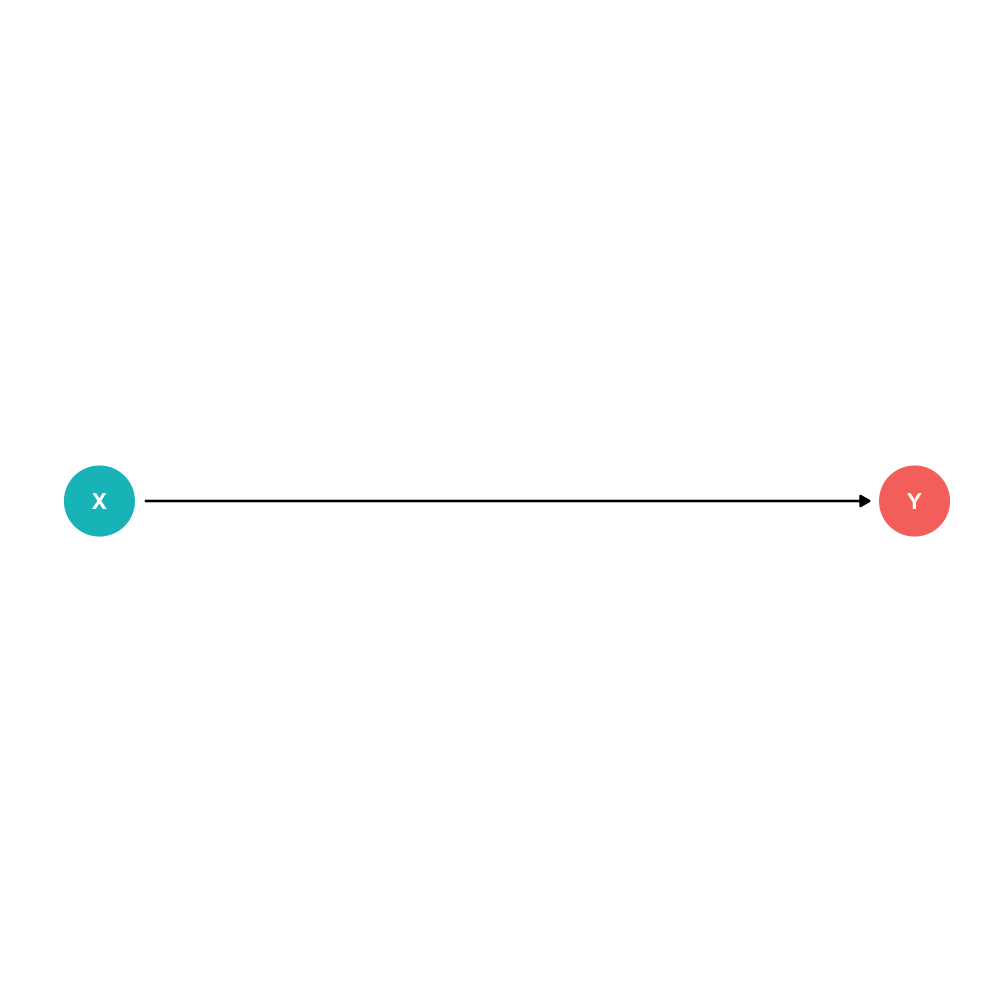
DAGs and Causal Effects

  • Arrows indicate causal effect (in proper direction)

  • Two types of causal effect:

  1. Direct effects X→Y

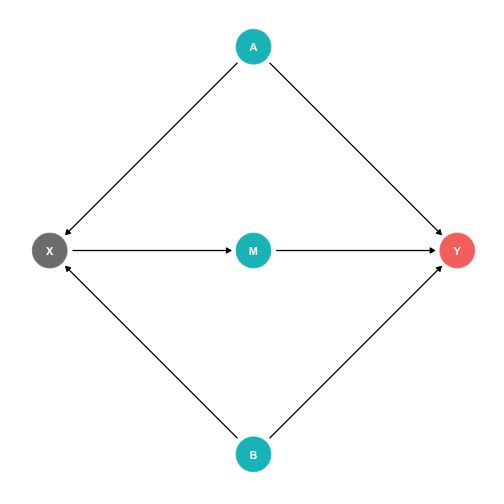
  2. Indirect effects X→M→Y

    • M is a "mediator" variable, the mechanism by which X affects Y

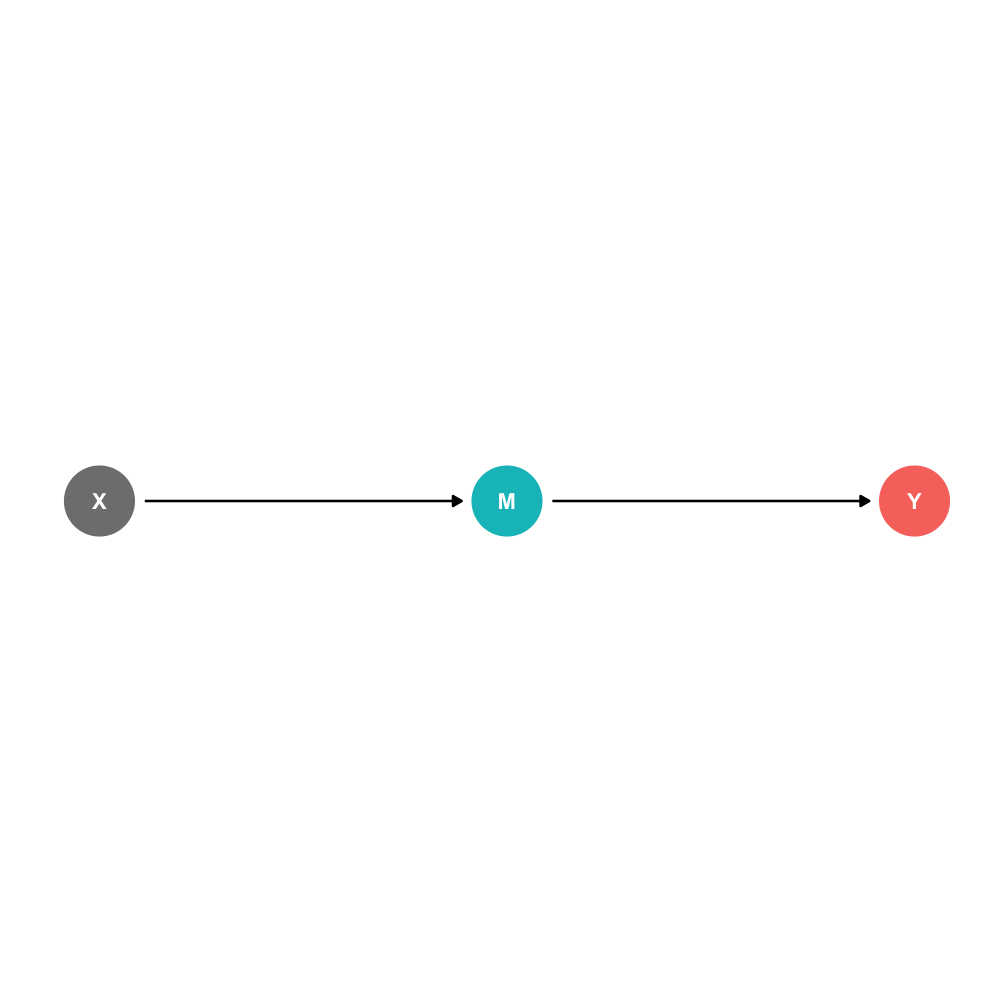
DAGs and Causal Effects

  • Arrows indicate causal effect (in proper direction)

  • Two types of causal effect:

  1. Direct effects X→Y

  2. Indirect effects X→M→Y

    • M is a "mediator" variable, the mechanism by which X affects Y

  3. You of course might have both!

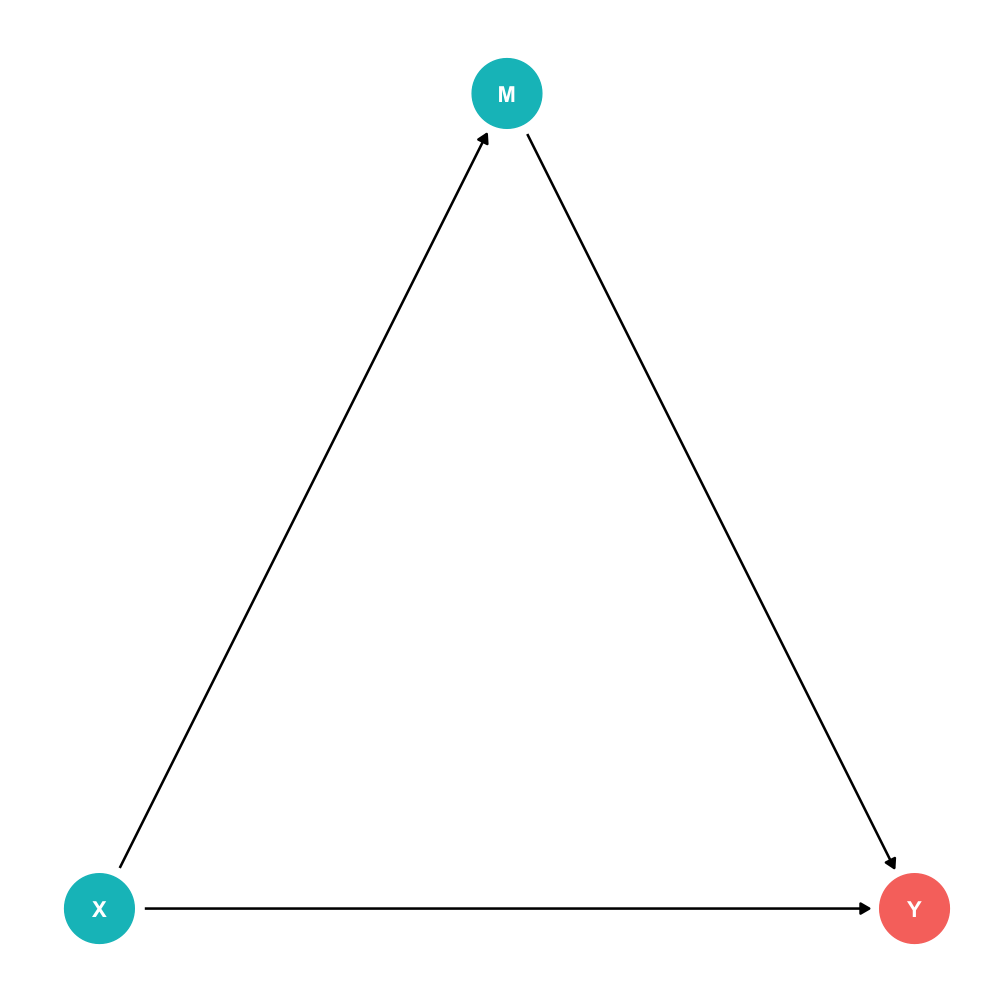
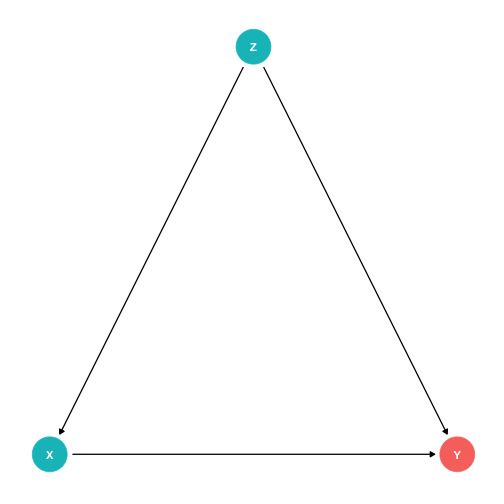
Confounders

  • Z is a confounder of X→Y, Z affects both X and Y

  • cor(X,Y) is made up of two parts:

    • The value of Y is affected by the value of X (X→Y, good!)
    • Z affects both the values of X and Y (A spurious correlation between X and Y, bad!)

  • Failing to control for Z will bias our estimate of the causal effect of X→Y!

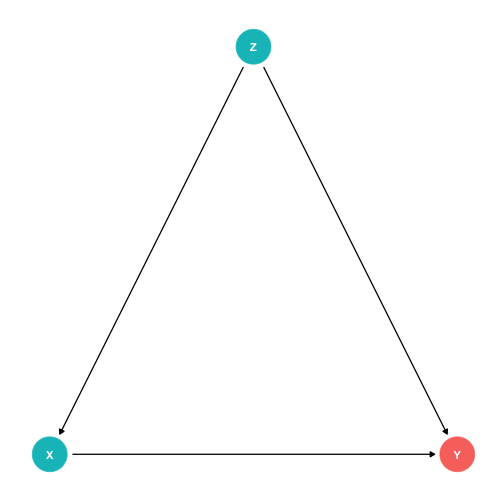
Confounders

  • Confounders are the DAG-equivalent of omitted variable bias

  • Biased regression Y=β0+β1X leaving out Z

  • ˆβ1 picks up both:

    • X→Y
    • X←Z→Y

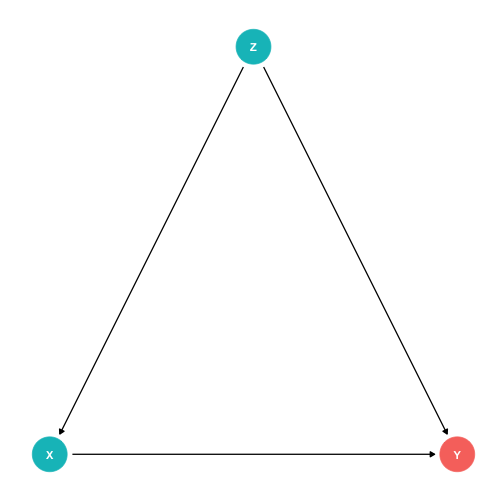
Front Doors and Back Doors

  • With this graph, there are two paths that connect X and Y1:

  1. A causal "front-door" path X→Y

    • Good, what we want to measure

  2. A non-causal "back-door" path X←Z→Y

    • At least one causal arrow runs in the opposite direction
    • Bad, adds a confounding bias

1 Regardless of the directions of the arrows!

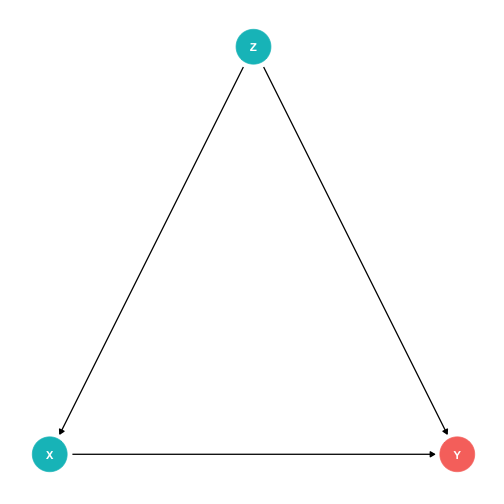
Controlling I

  • If we can control for Z, we can block the back-door path X←Z→Y

    • Essentially, delete the arrow(s) connecting X, Z, and Y

  • This would only leave the front-door, X→Y

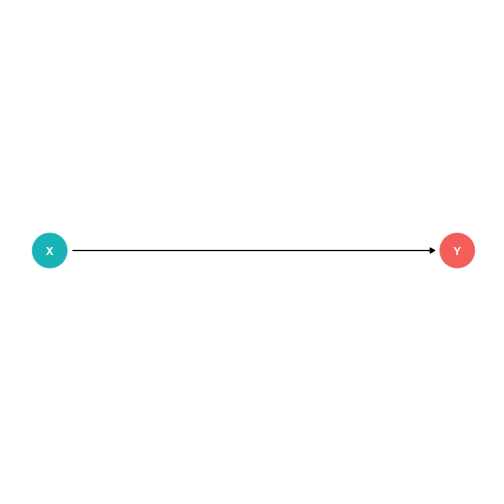
Controlling II

  • How to "control for" Z? We want to remove its influence over determining the values of X and Y

  • Multiple methods exist, but we've done this with multivariate regression

  • At the simplest level, consider only looking at values of X and Y for all observations that have the same value of Z

    • removes causal influence Z has on X and on Y
    • leaves only the influence X has on Y!

Controlling III

  • Controlling for a single variable along a long causal path is sufficient to block that path!

  • Causal path: X→Y

  • Backdoor path: X←A→B→C→Y

  • It is sufficient to block this backdoor by controlling either A or B or C!

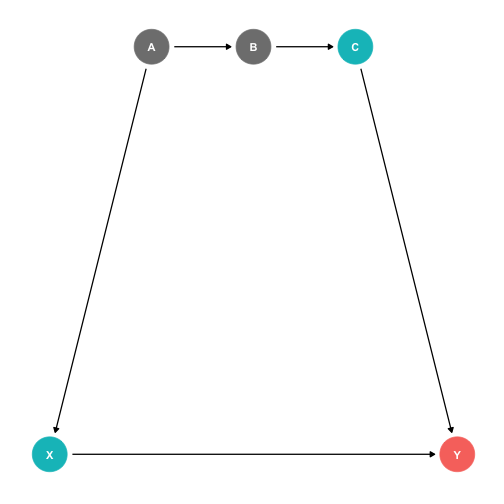
The Back Door Criterion

  • To achieve proper identification of the causal effect:

  • The "back-door criterion": control for the minimal amount of variables sufficient to ensure that no back-door exists between X and Y

The Back Door Criterion

  • Implications of the Back-door criterion:
  1. You only need to control for the variables that keep a back-door open, not all other variables!

Example:

  • X→Y (front-door)

  • X←A→B→Y (back-door)

  • Need only control for A or B to block the one back-door path

  • Z has no effect on X, and therefore we don't need to control for it!

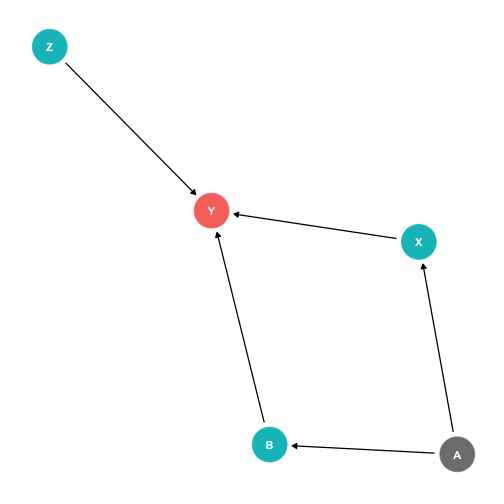
The Back Door Criterion: Colliders

  • A case where controlling for a variable actually adds bias is if that variable is known as a "collider".

Example:

  • X→Y (front-door)

  • X←A→B←C→Y (back-door, but blocked by collider!)

  • B is a collider because both A and C point to it

  • A collider automatically blocks a path
  • If you control for the collider, it opens a path (bad idea if it's a backdoor path)

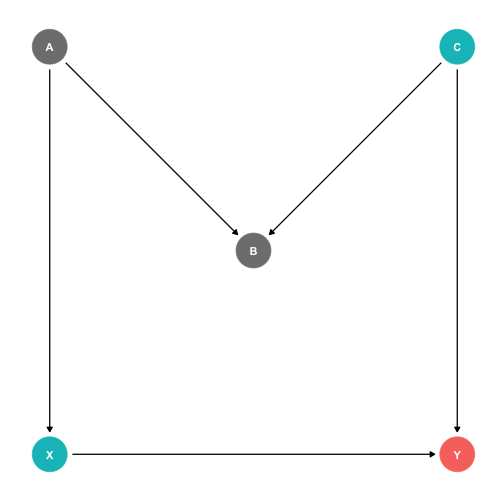
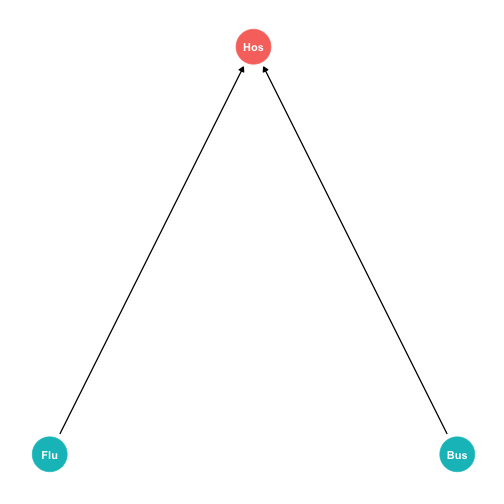
The Back Door Criterion: Colliders

Example:

  • Flu: getting the flu
  • Bus: being hit by a bus

  • Hos: being in the hospital

  • Both Flu and Bus send you to Hos (arrows)

  • Knowing Flu doesn't tell us about Bus (no arrow)

  • Conditional on being in Hos, negative association between Flu and Bus (spurious!)

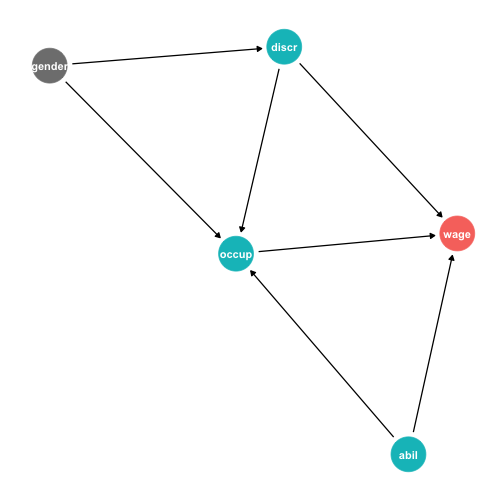
Collider Example: Gender Discrimination I

Example: How much of wage disparities are caused by gender-based discrimination?

  1. discr→wage (Causal path)
  2. discr→occup→wage (Causal path)
  3. discr←gender→occup→wage (BLOCKED back door!)
  4. discr←gender→occup←abil→wage (BLOCKED back door!)
  5. discr→occup←abil→wage (BLOCKED back door!)
  • Should we control for occup?

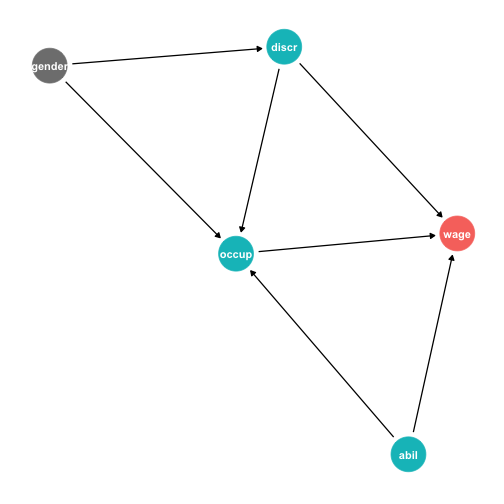
Collider Example: Gender Discrimination II

  • If we control for occupation:

    • opens backdoor paths 3, 4, 5!
    • creates spurious cor(abil,discr) where there wasn't one!
    • also closes causal path 2! (discriminatory reasons genders choose different occupations)

  • Can't identify causal effect controlling for occup alone!

    • Could if you could control for occup and abil (but perhaps abil is unobserved)

The Front Door Criterion: Mediators I

  • Another case where controlling for a variable actually adds bias is if that variable is known as a "mediator".

Example:

  • X→M→Y (front-door)
  • X←A→Y (back-door)

  • X←B→Y (back-door)

  • Should we control for M?

  • If we did, this would block the front-door!

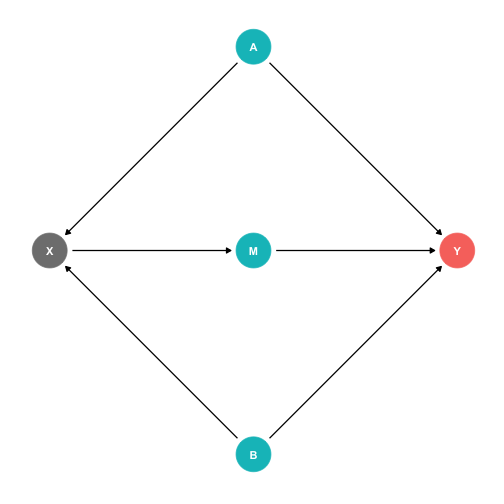
The Front Door Criterion: Mediators II

  • Another case where controlling for a variable actually adds bias is if that variable is known as a "mediator".

Example:

  • If we control for M, this would block the front-door!

  • If we can estimate X→M and M→Y (note, no back-doors to either of these!), we can estimate X→Y

  • This is the front door method

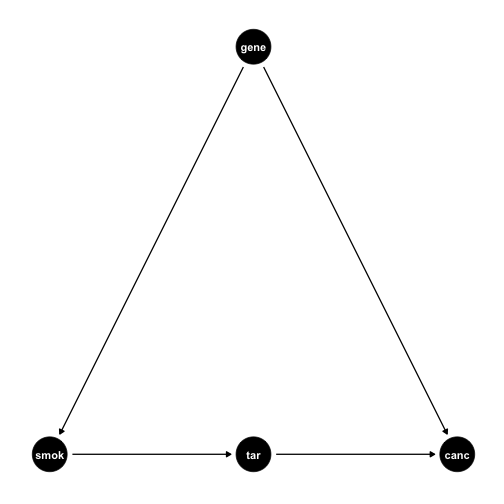
The Front Door Criterion: Mediators III

  • Tobacco industry claimed that cor(smoking,cancer) could be spurious due to a confounding gene that affects both!

    • Smoking gene is unobservable

  • Suppose smoking causes tar buildup in lungs, which cause cancer

  • We should not control for tar, it's on the front-door path

    • This is how scientific studies can relate smoking to cancer

Recap

Thus, to achieve causal identification, control for the minimal amount of variables such that:

  1. Ensure that no back-door path remains open

    • Close back-door paths by controlling for any variable along that path
    • Colliders along a path automatically close that path

  2. Ensure that no front-door path is closed

Causality

  • Statistics profession is obstinant that we cannot say anything about causality

    • Statisticians: causation is simply a subset of correlation, where correlation is −1 or 1

  • But you have to! It's how the human brain works!

  • We can't concieve of (spurious) correlation without some causation

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow