+ - 0:00:00
Notes for current slide
Notes for next slide

3.2: Multivariate OLS Estimators: Bias, Precision, and Fit

ECON 480 · Econometrics · Fall 2019

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsf19
metricsF19.classes.ryansafner.com

The Multivariate OLS Estimators

The Multivariate OLS Estimators

  • By analogy, we still focus on the ordinary least squares (OLS) estimators of the unknown population parameters β0,β1,β2,⋯,βk which solves:

min^β0,^β1,^β2,⋯,^βkn∑i=1[Yi−(^β0+^β1X1i+^β2X2i+⋯+^βkXki)⏟ui]2

  • Again, OLS estimators are chosen to minimize the sum of squared errors (SSE)
    • i.e. the sum of the squared distances between the actual values of Yi and the predicted values ^Yi

The Multivariate OLS Estimators: FYI

Math FYI: in linear algebra terms, a regression model with n observations of k independent variables:

Y=Xβ+u

(y1y2⋮yn)⏟Y(n×1)=(x1,1x1,2⋯x1,nx2,1x2,2⋯x2,n⋮⋮⋱⋮xk,1xk,2⋯xk,n)⏟X(n×k)(β1β2⋮βk)⏟β(k×1)+(u1u2⋮un)⏟u(n×1)

The Multivariate OLS Estimators: FYI

Math FYI: in linear algebra terms, a regression model with n observations of k independent variables:

Y=Xβ+u

(y1y2⋮yn)⏟Y(n×1)=(x1,1x1,2⋯x1,nx2,1x2,2⋯x2,n⋮⋮⋱⋮xk,1xk,2⋯xk,n)⏟X(n×k)(β1β2⋮βk)⏟β(k×1)+(u1u2⋮un)⏟u(n×1)

  • The OLS estimator for β is ˆβ=(X′X)−1X′Y

The Multivariate OLS Estimators: FYI

Math FYI: in linear algebra terms, a regression model with n observations of k independent variables:

Y=Xβ+u

(y1y2⋮yn)⏟Y(n×1)=(x1,1x1,2⋯x1,nx2,1x2,2⋯x2,n⋮⋮⋱⋮xk,1xk,2⋯xk,n)⏟X(n×k)(β1β2⋮βk)⏟β(k×1)+(u1u2⋮un)⏟u(n×1)

  • The OLS estimator for β is ˆβ=(X′X)−1X′Y

  • Appreciate that I am saving you from such sorrow

The Sampling Distribution of ^βj

The Sampling Distribution of ^βj I

  • For any individual βj, it has a sampling distribution:

^βj∼N(E[^βj],se(^βj))

  • We want to know its sampling distribution's:
    • Center: E[^βj]; what is the expected value of our estimator?
    • Spread: se(^βj); how precise is our estimator?

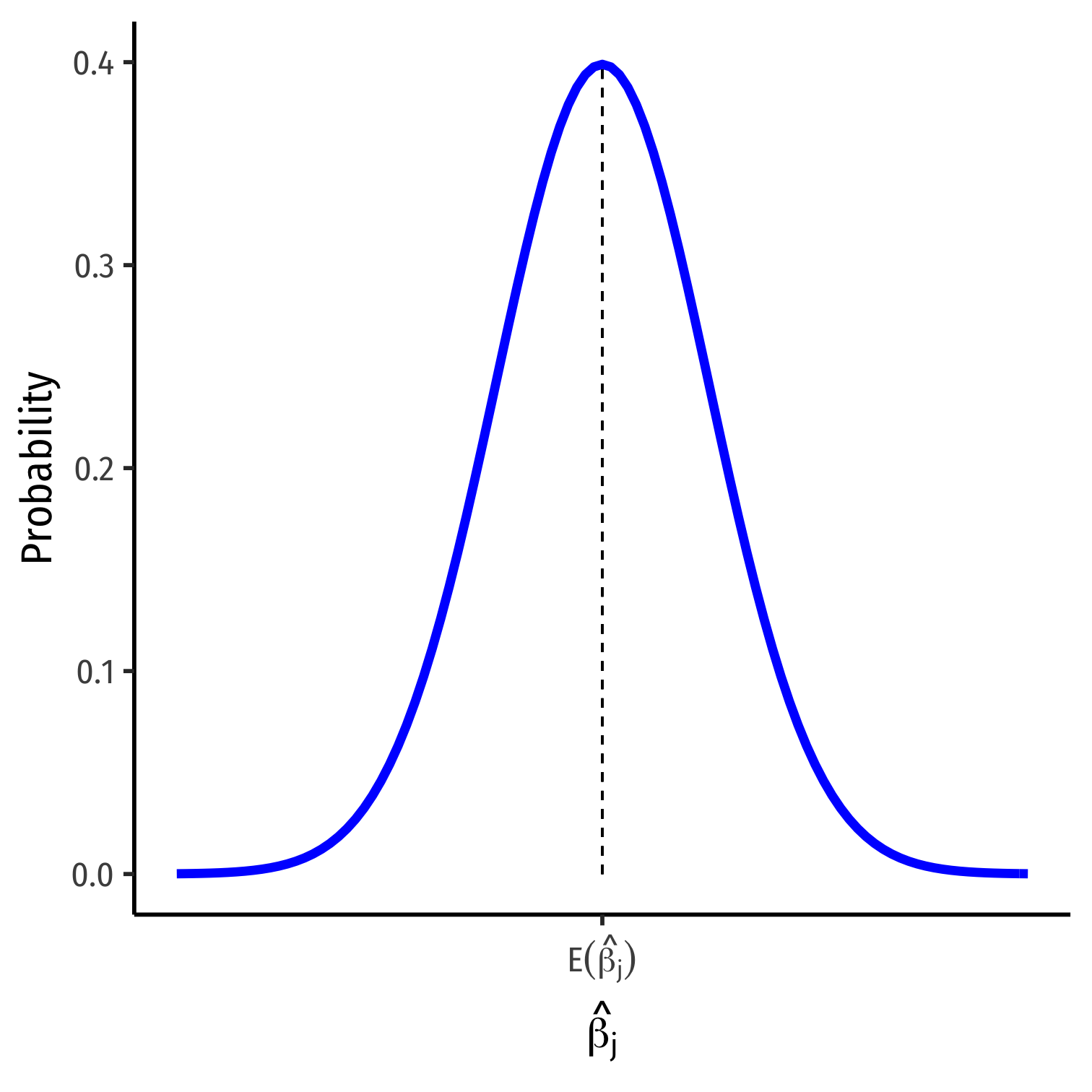
The Expected Value of ^βj: Bias

Exogeneity and Unbiasedness

  • As before, E[^βj]=βj when Xj is exogenous (i.e. cor(Xj,u)=0)

  • We know the true E[^βj]=βj+cor(Xj,u)σuσXj⏟O.V. Bias

  • If Xj is endogenous (i.e. cor(Xj,u)≠0), contains omitted variable bias

  • We can now try to quantify the omitted variable bias

Measuring Omitted Variable Bias I

  • Suppose the true population model of a relationship is:

Yi=β0+β1X1i+β2X2i+ui

  • What happens when we run a regression and omit X2i?

Measuring Omitted Variable Bias I

  • Suppose the true population model of a relationship is:

Yi=β0+β1X1i+β2X2i+ui

  • What happens when we run a regression and omit X2i?

  • Suppose we estimate the following omitted regression of just Yi on X1i (omitting X2i):+

Yi=α0+α1X1i+νi

+ Note: I am using α's and νi only to denote these are different estimates than the true model β's and ui

Measuring Omitted Variable Bias II

  • Key Question: are X1i and X2i correlated?

Measuring Omitted Variable Bias II

  • Key Question: are X1i and X2i correlated?

  • Run an auxiliary regression of X2i on X1i to see:+

X2i=δ0+δ1X1i+τi

Measuring Omitted Variable Bias II

  • Key Question: are X1i and X2i correlated?

  • Run an auxiliary regression of X2i on X1i to see:+

X2i=δ0+δ1X1i+τi

  • If δ1=0, then X1i and X2i are not linearly related

  • If |δ1| is very big, then X1i and X2i are strongly linearly related

+ Note: I am using δ's and τ to differentiate estimates for this model.

Measuring Omitted Variable Bias III

  • Now substitute our auxiliary regression between X2i and X1i into the true model:
    • We know X2i=δ0+δ1X1i+τi

Yi=β0+β1X1i+β2X2i+ui

Measuring Omitted Variable Bias III

  • Now substitute our auxiliary regression between X2i and X1i into the true model:
    • We know X2i=δ0+δ1X1i+τi

Yi=β0+β1X1i+β2X2i+uiYi=β0+β1X1i+β2(δ0+δ1X1i+τi)+ui

Measuring Omitted Variable Bias III

  • Now substitute our auxiliary regression between X2i and X1i into the true model:
    • We know X2i=δ0+δ1X1i+τi

Yi=β0+β1X1i+β2X2i+uiYi=β0+β1X1i+β2(δ0+δ1X1i+τi)+uiYi=(β0+β2δ0)+(β1+β2δ1)X1i+(β2τi+ui)

Measuring Omitted Variable Bias III

  • Now substitute our auxiliary regression between X2i and X1i into the true model:
    • We know X2i=δ0+δ1X1i+τi

Yi=β0+β1X1i+β2X2i+uiYi=β0+β1X1i+β2(δ0+δ1X1i+τi)+uiYi=(β0+β2δ0⏟α0)+(β1+β2δ1⏟α1)X1i+(β2τi+ui⏟νi)

  • Now relabel each of the three terms as the OLS estimates (α's) and error (νi) from the omitted regression, so we again have:

Yi=α0+α1X1i+νi

Measuring Omitted Variable Bias III

  • Now substitute our auxiliary regression between X2i and X1i into the true model:
    • We know X2i=δ0+δ1X1i+τi

Yi=β0+β1X1i+β2X2i+uiYi=β0+β1X1i+β2(δ0+δ1X1i+τi)+uiYi=(β0+β2δ0⏟α0)+(β1+β2δ1⏟α1)X1i+(β2τi+ui⏟νi)

  • Now relabel each of the three terms as the OLS estimates (α's) and error (νi) from the omitted regression, so we again have:

Yi=α0+α1X1i+νi

  • Crucially, this means that our OLS estimate for X1i in the omitted regression is: α1=β1+β2δ1

Measuring Omitted Variable Bias IV

α1=β1 + β2δ1

  • The Omitted Regression OLS estimate for X1i picks up both:

  1. The true effect of X1 on Yi: (β1)

  2. The true effect of X2 on Yi: (β2)

    • As pulled through the relationship between X1 and X2: (δ1)

Measuring Omitted Variable Bias IV

α1=β1 + β2δ1

  • The Omitted Regression OLS estimate for X1i picks up both:

  1. The true effect of X1 on Yi: (β1)

  2. The true effect of X2 on Yi: (β2)

    • As pulled through the relationship between X1 and X2: (δ1)
  • Recall our conditions for omitted variable bias from some variable Zi:

  1. Zi must be a determinant of Yi ⟹ β2≠0

  2. Zi must be correlated with Xi ⟹ δ1≠0

Measuring Omitted Variable Bias IV

α1=β1 + β2δ1

  • The Omitted Regression OLS estimate for X1i picks up both:

  1. The true effect of X1 on Yi: (β1)

  2. The true effect of X2 on Yi: (β2)

    • As pulled through the relationship between X1 and X2: (δ1)
  • Recall our conditions for omitted variable bias from some variable Zi:

  1. Zi must be a determinant of Yi ⟹ β2≠0

  2. Zi must be correlated with Xi ⟹ δ1≠0

  • Otherwise, if Zi does not fit these conditions, α1=β1 and the omitted regression is unbiased!

Measuring Omitted Variable Bias in Our Class Size Example I

## 
## Call:
## lm(formula = testscr ~ str + el_pct, data = CASchool)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -48.845 -10.240  -0.308   9.815  43.461 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 686.03225    7.41131  92.566  < 2e-16 ***
## str          -1.10130    0.38028  -2.896  0.00398 ** 
## el_pct       -0.64978    0.03934 -16.516  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.46 on 417 degrees of freedom
## Multiple R-squared:  0.4264,    Adjusted R-squared:  0.4237 
## F-statistic:   155 on 2 and 417 DF,  p-value: < 2.2e-16
  • The "True" Regression (Yi on X1i and X2i)

^Test Scorei=686.03−1.10 STRi−0.65 %ELi

Measuring Omitted Variable Bias in Our Class Size Example II

## 
## Call:
## lm(formula = testscr ~ str, data = CASchool)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -47.727 -14.251   0.483  12.822  48.540 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 698.9330     9.4675  73.825  < 2e-16 ***
## str          -2.2798     0.4798  -4.751 2.78e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 18.58 on 418 degrees of freedom
## Multiple R-squared:  0.05124,    Adjusted R-squared:  0.04897 
## F-statistic: 22.58 on 1 and 418 DF,  p-value: 2.783e-06
  • The "Omitted" Regression (Yi on just X1i)

^Test Scorei=698.93−2.28 STRi

Measuring Omitted Variable Bias in Our Class Size Example III

## 
## Call:
## lm(formula = el_pct ~ str, data = CASchool)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -20.823 -13.006  -6.849   7.834  74.601 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -19.8541     9.1626  -2.167  0.03081 *  
## str           1.8137     0.4644   3.906  0.00011 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 17.98 on 418 degrees of freedom
## Multiple R-squared:  0.03521,    Adjusted R-squared:  0.0329 
## F-statistic: 15.25 on 1 and 418 DF,  p-value: 0.0001095
  • The "Auxiliary" Regression (X2i on X1i)

^%ELi=−19.85+1.81 STRi

Measuring Omitted Variable Bias in Our Class Size Example IV

"True" Regression

^Test Scorei=686.03−1.10 STRi−0.65 %EL

"Omitted" Regression

^Test Scorei=698.93 −2.28  STRi

"Auxiliary" Regression

^%ELi=−19.85+1.81 STRi

  • Omitted Regression estimate for α1 on STR is −2.28

Measuring Omitted Variable Bias in Our Class Size Example IV

"True" Regression

^Test Scorei=686.03 −1.10  STRi−0.65 %EL

"Omitted" Regression

^Test Scorei=698.93 −2.28  STRi

"Auxiliary" Regression

^%ELi=−19.85+1.81 STRi

  • Omitted Regression estimate for α1 on STR is −2.28

α1=β1 + β2δ1

  • The true effect of STR on Test Score: -1.10

Measuring Omitted Variable Bias in Our Class Size Example IV

"True" Regression

^Test Scorei=686.03 −1.10  STRi −0.65  %EL

"Omitted" Regression

^Test Scorei=698.93 −2.28  STRi

"Auxiliary" Regression

^%ELi=−19.85+1.81 STRi

  • Omitted Regression estimate for α1 on STR is −2.28

α1=β1 + β2δ1

  • The true effect of STR on Test Score: -1.10

  • The true effect of %EL on Test Score: -0.65

Measuring Omitted Variable Bias in Our Class Size Example IV

"True" Regression

^Test Scorei=686.03 −1.10  STRi −0.65  %EL

"Omitted" Regression

^Test Scorei=698.93 −2.28  STRi

"Auxiliary" Regression

^%ELi=−19.85+ 1.81  STRi

  • Omitted Regression estimate for α1 on STR is −2.28

α1=β1 + β2δ1

  • The true effect of STR on Test Score: -1.10

  • The true effect of %EL on Test Score: -0.65

  • The relationship between STR and %EL: 1.81

Measuring Omitted Variable Bias in Our Class Size Example IV

"True" Regression

^Test Scorei=686.03 −1.10  STRi −0.65  %EL

"Omitted" Regression

^Test Scorei=698.93 −2.28  STRi

"Auxiliary" Regression

^%ELi=−19.85+ 1.81  STRi

  • Omitted Regression estimate for α1 on STR is −2.28

α1=β1 + β2δ1

  • The true effect of STR on Test Score: -1.10

  • The true effect of %EL on Test Score: -0.65

  • The relationship between STR and %EL: 1.81

  • So, for the omitted regression:

α1=−2.28 =−1.10 + −0.65 ( 1.81 )

Measuring Omitted Variable Bias in Our Class Size Example IV

"True" Regression

^Test Scorei=686.03 −1.10  STRi −0.65  %EL

"Omitted" Regression

^Test Scorei=698.93 −2.28  STRi

"Auxiliary" Regression

^%ELi=−19.85+ 1.81  STRi

  • Omitted Regression estimate for α1 on STR is −2.28

α1=β1 + β2δ1

  • The true effect of STR on Test Score: -1.10

  • The true effect of %EL on Test Score: -0.65

  • The relationship between STR and %EL: 1.81

  • So, for the omitted regression:

α1=−2.28 =−1.10 + −0.65 ( 1.81 )

  • The bias is ( −0.65 )( 1.81 )=−1.18

Precision of ^βj

Precision of ^βj I

  • σ^βj; how precise are our estimates? (today)
    • Variance σ2^βj or standard error σ^βj

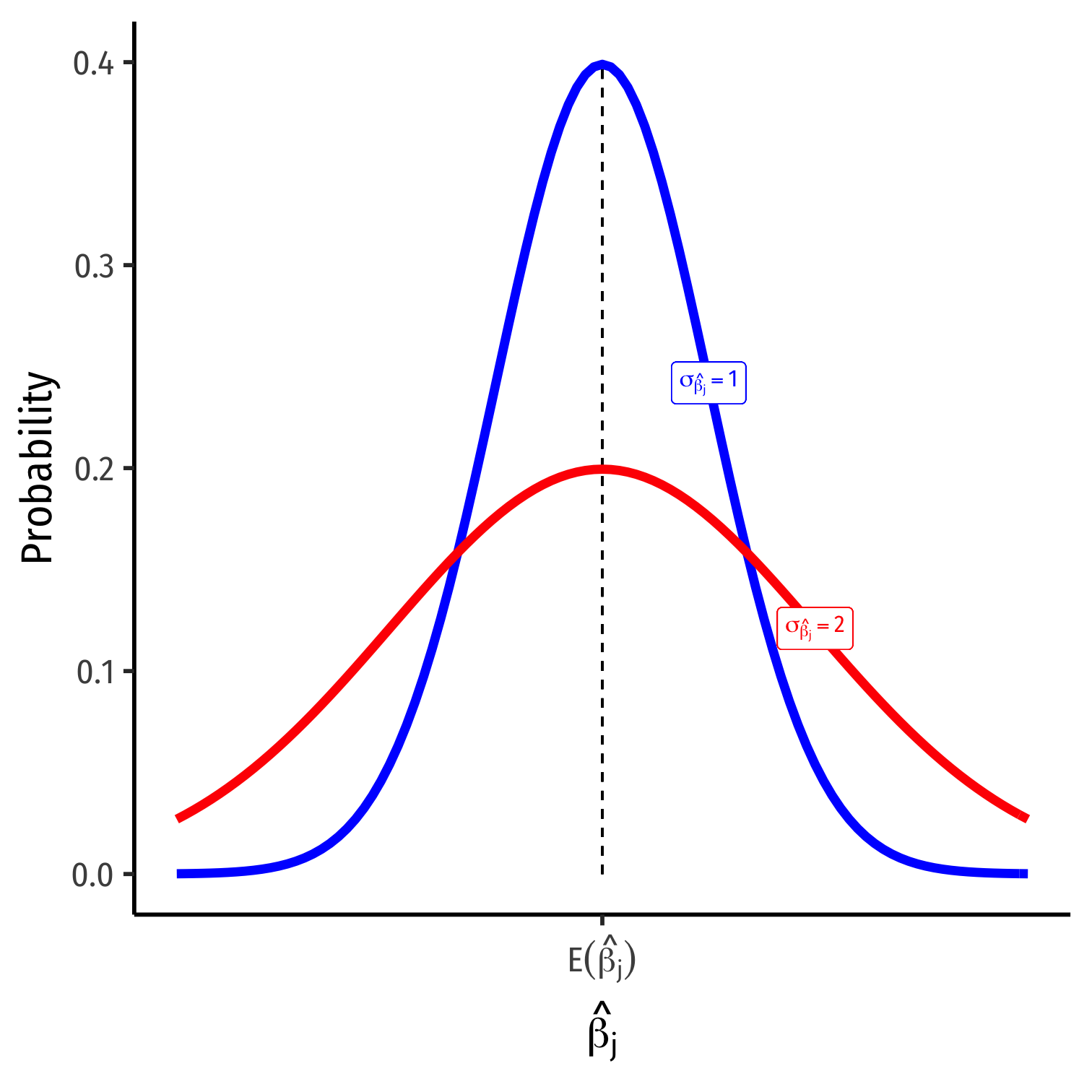
Precision of ^βj II

var(^βj)=11−R2j⏟VIF×(SER)2n×var(X)

se(^βj)=√var(^β1)

  • Variation in ^βj is affected by four things now:
  1. Goodness of fit of the model (SER)
    • Larger SER → larger var(^βj)
  2. Sample size, n
    • Larger n → smaller var(^βj)
  3. Variance of X
    • Larger var(X) → smaller var(^βj)
  4. Variance Inflation Factor 1(1−R2j)
    • Larger VIF, larger var(^βj)
    • This is the only new effect, explained in a moment

+ See Class 2.5 for a reminder of variation with just variable.

VIF and Multicollinearity I

  • Two independent variables are multicollinear:

cor(Xj,Xl)≠0∀j≠l

VIF and Multicollinearity I

  • Two independent variables are multicollinear:

cor(Xj,Xl)≠0∀j≠l

  • Multicollinearity between X variables does not bias OLS estimates
    • Remember, we pulled another variable out of u into the regression
    • If it were omitted, then it would cause omitted variable bias!

VIF and Multicollinearity I

  • Two independent variables are multicollinear:

cor(Xj,Xl)≠0∀j≠l

  • Multicollinearity between X variables does not bias OLS estimates

    • Remember, we pulled another variable out of u into the regression
    • If it were omitted, then it would cause omitted variable bias!

  • Multicollinearity does increase the variance of an estimate by

VIF=1(1−R2j)

VIF and Multicollinearity II

VIF=1(1−R2j)

  • R2j is the R2 from an auxiliary regression of Xj on all other regressors (X's)

VIF and Multicollinearity II

VIF=1(1−R2j)

  • R2j is the R2 from an auxiliary regression of Xj on all other regressors (X's)

Example: Suppose we have a regression with three regressors (k=3):

Yi=β0+β1X1i+β2X2i+β3X3i

VIF and Multicollinearity II

VIF=1(1−R2j)

  • R2j is the R2 from an auxiliary regression of Xj on all other regressors (X's)

Example: Suppose we have a regression with three regressors (k=3):

Yi=β0+β1X1i+β2X2i+β3X3i

  • There will be three different R2j's, one for each regressor:

R21 for X1i=γ+γX2i+γX3iR22 for X2i=ζ0+ζ1X1i+ζ2X3iR23 for X3i=η0+η1X1i+η2X2i

VIF and Multicollinearity III

VIF=1(1−R2j)

  • R2j is the R2 from an auxiliary regression of Xj on all other regressors (X's)

  • The R2j tells us how much other regressors explain regressor Xj

  • Key Takeaway: If other X variables explain Xj well (high R2J), it will be harder to tell how cleanly Xj→Yi, and so var(^βj) will be higher

VIF and Multicollinearity IV

  • Common to calculate the Variance Inflation Factor (VIF) for each regressor:

VIF=1(1−R2j)

  • VIF quantifies the factor (scalar) by which var(^βj) increases because of multicollinearity
    • e.g. increases 2x, 3x, etc.

VIF and Multicollinearity IV

  • Common to calculate the Variance Inflation Factor (VIF) for each regressor:

VIF=1(1−R2j)

  • VIF quantifies the factor (scalar) by which var(^βj) increases because of multicollinearity
    • e.g. increases 2x, 3x, etc.
  • Baseline: R2j=0 ⟹ no multicollinearity ⟹ VIF = 1 (no inflation)

VIF and Multicollinearity IV

  • Common to calculate the Variance Inflation Factor (VIF) for each regressor:

VIF=1(1−R2j)

  • VIF quantifies the factor (scalar) by which var(^βj) increases because of multicollinearity
    • e.g. increases 2x, 3x, etc.

  • Baseline: R2j=0 ⟹ no multicollinearity ⟹ VIF = 1 (no inflation)

  • Larger R2j ⟹ larger VIF

    • Rule of thumb: VIF>10 is worrisome

VIF and Multicollinearity V

ggplot(data=CASchool, aes(x=str,y=el_pct))+
  geom_point(color="blue")+
  geom_smooth(method="lm", color="red")+
  labs(x = "Student to Teacher Ratio",
       y = "Percentage of ESL Students")+
    theme_classic(base_family = "Fira Sans Condensed",
           base_size=20)
CAcorr_ex<-subset(CASchool, select=c("testscr", "str", "el_pct"))
# Make a correlation table
cor(CAcorr_ex)
##            testscr        str     el_pct
## testscr  1.0000000 -0.2263628 -0.6441237
## str     -0.2263628  1.0000000  0.1876424
## el_pct  -0.6441237  0.1876424  1.0000000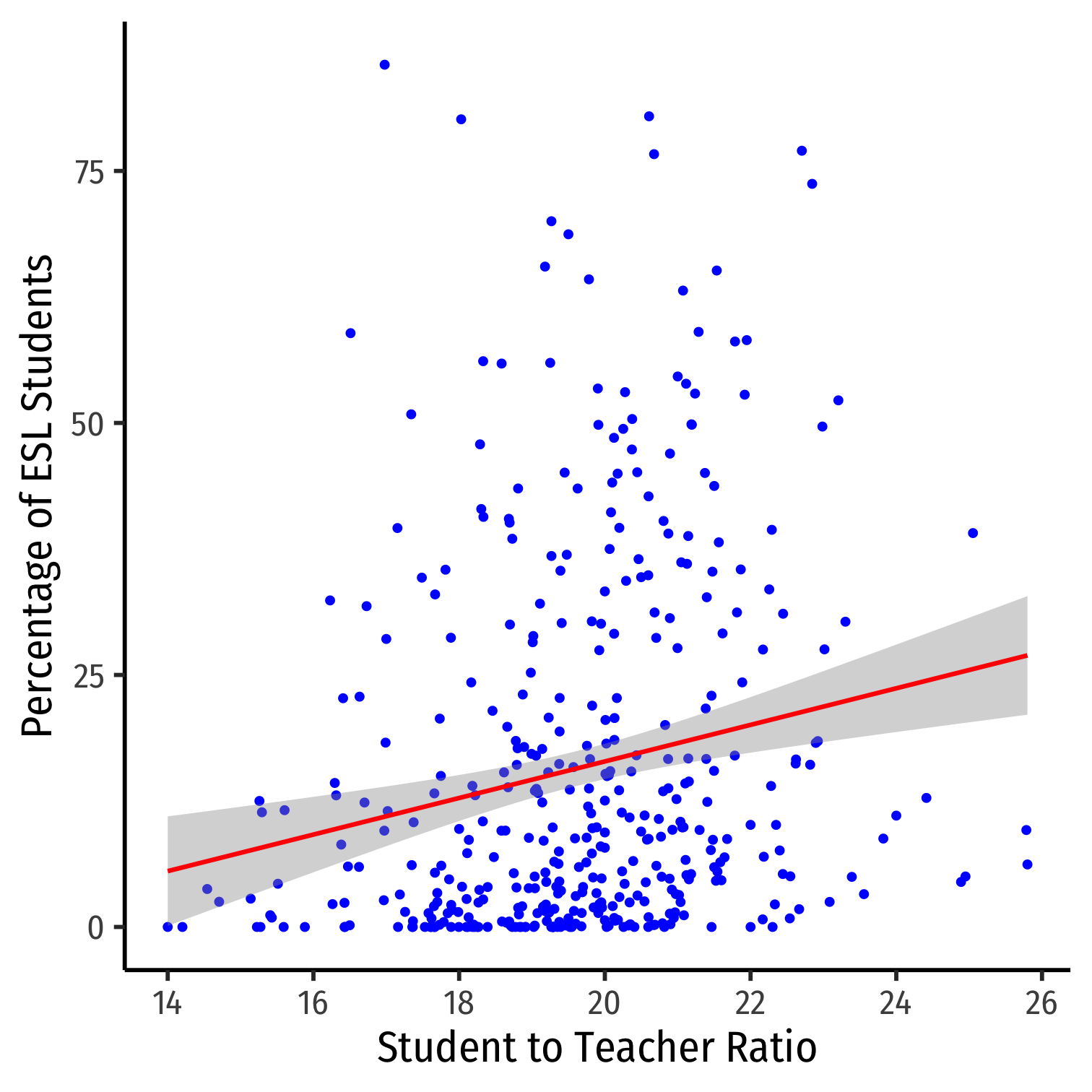

VIF and Multicollinearity in R I

# our multivariate regression
elreg<-lm(testscr~str+el_pct,data=CASchool)
# use the "car" package for VIF function 
library("car") 
# syntax: vif(lm.object)
vif(elreg)
##      str   el_pct 
## 1.036495 1.036495

VIF and Multicollinearity in R I

# our multivariate regression
elreg<-lm(testscr~str+el_pct,data=CASchool)
# use the "car" package for VIF function 
library("car") 
# syntax: vif(lm.object)
vif(elreg)
##      str   el_pct 
## 1.036495 1.036495
  • var(^β1) on str increases by 1.036 times due to multicollinearity with el_pct
  • var(^β2) on el_pct increases by 1.036 times due to multicollinearity with str

VIF and Multicollinearity in R II

  • Let's calculate VIF manually to see where it comes from:

VIF and Multicollinearity in R II

  • Let's calculate VIF manually to see where it comes from:
# run auxiliary regression of x2 on x1
auxreg<-lm(el_pct~str, data=CASchool)
# use broom package's tidy() command (cleaner)
library(broom) # load broom
tidy(auxreg) # look at reg output
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
p.value
<dbl>
(Intercept)-19.8540559.1626044-2.1668570.0308099863
str1.8137190.46437353.9057330.0001095165
2 rows

VIF and Multicollinearity in R III

glance(auxreg) # look at aux reg stats for R^2
ABCDEFGHIJ0123456789
r.squared
<dbl>
adj.r.squared
<dbl>
sigma
<dbl>
statistic
<dbl>
p.value
<dbl>
df
<int>
logLik
<dbl>
AIC
<dbl>
0.035209660.0329015517.9825915.254750.00010951652-1808.5023623.003
1 row | 1-8 of 11 columns
# extract our R-squared from aux regression (R_j^2)
aux_r_squared<-glance(auxreg) %>%
  pull(r.squared)
aux_r_squared # look at it
## [1] 0.03520966

VIF and Multicollinearity in R IV

# calculate VIF manually
our_vif<-1/(1-aux_r_squared) # VIF formula 
our_vif
## [1] 1.036495
  • Again, multicollinearity between the two X variables inflates the variance on each by 1.036 times

VIF and Multicollinearity: Another Example I

Example: For our Test Scores and Class Size example, what about district expenditures per student?

CAcorr2<-subset(CASchool, select=c("testscr", "str", "expn_stu"))
# Make a correlation table
corr2<-cor(CAcorr2)
# look at it
corr2
##             testscr        str   expn_stu
## testscr   1.0000000 -0.2263628  0.1912728
## str      -0.2263628  1.0000000 -0.6199821
## expn_stu  0.1912728 -0.6199821  1.0000000

VIF and Multicollinearity: Another Example II

ggplot(data=CASchool, aes(x=str,y=expn_stu))+
  geom_point(color="blue")+
  geom_smooth(method="lm", color="red")+
  scale_y_continuous(labels = scales::dollar)+
  labs(x = "Student to Teacher Ratio",
       y = "Expenditures per Student ($)")+
    theme_classic(base_family = "Fira Sans Condensed",
           base_size=20)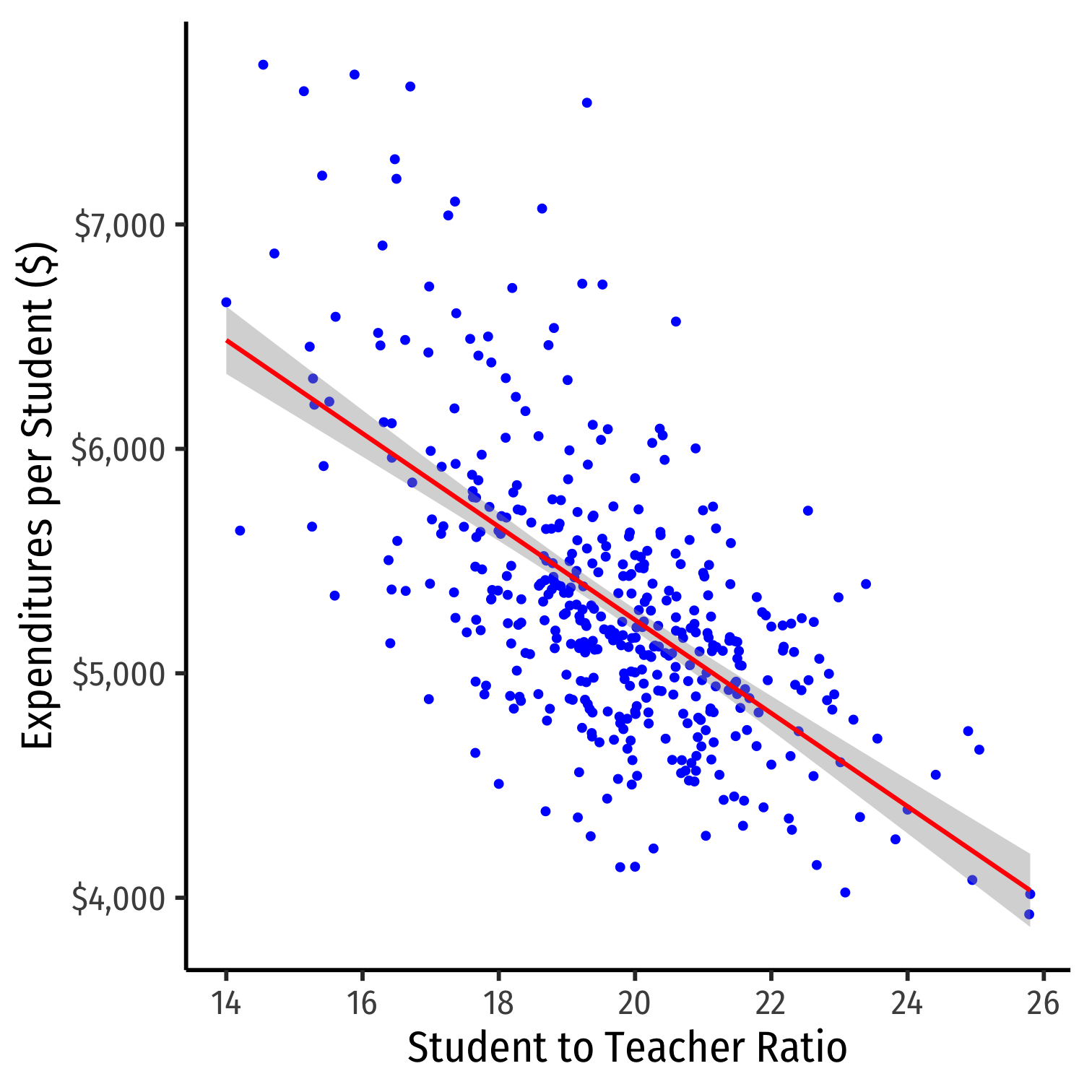

VIF and Multicollinearity: Another Example III

  1. cor(Test score, expn)≠0

  2. cor(STR, expn)≠0

VIF and Multicollinearity: Another Example III

  1. cor(Test score, expn)≠0

  2. cor(STR, expn)≠0

  • Omitting expn will bias ^β1 on STR

VIF and Multicollinearity: Another Example III

  1. cor(Test score, expn)≠0

  2. cor(STR, expn)≠0

  • Omitting expn will bias ^β1 on STR

  • Including expn will not bias ^β1 on STR, but will make it less precise (higher variance)

VIF and Multicollinearity: Another Example III

  1. cor(Test score, expn)≠0

  2. cor(STR, expn)≠0

  • Omitting expn will bias ^β1 on STR

  • Including expn will not bias ^β1 on STR, but will make it less precise (higher variance)

  • Data tells us little about the effect of a change in STR holding expn constant

    • Hard to know what happens to test scores when high STR AND high expn and vice versa (they rarely happen simultaneously)!

VIF and Multicollinearity: Another Example IV

expreg<-lm(testscr~str+expn_stu, data=CASchool)
summary(expreg)
## 
## Call:
## lm(formula = testscr ~ str + expn_stu, data = CASchool)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -47.507 -14.403   0.407  13.195  48.392 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 675.577174  19.562222  34.535   <2e-16 ***
## str          -1.763216   0.610914  -2.886   0.0041 ** 
## expn_stu      0.002487   0.001823   1.364   0.1733    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 18.56 on 417 degrees of freedom
## Multiple R-squared:  0.05545,    Adjusted R-squared:  0.05092 
## F-statistic: 12.24 on 2 and 417 DF,  p-value: 6.824e-06
vif(expreg)
##      str expn_stu 
## 1.624373 1.624373
  • Including expn_stu increases variance of ^β1 by 1.62 times

Multicollinearity Increases Variance

library(huxtable)
huxreg("Model 1" = school_reg,
       "Model 2" = expreg,
       coefs = c("Intercept" = "(Intercept)",
                 "Class Size" = "str",
                 "Expenditures per Student" = "expn_stu"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 2)
  • We can see SE(^β1) on str increases from 0.48 to 0.61 when we add expn_stu
Model 1 Model 2
Intercept 698.93 *** 675.58 ***
(9.47)    (19.56)   
Class Size -2.28 *** -1.76 ** 
(0.48)    (0.61)   
Expenditures per Student         0.00    
        (0.00)   
N 420        420       
R-Squared 0.05     0.06    
SER 18.58     18.56    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Perfect Multicollinearity

  • Perfect multicollinearity is when a regressor is an exact linear function of (an)other regressor(s)

Perfect Multicollinearity

  • Perfect multicollinearity is when a regressor is an exact linear function of (an)other regressor(s)

^Sales=^β0+^β1Temperature (C)+^β2Temperature (F)

Perfect Multicollinearity

  • Perfect multicollinearity is when a regressor is an exact linear function of (an)other regressor(s)

^Sales=^β0+^β1Temperature (C)+^β2Temperature (F)

Temperature (F)=32+1.8∗Temperature (C)

Perfect Multicollinearity

  • Perfect multicollinearity is when a regressor is an exact linear function of (an)other regressor(s)

^Sales=^β0+^β1Temperature (C)+^β2Temperature (F)

Temperature (F)=32+1.8∗Temperature (C)

  • cor(temperature (F), temperature (C))=1

Perfect Multicollinearity

  • Perfect multicollinearity is when a regressor is an exact linear function of (an)other regressor(s)

^Sales=^β0+^β1Temperature (C)+^β2Temperature (F)

Temperature (F)=32+1.8∗Temperature (C)

  • cor(temperature (F), temperature (C))=1

  • R2j=1 is implying VIF=11−1 and var(^βj)=0!

Perfect Multicollinearity

  • Perfect multicollinearity is when a regressor is an exact linear function of (an)other regressor(s)

^Sales=^β0+^β1Temperature (C)+^β2Temperature (F)

Temperature (F)=32+1.8∗Temperature (C)

  • cor(temperature (F), temperature (C))=1

  • R2j=1 is implying VIF=11−1 and var(^βj)=0!

  • This is fatal for a regression

    • A logical impossiblity, always caused by human error

Perfect Multicollinearity: Example

Example:

^TestScorei=^β0+^β1STRi+^β2%EL+^β3%ES

  • %EL: the percentage of students learning English

  • %ES: the percentage of students fluent in English

  • ES=100−EL

  • |cor(ES,EL)|=1

Perfect Multicollinearity Example II

# generate %EF variable from %EL
CASchool_ex <- CASchool %>%
  mutate(ef_pct = 100 - el_pct)
CASchool_ex %>%
  summarize(cor = cor(ef_pct, el_pct))
cor
-1

Perfect Multicollinearity Example III

ggplot(data=CASchool_ex, aes(x=el_pct,y=ef_pct))+
  geom_point(color="blue")+
  scale_y_continuous(labels = scales::dollar)+
  labs(x = "Percent of ESL Students",
       y = "Percent of Non-ESL Students")+
    theme_classic(base_family = "Fira Sans Condensed",
           base_size=20)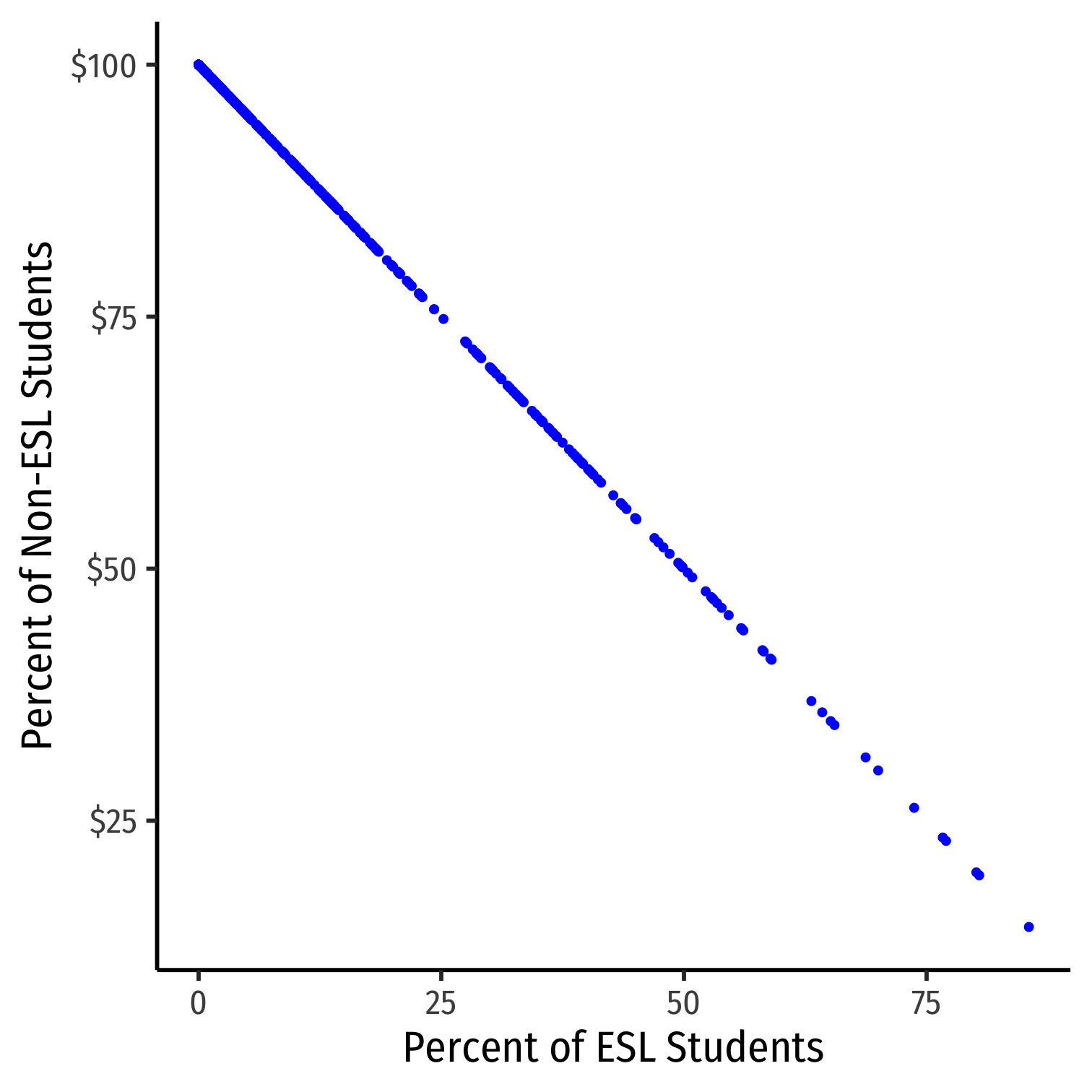

Perfect Multicollinearity Example IV

mcreg<-lm(testscr~str+el_pct+ef_pct, data=CASchool_ex)
summary(mcreg)
## 
## Call:
## lm(formula = testscr ~ str + el_pct + ef_pct, data = CASchool_ex)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -48.845 -10.240  -0.308   9.815  43.461 
## 
## Coefficients: (1 not defined because of singularities)
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 686.03225    7.41131  92.566  < 2e-16 ***
## str          -1.10130    0.38028  -2.896  0.00398 ** 
## el_pct       -0.64978    0.03934 -16.516  < 2e-16 ***
## ef_pct             NA         NA      NA       NA    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.46 on 417 degrees of freedom
## Multiple R-squared:  0.4264,    Adjusted R-squared:  0.4237 
## F-statistic:   155 on 2 and 417 DF,  p-value: < 2.2e-16
  • Note R ignores one of the multicollinear regressors (ef_pct) if you include both in a regression

A Summary of Multivariate OLS Estimator Properties

A Summary of Multivariate OLS Estimator Properties

  • ^βj on Xj is biased only if there is an omitted variable (Z) such that:

    1. cor(Y,Z)≠0
    2. cor(Xj,Z)≠0
    • If Z is included and Xj is collinear with Z, this does not cause a bias

  • var[^βj] and se[^βj] measure precision of estimate:

A Summary of Multivariate OLS Estimator Properties

  • ^βj on Xj is biased only if there is an omitted variable (Z) such that:

    1. cor(Y,Z)≠0
    2. cor(Xj,Z)≠0
    • If Z is included and Xj is collinear with Z, this does not cause a bias

  • var[^βj] and se[^βj] measure precision of estimate:

var[^βj]=1(1−R2j)∗SER2n×var[Xj]

  • VIF from multicollinearity: 1(1−R2j)
    • R2j for auxiliary regression of Xj on all other X's
    • mutlicollinearity does not bias ^βj but raises its variance
    • perfect multicollinearity if X's are linear function of others

Updated Measures of Fit

(Updated) Measures of Fit

  • Again, how well does a linear model fit the data?

  • How much variation in Yi is "explained" by variation in the model ($\hat{Y_i}$)?

(Updated) Measures of Fit

  • Again, how well does a linear model fit the data?

  • How much variation in Yi is "explained" by variation in the model ($\hat{Y_i}$)?

Yi=^Yi+^ui^ui=Yi−^Yi

(Updated) Measures of Fit: SER

  • Again, the Standard errror of the regression (SER) estimates the standard error of u

SER=SSEn−k−1

  • A measure of the spread of the observations around the regression line (in units of Y), the average "size" of the residual

  • Only new change: divided by n−k−1 due to use of k+1 degrees of freedom to first estimate β0 and then all of the other β's for the k number of regressors1

1 Again, because your textbook defines (k) as including the constant, the denominator would be (n-k) instead of (n-k-1).

(Updated) Measures of Fit: R2

R2=ESSTSS=1−SSETSS=(rX,Y)2

  • Again, R2 is fraction of variation of the model (^Yi ("explained SS") to the variation of observations of Yi ("total SS")

(Updated) Measures of Fit: Adjusted ˉR2

  • Problem: R2 of a regression increases every time a new variable is added (it reduces SSE!)

  • This does not mean adding a variable improves the fit of the model per se, R2 gets inflated

(Updated) Measures of Fit: Adjusted ˉR2

  • Problem: R2 of a regression increases every time a new variable is added (it reduces SSE!)

  • This does not mean adding a variable improves the fit of the model per se, R2 gets inflated

  • We correct for this effect with the adjusted R2:

ˉR2=1−n−1n−k−1×SSETSS

  • There are different methods to compute ˉR2, and in the end, recall R2 was never very useful, so don't worry about knowing the formula
    • Large sample sizes (n) make R2 and ˉR2 very close

In R (base)

## 
## Call:
## lm(formula = testscr ~ str + el_pct, data = CASchool)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -48.845 -10.240  -0.308   9.815  43.461 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 686.03225    7.41131  92.566  < 2e-16 ***
## str          -1.10130    0.38028  -2.896  0.00398 ** 
## el_pct       -0.64978    0.03934 -16.516  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.46 on 417 degrees of freedom
## Multiple R-squared:  0.4264,    Adjusted R-squared:  0.4237 
## F-statistic:   155 on 2 and 417 DF,  p-value: < 2.2e-16
  • Base R2 (R calls it multiple R-squared) went up
  • Adjusted R-squared went down

In R (broom)

elreg %>%
  glance()
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC deviance df.residual
0.426 0.424 14.5 155 4.62e-51 3 -1.72e+03 3.44e+03 3.46e+03 8.72e+04 417

The Multivariate OLS Estimators

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow