2.6: Inference for Regression
ECON 480 · Econometrics · Fall 2019
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsf19
metricsF19.classes.ryansafner.com
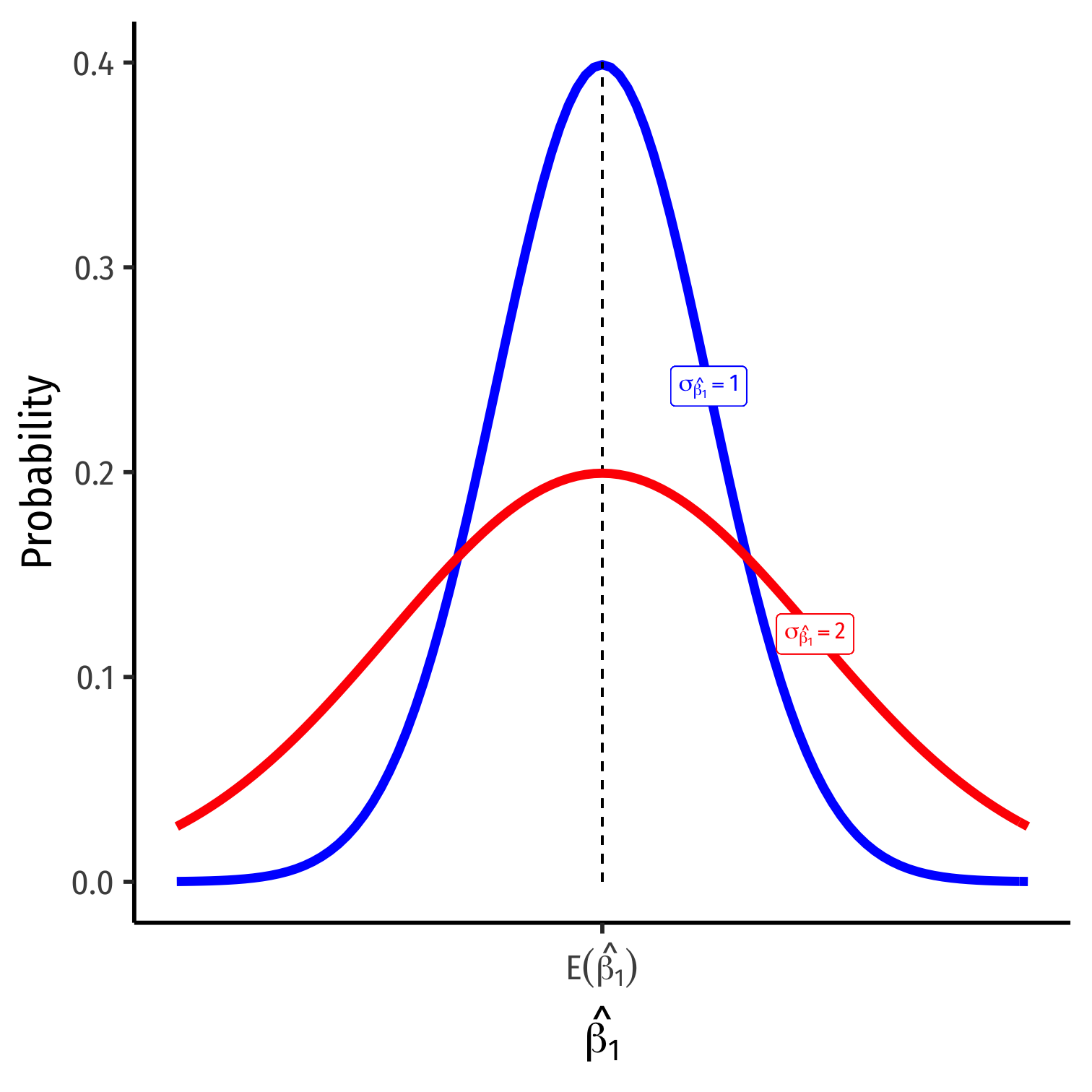
The Sampling Distribution of ^β1
^β1∼N(E[^β1],σ^β1)
E[^β1]; the center of the distribution (2 classes ago)
- E[^β1]=β11
σ^β1; how precise is our estimate? (last class)
- Variance σ2^β1 or standard error σ^β1
1 Under the 4 assumptions about u (particularly, cor(X,u)=0).
Recall: The Two Big Problems with Data
- We use econometrics to identify causal relationships and make inferences about them
Problem for identification: endogeneity
- X is exogenous if its variation is unrelated to other factors (u) that affect Y
- X is endogenous if its variation is related to other factors (u) that affect Y
Problem for inference: randomness
- Data is random due to natural sampling variation
- Taking one sample of a population will yield slightly different information than another sample of the same population


Recall: Distributions of the OLS Estimators
OLS estimators (^β0 and ^β1) are computed from a finite (specific) sample of data
Our OLS model contains 2 sources of randomness:
Recall: Distributions of the OLS Estimators
OLS estimators (^β0 and ^β1) are computed from a finite (specific) sample of data
Our OLS model contains 2 sources of randomness:
Modeled randomness: u includes all factors affecting Y other than X
- different samples will have different values of those other factors (ui)
Recall: Distributions of the OLS Estimators
OLS estimators (^β0 and ^β1) are computed from a finite (specific) sample of data
Our OLS model contains 2 sources of randomness:
Modeled randomness: u includes all factors affecting Y other than X
- different samples will have different values of those other factors (ui)
- Sampling randomness: different samples will generate different OLS estimators
- Thus, ^β0,^β1 are also random variables, with their own sampling distribution
Recall: Inferential Statistics and Sampling Distributions
Inferential statistics analyzes a sample to make inferences about a much larger (unobservable) population
Population: all possible individuals that match some well-defined criterion of interest (people, firms, cities, etc)
- Characteristics about (relationships between variables in) populations are called parameters
Sample: some portion of the population of interest to represent the whole
- Samples generate statistics used to estimate population parameters

Recall: Inference in Econometrics: The Big Picture
Sample→⏟statistical inferencePopulation→⏟causal indentificationUnobserved Parameters
We want to identify causal relationships between population variables
- Logically first thing to consider
- Endogeneity problem
We'll use sample statistics to infer something about population parameters
- In practice, we'll only ever have a finite sample distribution of data
- We don't know the population distribution of data
- Randomness problem
Two Methods of Statistical Inference
- Estimation: use our sample data to construct a point estimate of a population parameter and subject it to a hypothesis test
Two Methods of Statistical Inference
Estimation: use our sample data to construct a point estimate of a population parameter and subject it to a hypothesis test
Confidence interval: use our sample data to construct a range for the population parameter
Two Methods of Statistical Inference
Estimation: use our sample data to construct a point estimate of a population parameter and subject it to a hypothesis test
Confidence interval: use our sample data to construct a range for the population parameter
First method is more common, but second is still widely acknowledged
Both will give you similar results
- Tradeoff of accuracy vs. precision
Note statistical inference is different than causal inference!
Hypothesis Testing
Estimation and Hypothesis Testing I
We have already used statistics to estimate a relationship between X and Y
- OLS estimators ^β0 and ^β1 of the true population β0 and β1
We want to test if these estimates are statistically significant and they describe the population
- This is the "bread and butter" of inferential statistics and the purpose of regression
Estimation and Hypothesis Testing I
We have already used statistics to estimate a relationship between X and Y
- OLS estimators ^β0 and ^β1 of the true population β0 and β1
We want to test if these estimates are statistically significant and they describe the population
- This is the "bread and butter" of inferential statistics and the purpose of regression
Examples:
- Does reducing class size actually improve test scores?
- Do more years of education increase your wages?
- Is the gender wage gap between men and women really $0.77?
Estimation and Hypothesis Testing I
We have already used statistics to estimate a relationship between X and Y
- OLS estimators ^β0 and ^β1 of the true population β0 and β1
We want to test if these estimates are statistically significant and they describe the population
- This is the "bread and butter" of inferential statistics and the purpose of regression
Examples:
- Does reducing class size actually improve test scores?
- Do more years of education increase your wages?
- Is the gender wage gap between men and women really $0.77?
- All modern science is built upon statistical hypothesis testing, so understand it well!
Estimation and Hypothesis Testing II
Note, we can test a lot of hypotheses about a lot of population parameters, e.g.
- A population mean μ
- Example: average height of adults
- A population proportion p
- Example: percent of voters who voted for Trump
- A difference in population means μA−μB
- Example: difference in average wages of men vs. women
- A difference in population proportions pA−pB
- Example: difference in percent of patients reporting symptoms of drug A vs B
- See all the possibilities in glorious detail in today's Class Notes
- A population mean μ
We will focus only on hypotheses about the population regression slope (ˆβ1), i.e. the causal effect1 of X on Y
1 With a model this simple, it's almost certainly not causal, but this is the ultimate direction we are heading...
Null and Alternative Hypotheses I
- All scientific inquiries begin with a null hypothesis (H0) that proposes a specific value of a population parameter
- Notation: add a subscript 0: β1,0 (or μ0, p0, etc)
Null and Alternative Hypotheses I
- All scientific inquiries begin with a null hypothesis (H0) that proposes a specific value of a population parameter
- Notation: add a subscript 0: β1,0 (or μ0, p0, etc)
- We suggest an alternative hypothesis (Ha), often the one we hope to verify
- Note, can be multiple alternative hypotheses: H1,H2,…,Hn
Null and Alternative Hypotheses I
- All scientific inquiries begin with a null hypothesis (H0) that proposes a specific value of a population parameter
- Notation: add a subscript 0: β1,0 (or μ0, p0, etc)
- We suggest an alternative hypothesis (Ha), often the one we hope to verify
- Note, can be multiple alternative hypotheses: H1,H2,…,Hn
- Ask: "Does our data (sample) give us sufficient evidence to reject H0 in favor of Ha?"
- Note: the test is always about H0!
- See if we have sufficient evidence to reject the status quo
Null and Alternative Hypotheses II
- Null hypothesis assigns a value (or a range) to a population parameter
- e.g. β1=2 or β1≤20
- Most common null hypothesis is β1=0 ⟹ X has no effect on Y (no slope for a line)
- Note: always an equality!
Null and Alternative Hypotheses II
- Null hypothesis assigns a value (or a range) to a population parameter
- e.g. β1=2 or β1≤20
- Most common null hypothesis is β1=0 ⟹ X has no effect on Y (no slope for a line)
- Note: always an equality!
- Alternative hypothesis must mathematically contradict the null hypothesis
- e.g. β1≠2 or β1>20 or β1≠0
- Note: always an inequality!
Null and Alternative Hypotheses II
- Null hypothesis assigns a value (or a range) to a population parameter
- e.g. β1=2 or β1≤20
- Most common null hypothesis is β1=0 ⟹ X has no effect on Y (no slope for a line)
- Note: always an equality!
- Alternative hypothesis must mathematically contradict the null hypothesis
- e.g. β1≠2 or β1>20 or β1≠0
- Note: always an inequality!
- Alternative hypotheses come in two forms:
- One-sided alternative: β1>H0 or β1<H0
- Two-sided alternative: β1≠H0
- Note this means either β1<H0 or β1>H0
Components of a Valid Hypothesis Test
- All statistical hypothesis tests have the following components:
A null hypothesis, H0
An alternative hypothesis, Ha
A test statistic to determine if we reject H0 when the statistic reaches a "critical value"
- Beyond the critical value is the "rejection region", sufficient evidence to reject H0
A conclusion whether or not to reject H0 in favor of Ha
Type I and Type II Errors I
Any sample statistic (e.g. ^β1) will rarely be exactly equal to the hypothesized population parameter (e.g. β1)
Difference between observed statistic and true paremeter could be because:
Parameter is not the hypothesized value (H0 is false)
Parameter is truly the hypothesized value (H0 is true) but sampling variability gave us a different estimate
- We cannot distinguish between these two possibilities with any certainty

Type I and Type II Errors II
- We can interpret our estimates probabilistically as commiting one of two types of error:
Type I error (false positive): rejecting H0 when it is in fact true
- Believing we found an important result when there is truly no relationship
Type II error (false negative): failing to reject H0 when it is in fact false
- Believing we found nothing when there was truly a relationship to find

Type I and Type II Errors III
Truth |
|||
|---|---|---|---|
| Null is True | Null is False | ||
| Judgment | Reject Null | TYPE I ERROR | CORRECT |
| (False +) | (True +) | ||
| Don't Reject Null | CORRECT | TYPE II ERROR | |
| (True -) | (False -) | ||
- Depending on context, committing one type of error may be more serious than the other
Type I and Type II Errors IV
Truth |
|||
|---|---|---|---|
| Defendant is Innocent | Defendant is Guilty | ||
| Judgment | Convict | TYPE I ERROR | CORRECT |
| (False +) | (True +) | ||
| Acquit | CORRECT | TYPE II ERROR | |
| (True -) | (False -) | ||
- Anglo-American common law presumes defendant is innocent: H0
Type I and Type II Errors IV
Truth |
|||
|---|---|---|---|
| Defendant is Innocent | Defendant is Guilty | ||
| Judgment | Convict | TYPE I ERROR | CORRECT |
| (False +) | (True +) | ||
| Acquit | CORRECT | TYPE II ERROR | |
| (True -) | (False -) | ||
Anglo-American common law presumes defendant is innocent: H0
Jury judges whether the evidence presented against the defendant is plausible assuming the defendant were in fact innocent
Type I and Type II Errors IV
Truth |
|||
|---|---|---|---|
| Defendant is Innocent | Defendant is Guilty | ||
| Judgment | Convict | TYPE I ERROR | CORRECT |
| (False +) | (True +) | ||
| Acquit | CORRECT | TYPE II ERROR | |
| (True -) | (False -) | ||
Anglo-American common law presumes defendant is innocent: H0
Jury judges whether the evidence presented against the defendant is plausible assuming the defendant were in fact innocent
If highly improbable: sufficient evidence to reject H0 and convict
- Beyond a "reasonable doubt" that the defendant is innocent
Type I and Type II Errors V

William Blackstone
(1723-1780)
"It is better that ten guilty persons escape than that one innocent suffer."
- Type I error is worse than a Type II error in law!
Blackstone, William, 1765-1770, Commentaries on the Laws of England
Type I and Type II Errors VI

Significance Level, α, and Confidence Level 1−α
- The significance level, α, is the probability of a Type I error
α=P(Reject H0|H0 is true)
Significance Level, α, and Confidence Level 1−α
- The significance level, α, is the probability of a Type I error
α=P(Reject H0|H0 is true)
- The confidence level is defined as (1−α)
- Specify in advance an α-level (0.10, 0.05, 0.01) with associated confidence level (90%, 95%, 99%)
Significance Level, α, and Confidence Level 1−α
- The significance level, α, is the probability of a Type I error
α=P(Reject H0|H0 is true)
The confidence level is defined as (1−α)
- Specify in advance an α-level (0.10, 0.05, 0.01) with associated confidence level (90%, 95%, 99%)
The probability of a Type II error is defined as β:
β=P(Don't reject H0|H0 is false)
α and β
Truth |
|||
|---|---|---|---|
| Null is True | Null is False | ||
| Judgment | Reject Null | TYPE I ERROR | CORRECT |
| (alpha) | (1-beta) | ||
| Don't Reject Null | CORRECT | TYPE II ERROR | |
| (1-alpha) | (beta) | ||
Power and p-values
- The statistical power of the test is (1−β): the probability of correctly rejecting H0 when H0 is in fact false (e.g. not convicting an innocent person)
Power=1−β=P(Reject H0|H0 is false)
Power and p-values
- The statistical power of the test is (1−β): the probability of correctly rejecting H0 when H0 is in fact false (e.g. not convicting an innocent person)
Power=1−β=P(Reject H0|H0 is false)
- The p-value or significance probability is the probability that, given the null hypothesis is true, the test statistic from a random sample will be at least as extreme as the test statistic of our sample
p(δ≥δi|H0 is true)
- where δ represents some test statistic
- δi is the test statistic we observe in our sample
- More on this in a bit
p-Values and Statistical Significance
After running our test, we need to make a decision between the competing hypotheses
Compare p-value with pre-determined α (commonly, α=0.05, 95% confidence level)
- If p<α: statistically significant evidence sufficient to reject H0 in favor of Ha
- If p≥α: insufficient evidence to reject H0
- Note this does not mean H0 is true! We merely have failed to reject H0
Digression: p-Values and the Philosophy of Science
Hypothesis Testing and the Philosophy of Science I

Sir Ronald A. Fisher
(1890—1962)
"The null hypothesis is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis."
1931, The Design of Experiments
Hypothesis Testing and the Philosophy of Science I
Modern philosophy of science is largely based off of hypothesis testing and falsifiability, which form the "Scientific Method"1
For something to be "scientific", it must be falsifiable, or at least testable
Hypotheses can be corroborated with evidence, but always tentative until falsified by data in suggesting an alternative hypothesis
"All swans are white" is a hypothesis rejected upon discovery of a single black swan

Hypothesis Testing and p-Values
- Hypothesis testing, confidence intervals, and p-values are probably the hardest thing to understand in statistics
Hypothesis Testing: Which Test? I
Rigorous course on statistics (ECMG 212 or MATH 112) will spend weeks going through different types of tests:
- Sample mean; difference of means
- Proportion; difference of proportions
- Z-test vs t-test
- 1 sample vs. 2 samples
- χ2 test
See today's class notes page for more
Hypothesis Testing: Which Test? II

There is Only One Test
- Fortunately, some clever statisticians realized "there is only one test" and built a nice
Rpackage calledinfer
Calculate a statistic, δi1, from a sample of data
Simulate a world where δ is null (H0)
Examine the distribution of δ across the null world
Calculate the probability that δi could exist in the null world
Decide if δi is statistically significant
1 δ can stand in for any test-statistic in any hypothesis test! For our purposes, δ is the slope of our regression sample, ˆβ1.
Hypothesis Testing with the infer Package I
- R naturally runs the following hypothesis test on any regression as part of
lm():
H0:β1=0H1:β1≠0
inferallows you to run through these steps manually to understand the process:
Hypothesis Testing with the infer Package I
- R naturally runs the following hypothesis test on any regression as part of
lm():
H0:β1=0H1:β1≠0
inferallows you to run through these steps manually to understand the process:
specify()a model
Hypothesis Testing with the infer Package I
- R naturally runs the following hypothesis test on any regression as part of
lm():
H0:β1=0H1:β1≠0
inferallows you to run through these steps manually to understand the process:
specify()a modelhypothesize()the null
Hypothesis Testing with the infer Package I
- R naturally runs the following hypothesis test on any regression as part of
lm():
H0:β1=0H1:β1≠0
inferallows you to run through these steps manually to understand the process:
specify()a modelhypothesize()the nullgenerate()simulations of the null world
Hypothesis Testing with the infer Package I
- R naturally runs the following hypothesis test on any regression as part of
lm():
H0:β1=0H1:β1≠0
inferallows you to run through these steps manually to understand the process:
specify()a modelhypothesize()the nullgenerate()simulations of the null worldcalculate()the p-value
Hypothesis Testing with the infer Package I
- R naturally runs the following hypothesis test on any regression as part of
lm():
H0:β1=0H1:β1≠0
inferallows you to run through these steps manually to understand the process:
specify()a modelhypothesize()the nullgenerate()simulations of the null worldcalculate()the p-valuevisualize()with a histogram (optional)
Hypothesis Testing with the infer Package II

Hypothesis Testing with the infer Package II

Hypothesis Testing with the infer Package II

Hypothesis Testing with the infer Package II

Hypothesis Testing with the infer Package II

Hypothesis Testing with the infer Package II

Classical Statistical Inference: Critical Values of Test Statistic
Test statistic (δ): measures how far what we observed in our sample (^β1) is from what we would expect if the null hypothesis were true (β1=0)
- Calculated from a sampling distribution of the estimator (i.e. ^β1)
- In econometrics, we use t-distributions which have n−k−1 degrees of freedom.red[1]
Rejection region: if the test statistic reaches a "critical value" of δ, then we reject the null hypothesis
1 Again, see today's class notes for more on the t-distribution. k is the number of independent variables our model has, in this case, with just one X, k=1. We use two degrees of freedom to calculate ^β0 and ^β1, hence we have n−2 df.
Simulating the Sampling Distribution with infer
Imagine a Null World, where H0 is True

Our world, and a world where β1=0 by assumption.
Comparing the Worlds I
- From that null world where H0:β1=0 is true, we simulate another sample and calculate OLS estimators again
Comparing the Worlds I
- From that null world where H0:β1=0 is true, we simulate another sample and calculate OLS estimators again
Our Sample
| ABCDEFGHIJ0123456789 |
term <chr> | estimate <dbl> | std.error <dbl> | |
|---|---|---|---|
| (Intercept) | 698.932952 | 9.4674914 | |
| str | -2.279808 | 0.4798256 |
Comparing the Worlds I
- From that null world where H0:β1=0 is true, we simulate another sample and calculate OLS estimators again
Our Sample
| ABCDEFGHIJ0123456789 |
term <chr> | estimate <dbl> | std.error <dbl> | |
|---|---|---|---|
| (Intercept) | 698.932952 | 9.4674914 | |
| str | -2.279808 | 0.4798256 |
Another Sample
| ABCDEFGHIJ0123456789 |
term <chr> | estimate <dbl> | std.error <dbl> | |
|---|---|---|---|
| (Intercept) | 647.8027952 | 9.7147718 | |
| str | 0.3235038 | 0.4923581 |
Comparing the Worlds II
- From that null world where H0:β1=0 is true, let's simulate 1,000 samples and calculate slope (^β1) for each
Prepping the infer Pipeline
- Before I show you how to do this, let's first save our estimated slope from our actual sample
- We'll want this later!
# save as obs_slopesample_slope <- school_reg_tidy %>% # this is the regression tidied with broom filter(term=="str") %>% pull(estimate)# confirm what it issample_slope## [1] -2.279808The infer Pipeline: Specify

The infer Pipeline: Specify
Specify
data %>% specify(y ~ x)- Take our data and pipe it into the
specify()function, which is essentially alm()function for regression (for our purposes)
CASchool %>% specify(testscr ~ str)| ABCDEFGHIJ0123456789 |
testscr <dbl> | str <dbl> | |||
|---|---|---|---|---|
| 690.8 | 17.88991 | |||
| 661.2 | 21.52466 | |||
| 643.6 | 18.69723 |
- Note nothing happens yet
The infer Pipeline: Hypothesize

The infer Pipeline: Hypothesize
Specify
Hypothesize
%>% hypothesize(null = "independence")- Describe what the null hypothesis is here
- In
infer's language, we are hypothesizing thatstrandtestscrareindependent(β1=0)1
CASchool %>% specify(testscr ~ str) %>% hypothesize(null = "independence")| ABCDEFGHIJ0123456789 |
testscr <dbl> | str <dbl> | |||
|---|---|---|---|---|
| 690.8 | 17.88991 | |||
| 661.2 | 21.52466 | |||
| 643.6 | 18.69723 |
1 type can be either point (for specific point estimates for a single variable, such as a sample mean, (ˉx), or independence (for hypotheses about two samples or a relationship between variables). See more here.
The infer Pipeline: Generate I

The infer Pipeline: Generate I
Specify
Hypothesize
Generate
%>% generate(reps = n, type = "permute")- Now the magic starts, as we run a number of simulated samples1
- Set the number of
repsand set thetypeequal to"permute"
i %>% generate(reps = 1000, type = "permute")1 Note for spacing on the slide, I saved the previous code as i and pipe it into the remainder.
The infer Pipeline: Generate II
Specify
Hypothesize
Generate
%>% generate(reps = n, type = "permute")The infer Pipeline: Generate III
Specify
Hypothesize
Generate
%>% generate(reps = n, type = "permute")- There are two types of simulations we can run:1
"bootstrap"takes a random draw of our existing sample's observations (of the same number of observations) with replacement- this approximates a sampling distribution
"permute"is abootstrapwithout replacement
1 You can do either of these in base R with sample(), which has 3 arguments: a vector to sample from, size (number of obs), and replace equal to TRUE or FALSE. See more for infer here.
The infer Pipeline: Calculate I

The infer Pipeline: Calculate I
Specify
Hypothesize
Generate
Calculate
%>% calculate(stat = "")We
calculatesample statistics for each of the 1,000replicatesamplesIn our case, calculate the slope, (^β1) for each
replicate
i %>% generate(reps = 1000, type = "permute") %>% calculate(stat = "slope")- Other
stats for calculation:"mean","median","prop","diff in means","diff in props", etc. (see package information)
The infer Pipeline: Calculate II
Specify
Hypothesize
Generate
Calculate
%>% calculate(stat = "")The infer Pipeline: Get p Value
Specify
Hypothesize
Generate
Calculate
Get p Value
%>% get_p_value(obs stat = "", direction = "both")We can calculate the p-value
- the probability of seeing a value at least as large as our
sample_slope(-2.28) in our simulated null distribution
- the probability of seeing a value at least as large as our
Two-sided alternative Ha:β1≠0, we double the raw p-value
simulations %>% get_p_value(obs_stat = sample_slope, direction = "both")| ABCDEFGHIJ0123456789 |
p_value <dbl> | ||||
|---|---|---|---|---|
| 0 |
+ Note here I saved the results of our previous code as simulations for spacing.
The infer Pipeline: Get Confidence Interval
Specify
Hypothesize
Generate
Calculate
Get confidence interval
%>% get_ci( level = 0.95, type = "se", point_estimate = "")- We can calculate the confidence interval for β1 from our
sample_slope^β1 of -2.28- CI0.95=^β1±2×se(^β1)
- Specify confidence level (1−α), often 0.95
- Supply our original estimate for
point_estimate
simulations %>% get_confidence_interval(level = 0.95, type = "se", point_estimate = sample_slope)| ABCDEFGHIJ0123456789 |
lower <dbl> | upper <dbl> | |||
|---|---|---|---|---|
| -3.234823 | -1.324793 |
The infer Pipeline: Visualize I

The infer Pipeline: Visualize I
Specify
Hypothesize
Generate
Calculate
Visualize
%>% visualize()- Make a histogram of our null distribution of β1
- Note it is centered at β1=0 because that's H0!
simulations %>% visualize()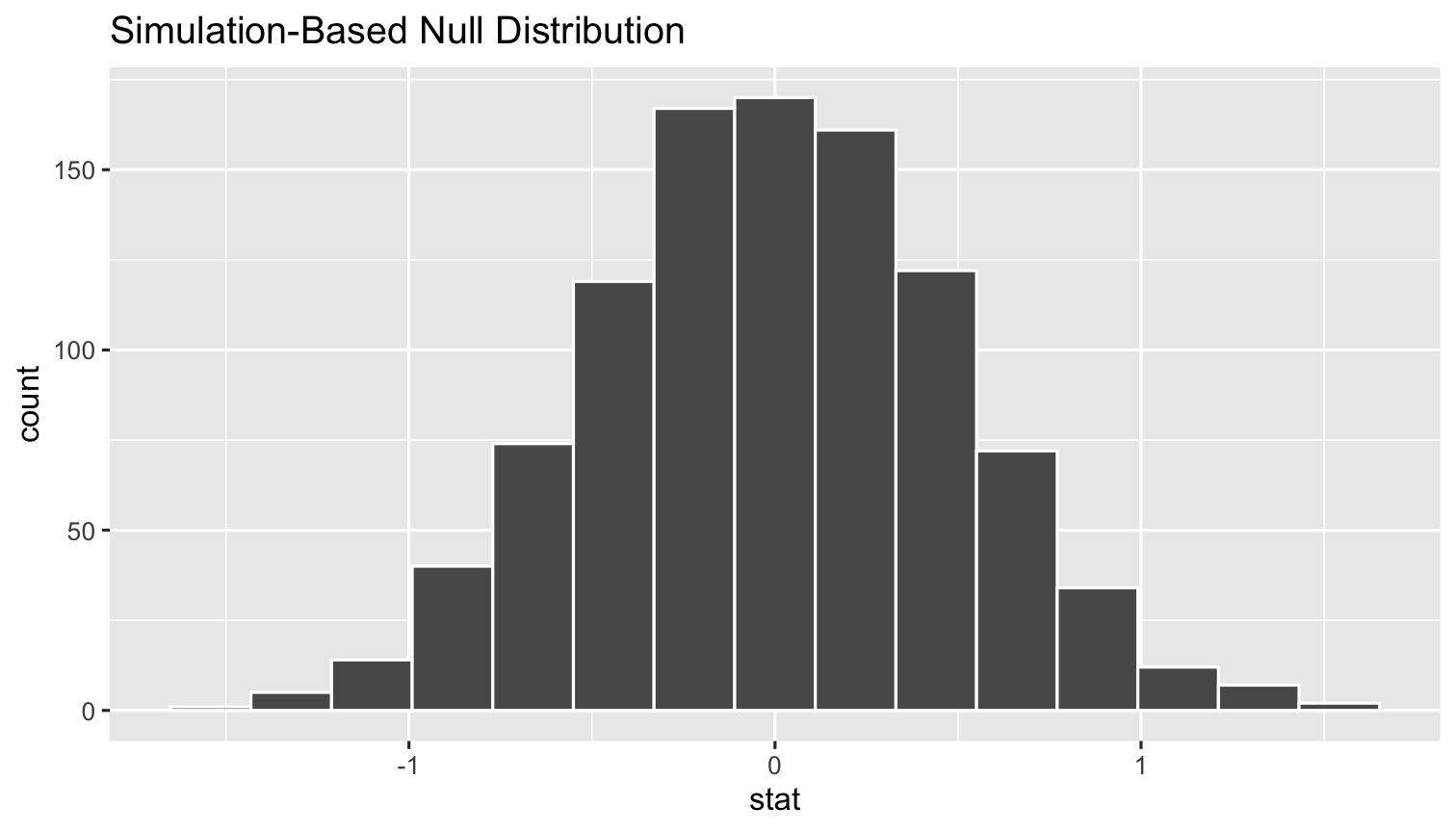
The infer Pipeline: Visualize II
Specify
Hypothesize
Generate
Calculate
Visualize
%>% visualize()- Add our
sample_slopeto show our finding on the null distr.
simulations %>% visualize(obs_stat = sample_slope)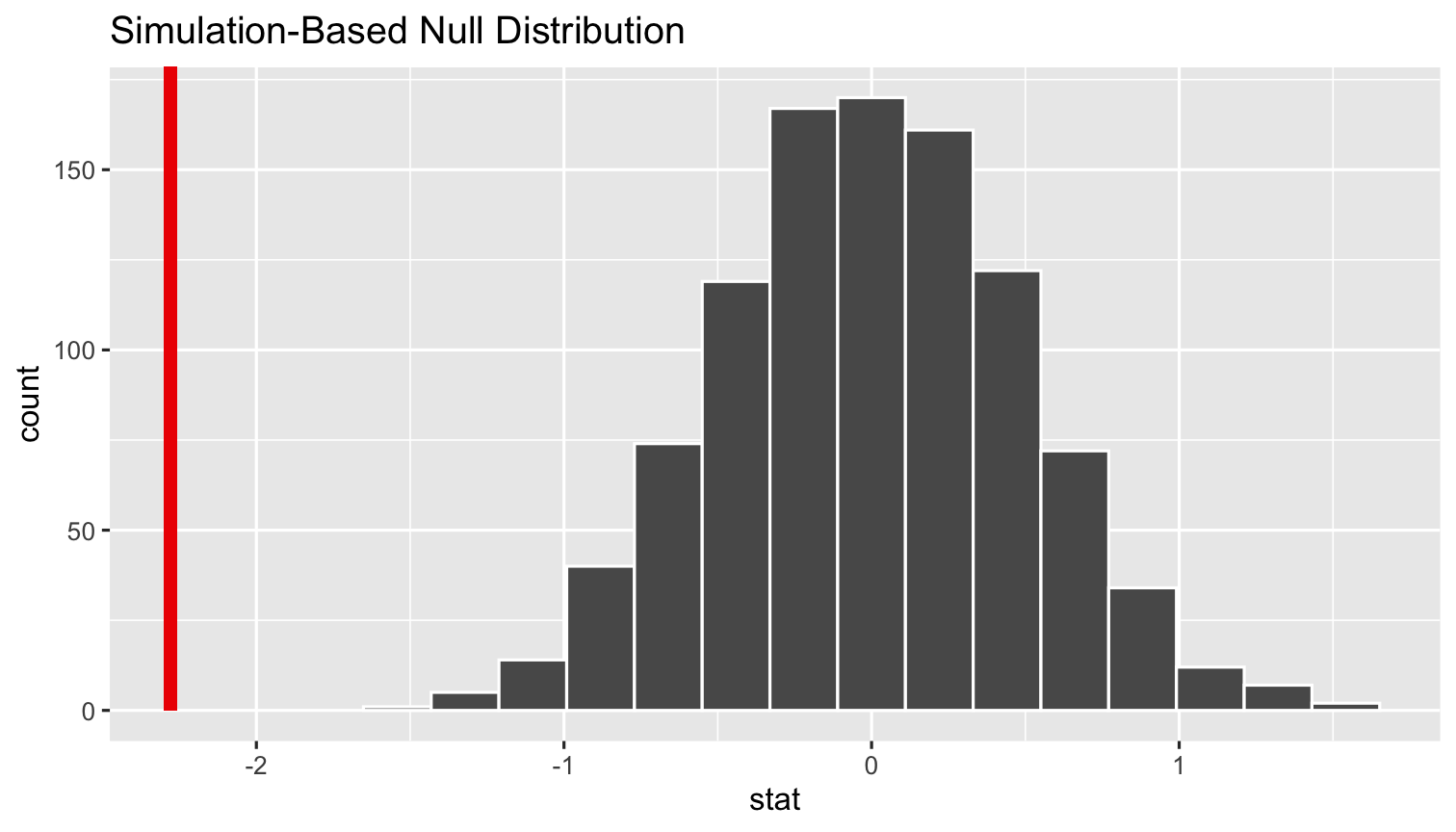
The infer Pipeline: Visualize p-value
Specify
Hypothesize
Generate
Calculate
Visualize
%>% visualize()+ shade_p_value()- Add
shade_p_valueto see what p is
simulations %>% visualize(obs_stat = sample_slope)+ shade_p_value(obs_stat = sample_slope, direction = "two_sided")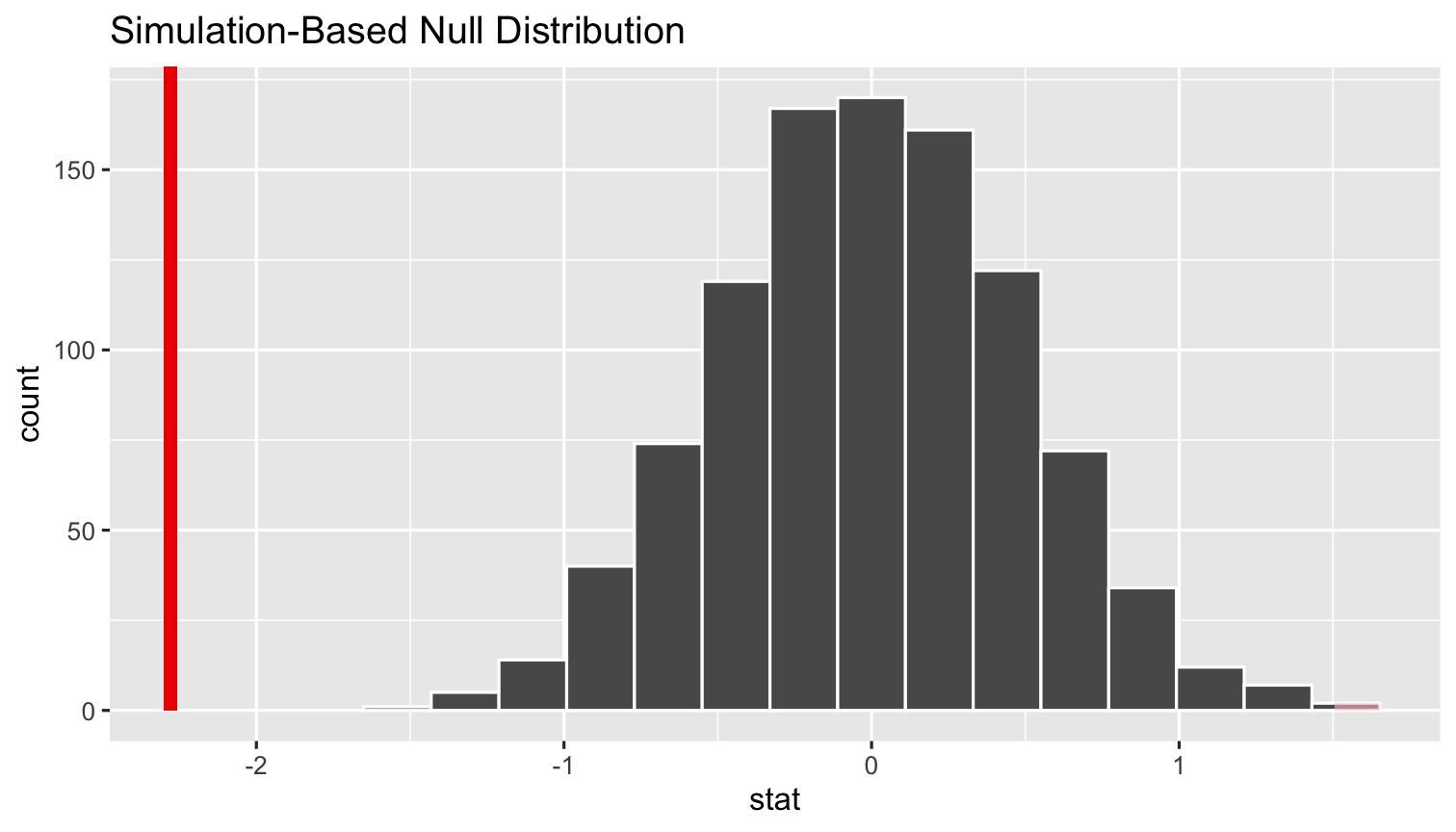
The infer Pipeline: Visualize Confidence Intervals
Specify
Hypothesize
Generate
Calculate
Visualize
%>% visualize()+ shade_ci()- To shade confidence interval, we first need a vector of what they are
- I've saved the outputted
tibbleof them from 4 slides ago asci_values
- I've saved the outputted
simulations %>% visualize(obs_stat = sample_slope)+ shade_confidence_interval(ci_values)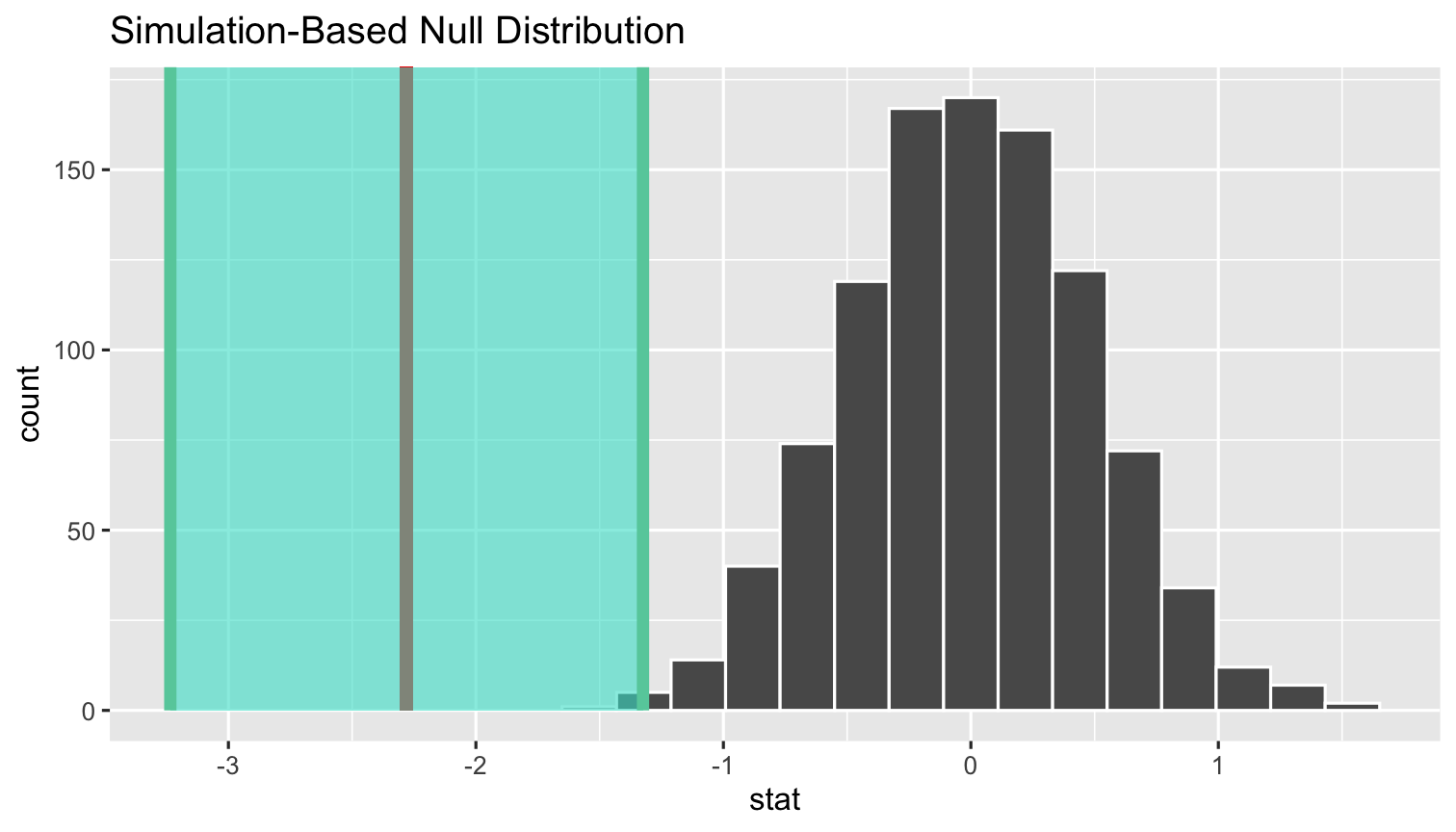
The infer Pipeline: Visualize is a Wrapper of ggplot
infer'svisualize()function is just a wrapper function forggplot()- you can take your
simulationstibbleand justggplota normal histogram
- you can take your
The infer Pipeline: Visualize is a Wrapper of ggplot
infer'svisualize()function is just a wrapper function forggplot()- you can take your
simulationstibbleand justggplota normal histogram
- you can take your
simulations %>% ggplot(data = .)+ aes(x = stat)+ geom_histogram(color="white", fill="indianred")+ geom_vline(xintercept = sample_slope, color = "blue", size = 2, linetype = "dashed")+ labs(x = expression(paste("Distribution of ", hat(beta[1]), " under ", H[0], " that ", beta[1]==0)), y = "Samples")+ theme_classic(base_family = "Fira Sans Condensed", base_size=20)The infer Pipeline: Visualize is a Wrapper of ggplot
infer'svisualize()function is just a wrapper function forggplot()- you can take your
simulationstibbleand justggplota normal histogram
- you can take your
simulations %>% ggplot(data = .)+ aes(x = stat)+ geom_histogram(color="white", fill="indianred")+ geom_vline(xintercept = sample_slope, color = "blue", size = 2, linetype = "dashed")+ labs(x = expression(paste("Distribution of ", hat(beta[1]), " under ", H[0], " that ", beta[1]==0)), y = "Samples")+ theme_classic(base_family = "Fira Sans Condensed", base_size=20)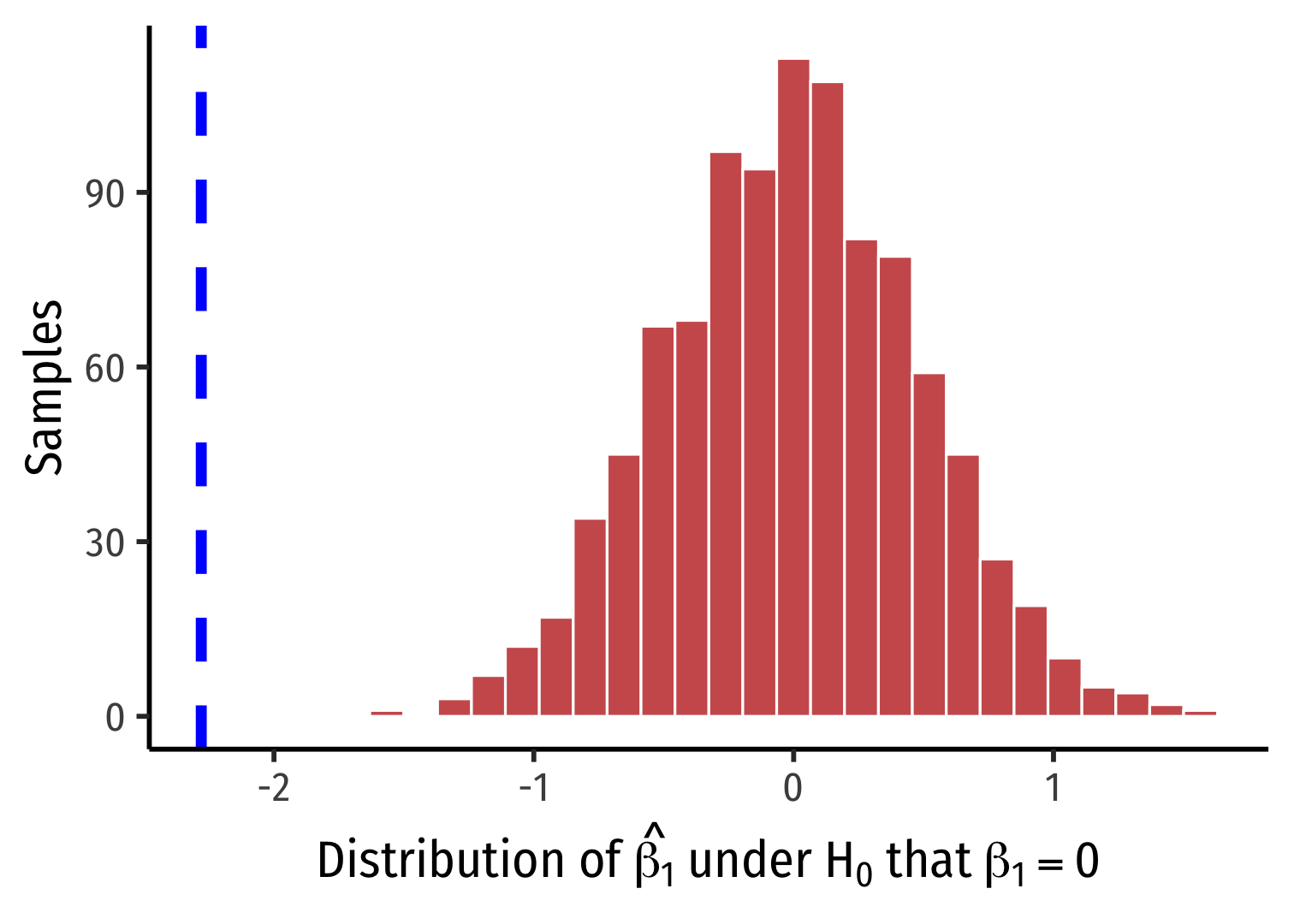
What R Does: Classical Statistical Inference I
R does things the old-fashioned way, using a theoretical null distribution instead of simulation
A t-distribution with n−k−1 df1
Calculate a t-statistic for ^β1:
test statistic=estimate−null hypothesisstandard error of estimate
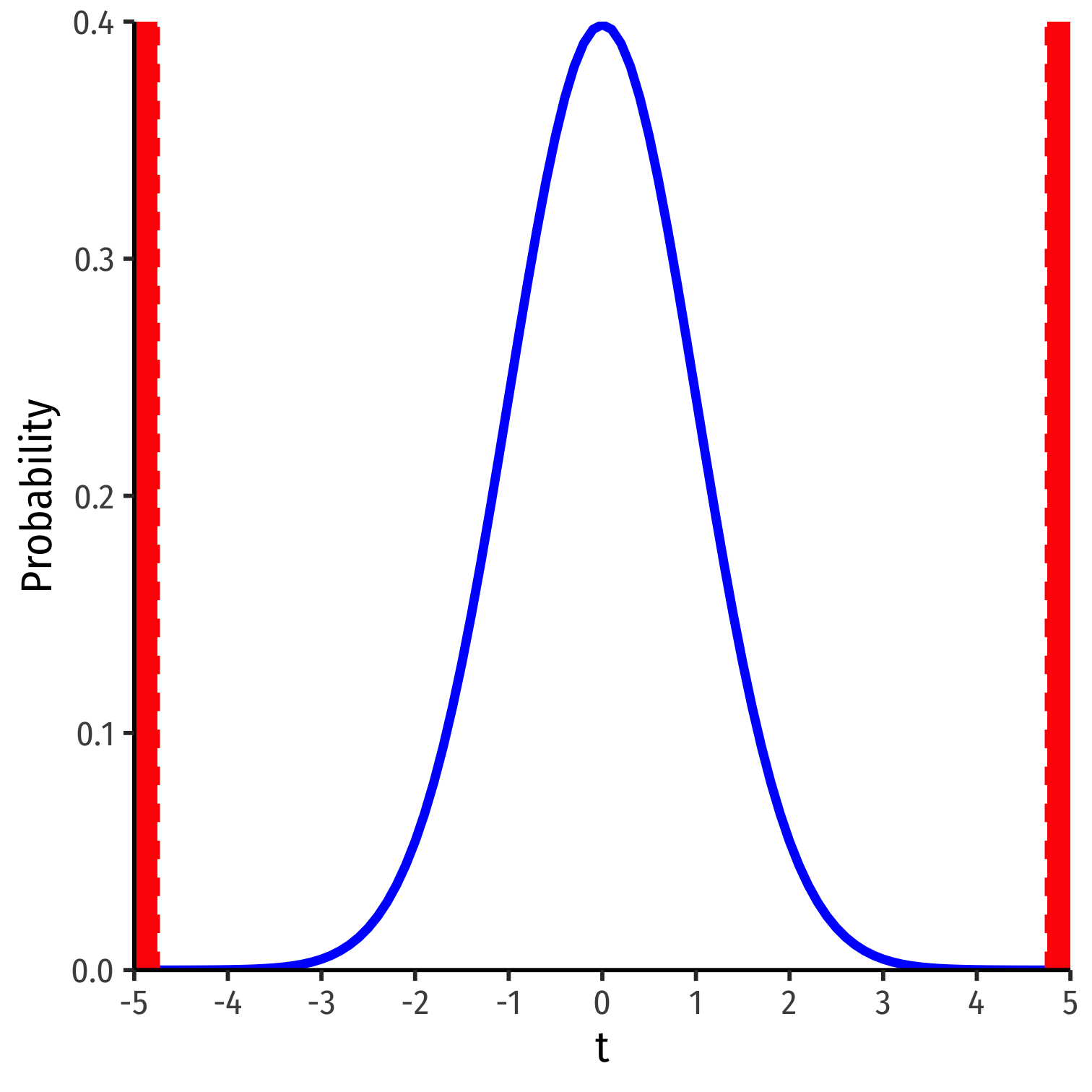
1 k is the number of X variables.
What R Does: Classical Statistical Inference II
test statistic=estimate−null hypothesisstandard error of estimate
t has the same interpretation as Z, number of std. dev. away from the distribution's center1
Compares to a critical value of t∗ (determined by α & n−k−1)
- For 95% confidence, α=0.05, t∗≈22
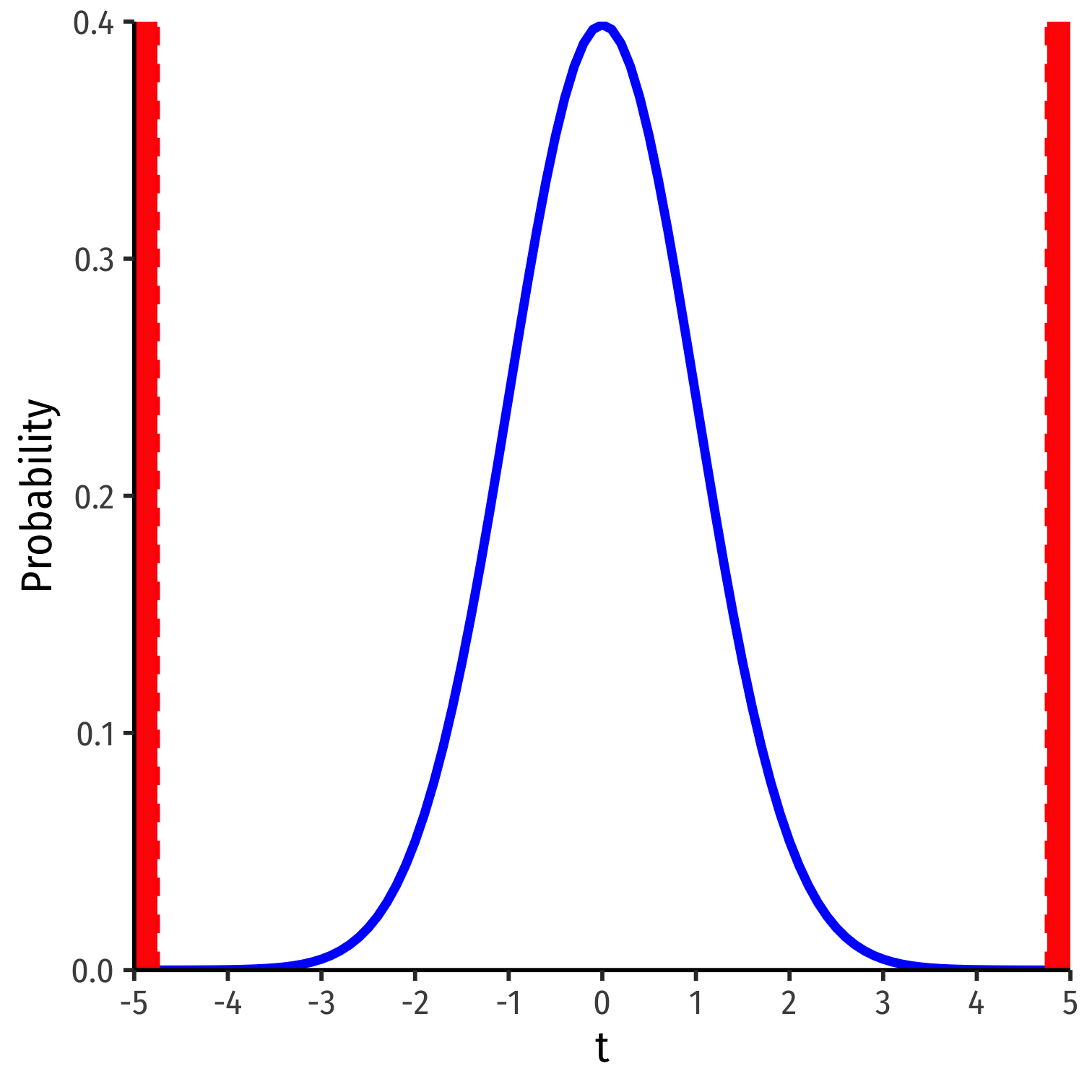
1 Think of our simulated distribution, the center was 0.
2 The 68-95-99.7% empirical rule!
What R Does: Classical Statistical Inference III
t=^β1−β1,0se(^β1)t=−2.28−00.48t=−4.75
Our sample slope is 4.75 standard deviations below the mean under H0
p-value: prob. of a test statistic at least as large (in magnitude) as ours if the null hypothesis were true1
- p-value is 2-sided for Ha:β1≠0
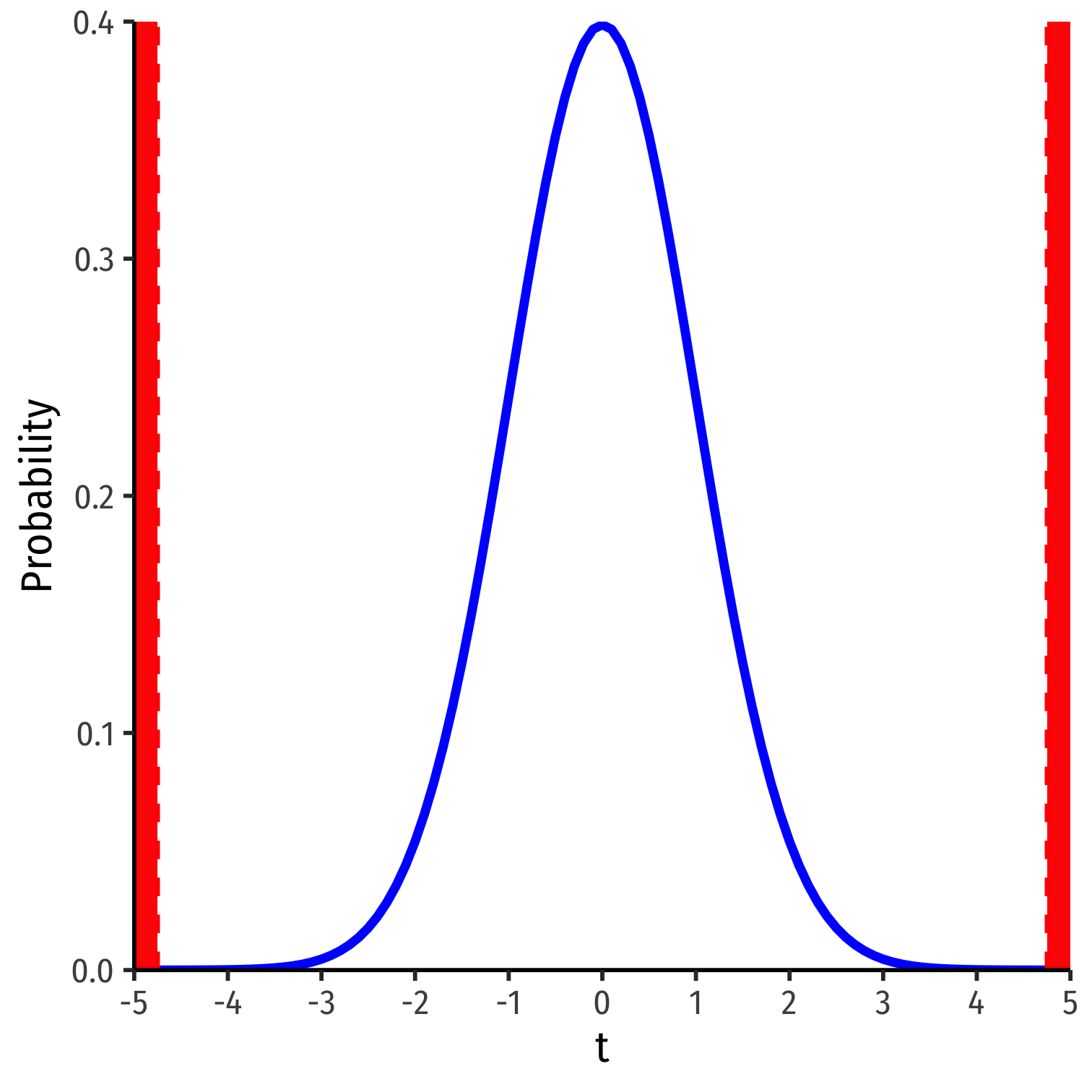
1 Think of our simulated distribution, the center was 0.
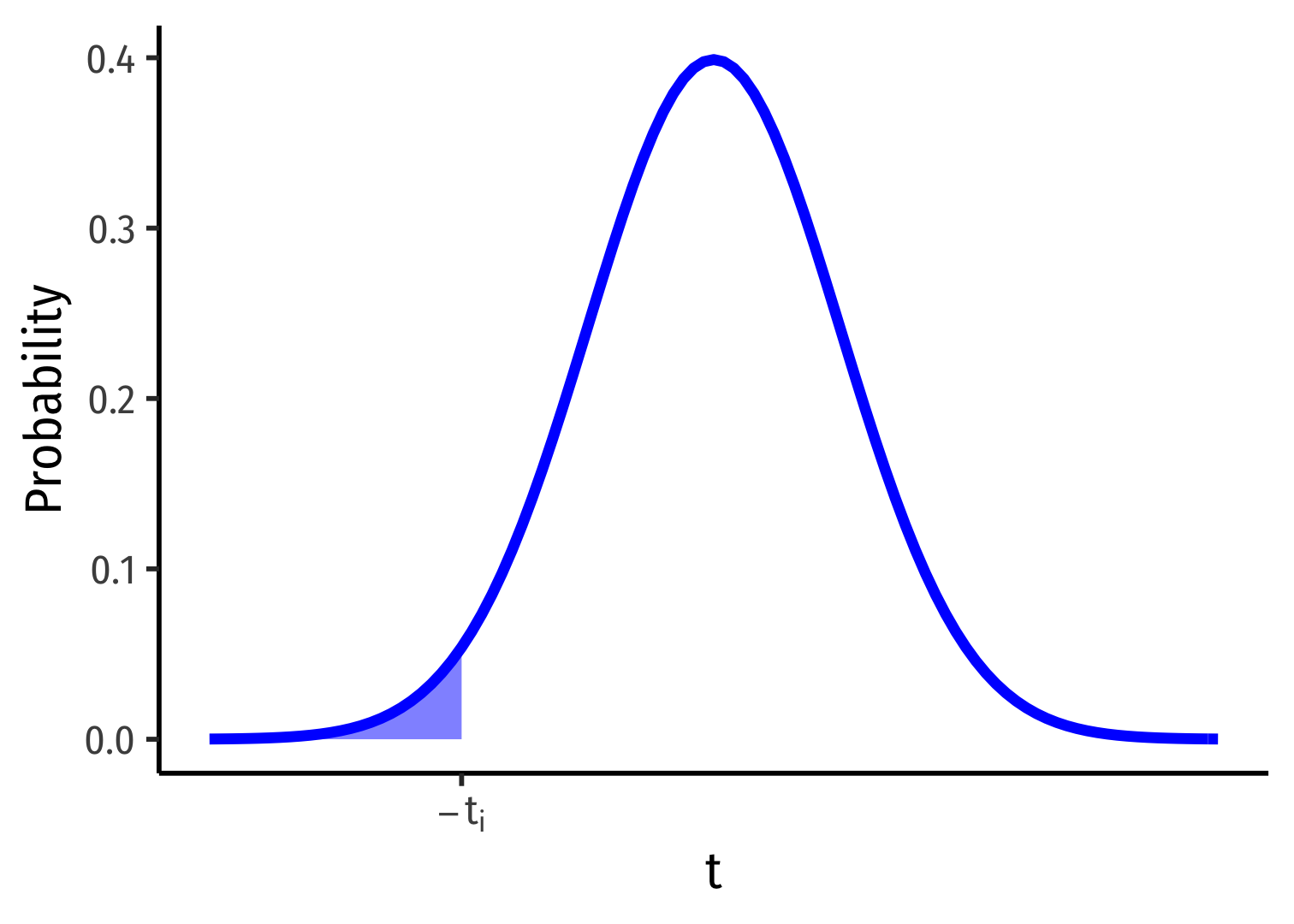
1-Sided vs. 2-Sided p-values I
Ha:β1<0
p-value: Prob(t<ti)
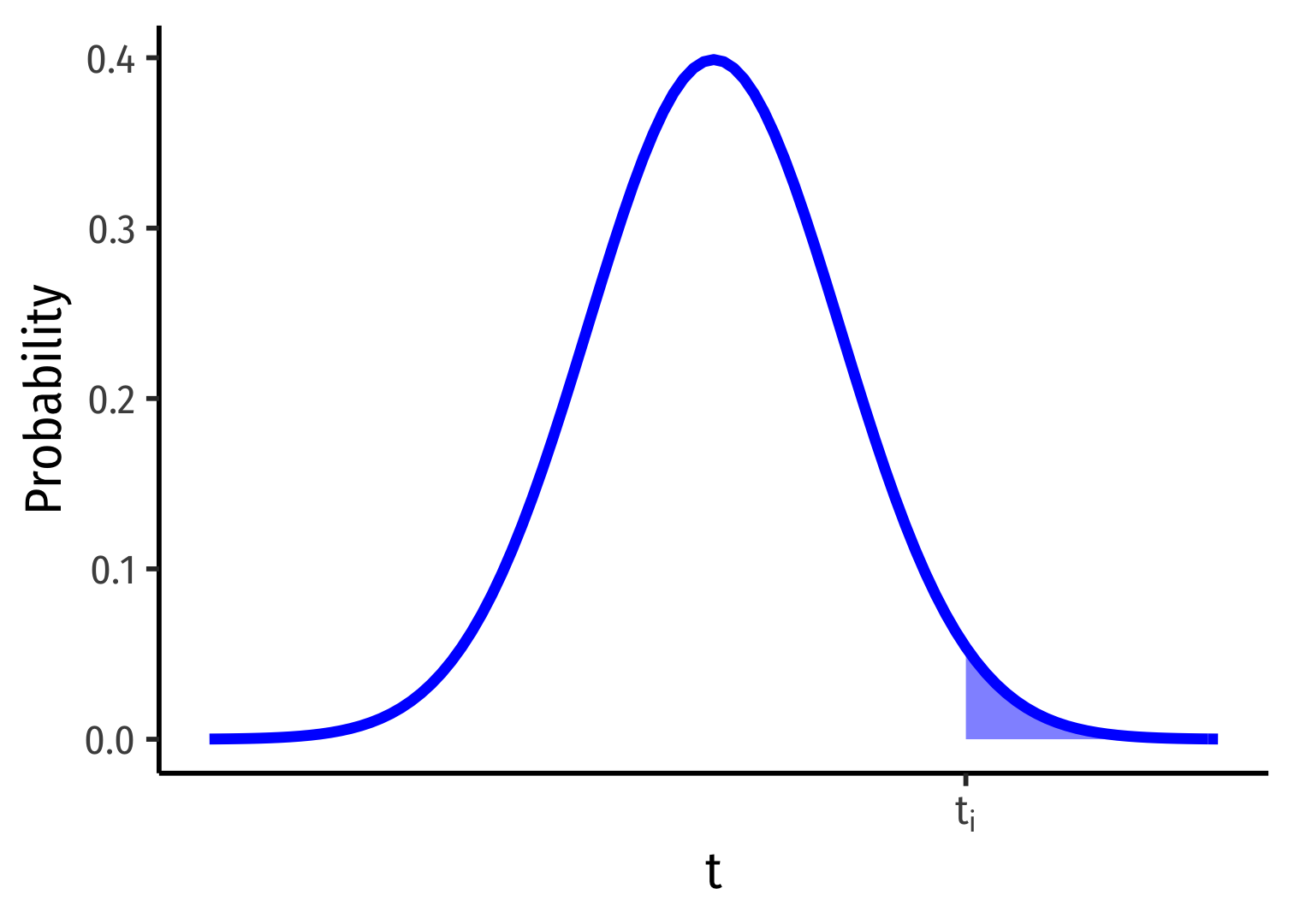
Ha:β1>0
p-value: Prob(t>ti)
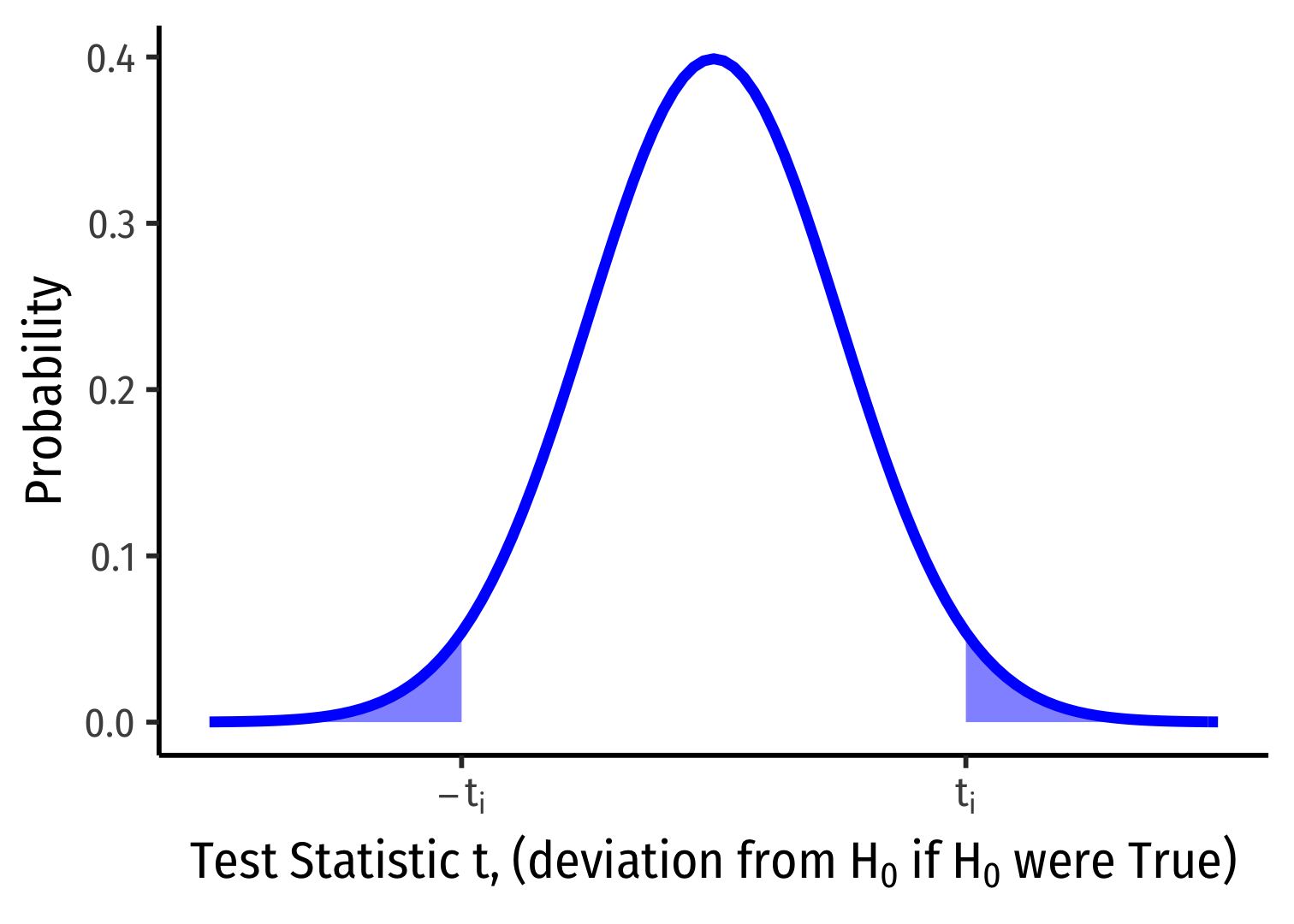
1-Sided vs. 2-Sided p-values I
Ha:β1≠0
p-value: 2×Prob(t>|ti|)
Hypothesis Tests in Regression Output I
summary(school_reg)## ## Call:## lm(formula = testscr ~ str, data = CASchool)## ## Residuals:## Min 1Q Median 3Q Max ## -47.727 -14.251 0.483 12.822 48.540 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 698.9330 9.4675 73.825 < 2e-16 ***## str -2.2798 0.4798 -4.751 2.78e-06 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 18.58 on 418 degrees of freedom## Multiple R-squared: 0.05124, Adjusted R-squared: 0.04897 ## F-statistic: 22.58 on 1 and 418 DF, p-value: 2.783e-06Hypothesis Tests in Regression Output II
- In
broom'stidy()(with confidence intervals)
tidy(school_reg, conf.int=TRUE)| ABCDEFGHIJ0123456789 |
term <chr> | estimate <dbl> | std.error <dbl> | statistic <dbl> | p.value <dbl> | conf.low <dbl> | conf.high <dbl> |
|---|---|---|---|---|---|---|
| (Intercept) | 698.932952 | 9.4674914 | 73.824514 | 6.569925e-242 | 680.32313 | 717.542779 |
| str | -2.279808 | 0.4798256 | -4.751327 | 2.783307e-06 | -3.22298 | -1.336637 |
Conclusions
H0:β1=0Ha:βa≠0
Because the hypothesis test's p-value < α (0.05)...
We have sufficient evidence to reject H0 in favor of our alternative hypothesis. Our sample suggests that there is a relationship between class size and test scores.
Conclusions
H0:β1=0Ha:βa≠0
Because the hypothesis test's p-value < α (0.05)...
We have sufficient evidence to reject H0 in favor of our alternative hypothesis. Our sample suggests that there is a relationship between class size and test scores.
Using the confidence intervals:
We are 95% confident that the true marginal effect of class size on test scores is between −3.22 and −1.34.
Hypothesis Testing and Confidence Intervals: Relationship
Confidence intervals are all two-sided by nature CI0.95=([^β1−2×se(^β1)],[^β1+2×se(^β1]))
Hypothesis test (t-test) of H0:β1=0 computes a t-value of1 t=^β1se(^β1)
and p<0.05 when t≥2
Hypothesis Testing and Confidence Intervals: Relationship
Confidence intervals are all two-sided by nature CI0.95=([^β1−2×se(^β1)],[^β1+2×se(^β1]))
Hypothesis test (t-test) of H0:β1=0 computes a t-value of1 t=^β1se(^β1)
and p<0.05 when t≥2If a confidence interval contains the H0 value (i.e. 0, for our test), then we fail to reject H0.
1 Since our null hypothesis is that (\beta_{1,0}=0), the test statistic simplifies to this neat fraction.
Common Misconceptions about p-values
- All of the following are FALSE interpretations of p (and below are reasons why each is wrong)
- p is the probability that the alternative hypothesis is false
- We can never prove an alternative hypothesis, only tentatively reject a null hypothesis
Common Misconceptions about p-values
- All of the following are FALSE interpretations of p (and below are reasons why each is wrong)
p is the probability that the alternative hypothesis is false
- We can never prove an alternative hypothesis, only tentatively reject a null hypothesis
p is the probability that the null hypothesis is true
- We're not proving the H0 is false, only saying that it's very unlikely that if H0 were true, we'd obtain a slope as rare as our sample's slope
Common Misconceptions about p-values
- All of the following are FALSE interpretations of p (and below are reasons why each is wrong)
p is the probability that the alternative hypothesis is false
- We can never prove an alternative hypothesis, only tentatively reject a null hypothesis
p is the probability that the null hypothesis is true
- We're not proving the H0 is false, only saying that it's very unlikely that if H0 were true, we'd obtain a slope as rare as our sample's slope
p is the probability that our observed effects were produced purely by random chance
- p is computed under a specific model (think about our null world) that assumes H0 is true
Common Misconceptions about p-values
- All of the following are FALSE interpretations of p (and below are reasons why each is wrong)
p is the probability that the alternative hypothesis is false
- We can never prove an alternative hypothesis, only tentatively reject a null hypothesis
p is the probability that the null hypothesis is true
- We're not proving the H0 is false, only saying that it's very unlikely that if H0 were true, we'd obtain a slope as rare as our sample's slope
p is the probability that our observed effects were produced purely by random chance
- p is computed under a specific model (think about our null world) that assumes H0 is true
p tells us how significant our finding is
- p tells us nothing about the size or the real world significance of any effect deemed "statistically significant"
- it only tells us that the slope is statistically significantly different from 0 (if H0 is β1=0)
Abusing p-Values I

Abusing p-Values II

"The widespread use of 'statistical significance' (generally interpreted as (p≤0.05) as a license for making a claim of a scientific finding (or implied truth) leads to considerable distortion of the scientific process."
Wasserstein, Ronald L. and Nicole A. Lazar, (2016), "The ASA's Statement on p-Values: Context, Process, and Purpose," The American Statistician 30(2): 129-133
p-value Clarification
Again, p-value is the probability that, assuming the null hypothesis is true, we obtain (by pure random chance) a test statistic at least as extreme as the one we estimated for our sample
A low p-value means either (and we can't distinguish which):
- H0 is true and a highly improbable event has occurred OR
- H0 is false
Significance In Regression Tables
| Test Score | |
| Intercept | 698.93 *** |
| (9.47) | |
| STR | -2.28 *** |
| (0.48) | |
| N | 420 |
| R-Squared | 0.05 |
| SER | 18.58 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |
Statistical significance is shown by asterisks, common (but not always!) standard:
- 1 asterisk: significant at α=0.10
- 2 asterisks: significant at α=0.05
- 3 asterisks: significant at α=0.01
Rare, but sometimes regression tables include p-values for estimates

