+ - 0:00:00
Notes for current slide
Notes for next slide

2.5: OLS: Precision and Diagnostics

ECON 480 · Econometrics · Fall 2019

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsf19
metricsF19.classes.ryansafner.com

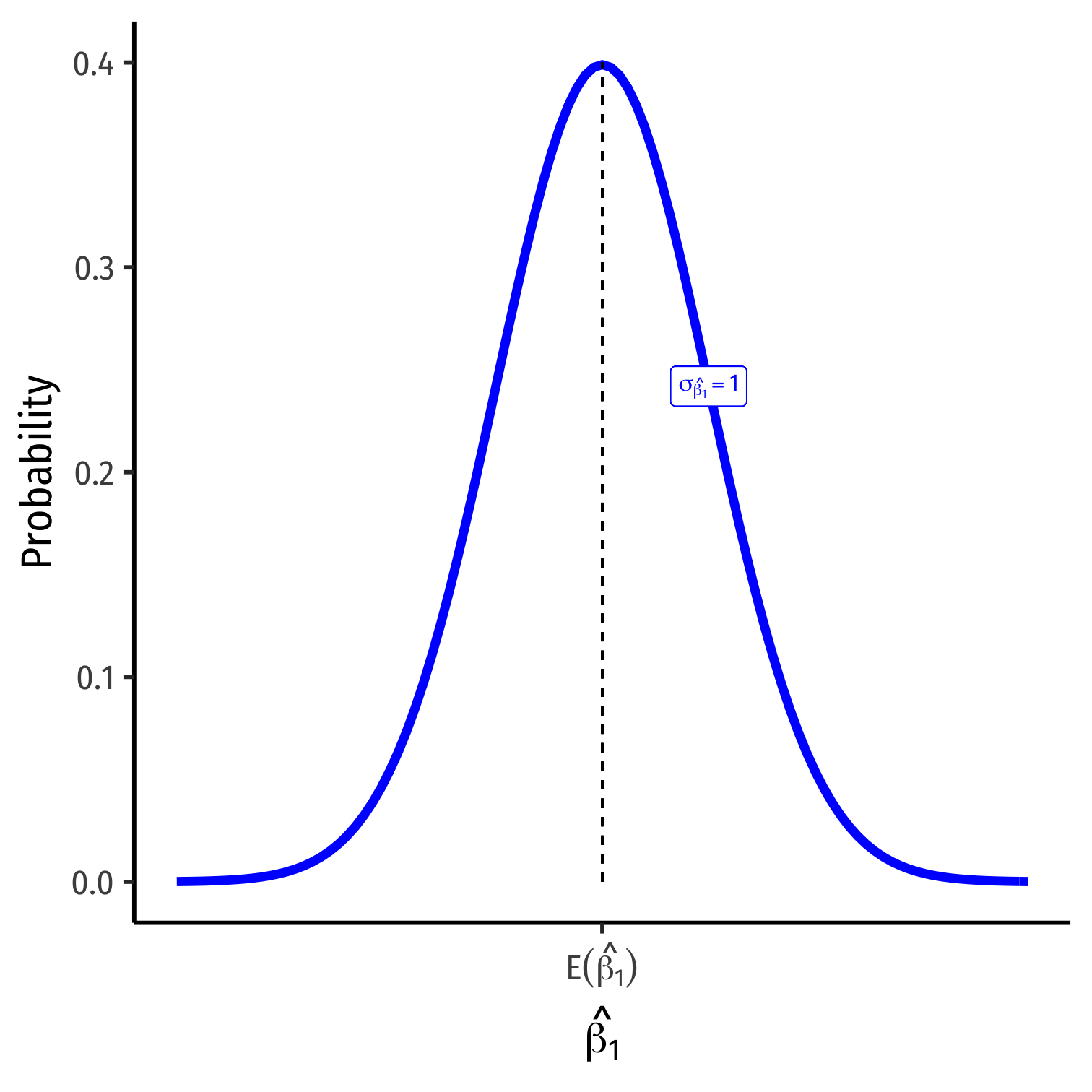
The Sampling Distribution of ^β1

^β1∼N(E[^β1],σ^β1)

  1. E[^β1]; the center of the distribution (last class)
    • E[^β1]=β11

The Sampling Distribution of ^β1

^β1∼N(E[^β1],σ^β1)

  1. E[^β1]; the center of the distribution (last class)

    • E[^β1]=β11

  2. σ^β1; how precise is our estimate? (today)

    • Variance σ2^β1 or standard error+ σ^β1

1 Under the 4 assumptions about u (particularly, cor(X,u)=0).

+ Standard "error" is the analog of standard deviation when talking about
the sampling distribution of a sample statistic (such as ˉX or ^β1).

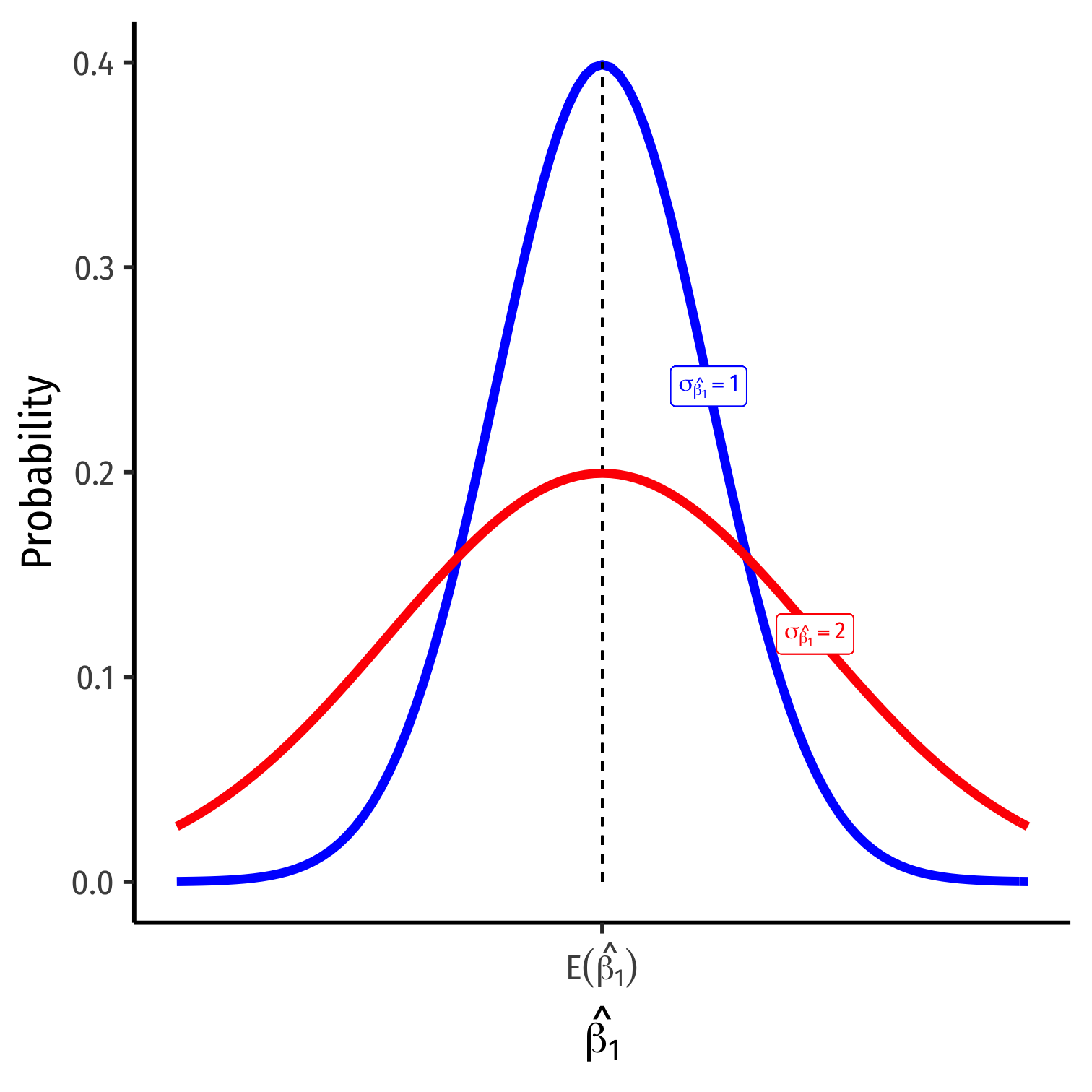
Variation in ^β1

What Affects Variation in ^β1

var(^β1)=(SER)2n×var(X)

se(^β1)=√var(^β1)=SER√n×sd(X)

  • Variation in ^β1 is affected by three things:
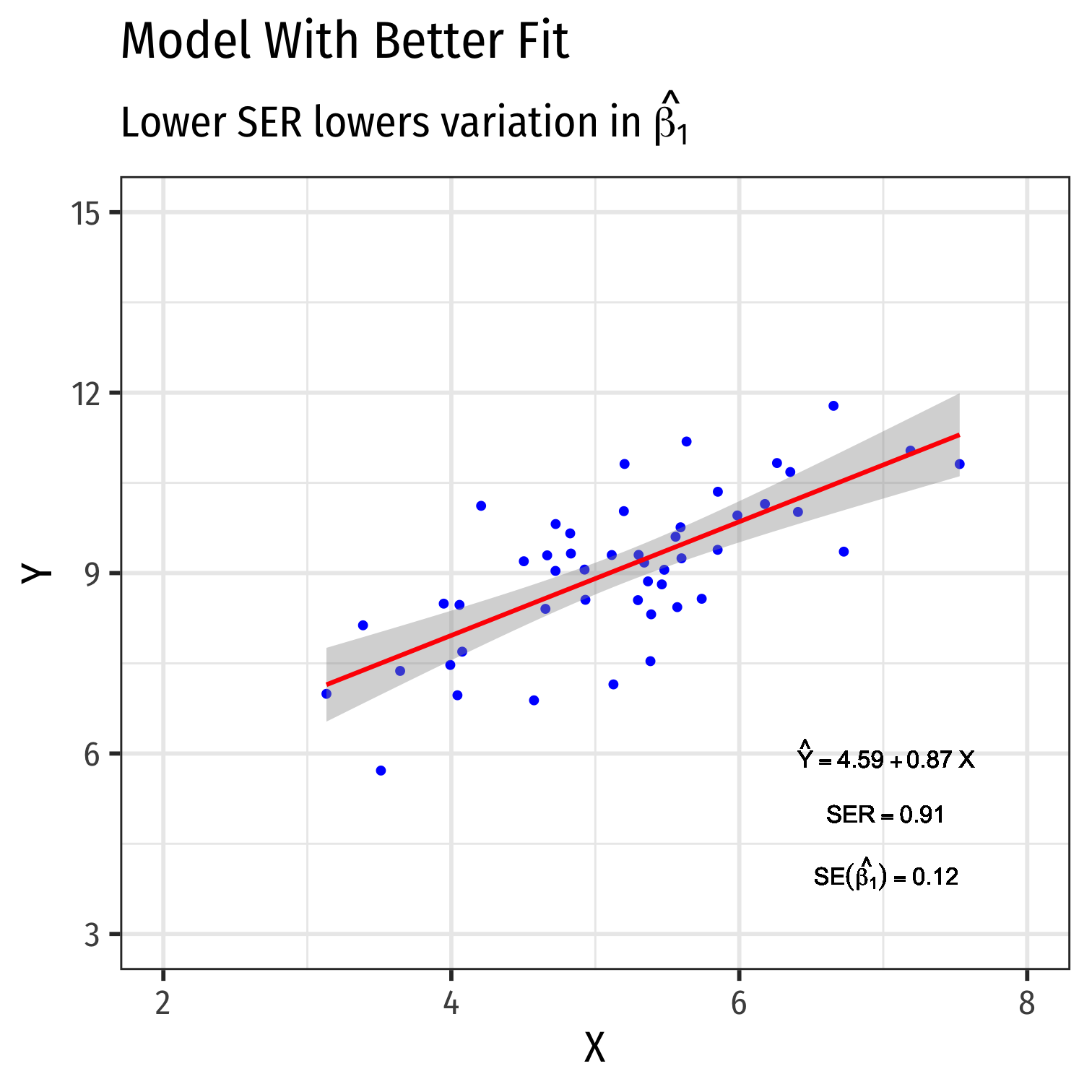
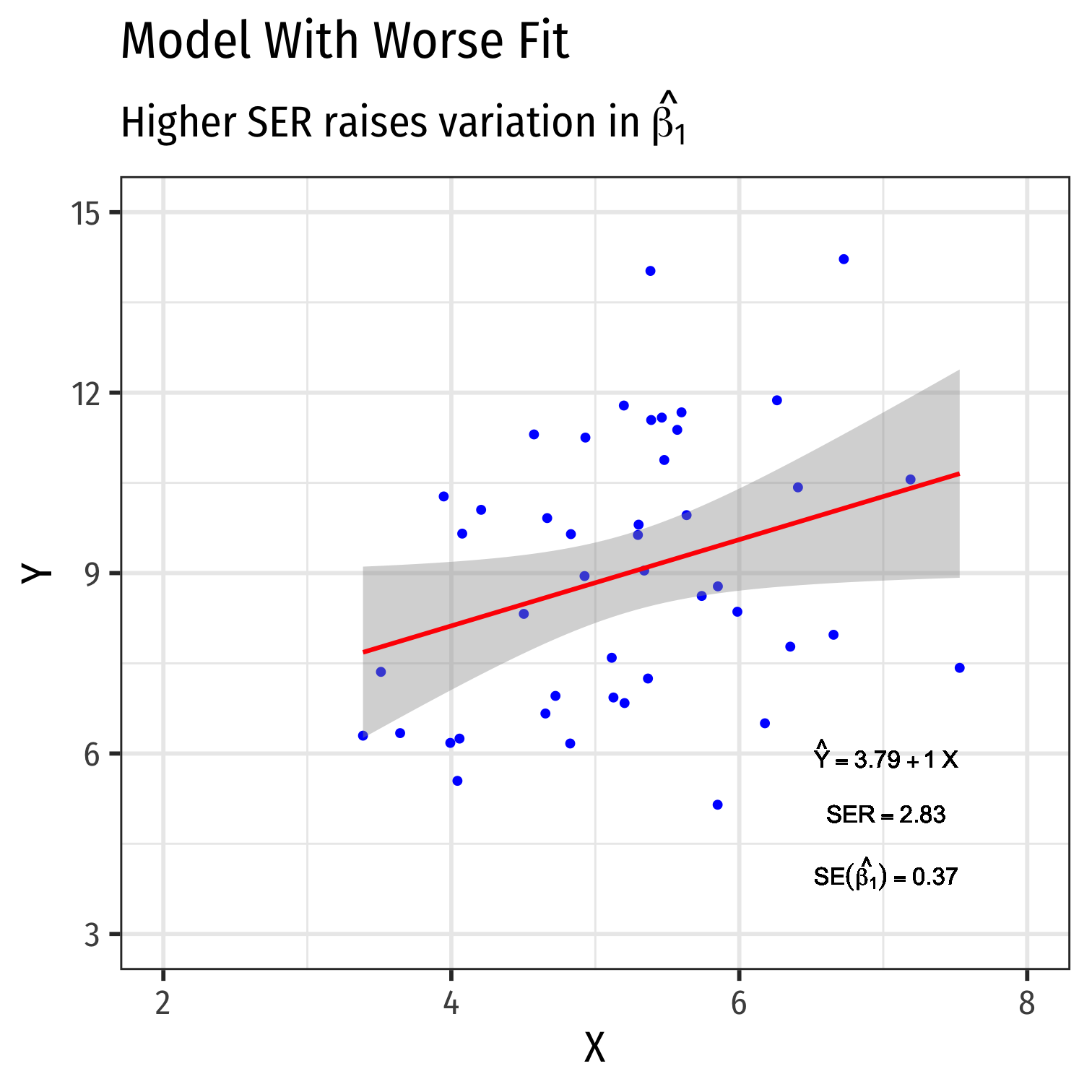
  1. Goodness of fit of the model (SER)+
    • Larger SER → larger var(^β1)
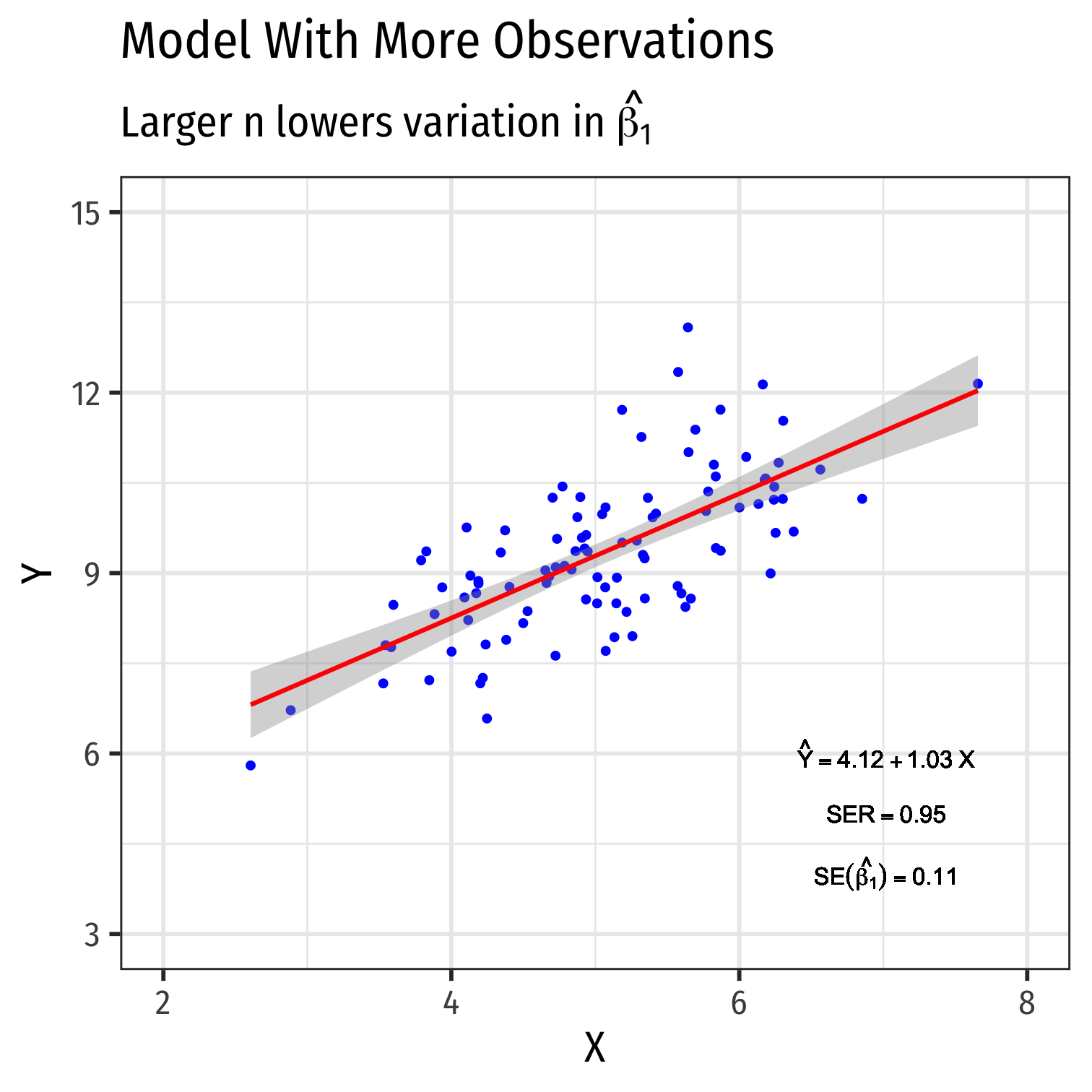
  2. Sample size, n
    • Larger n → smaller var(^β1)
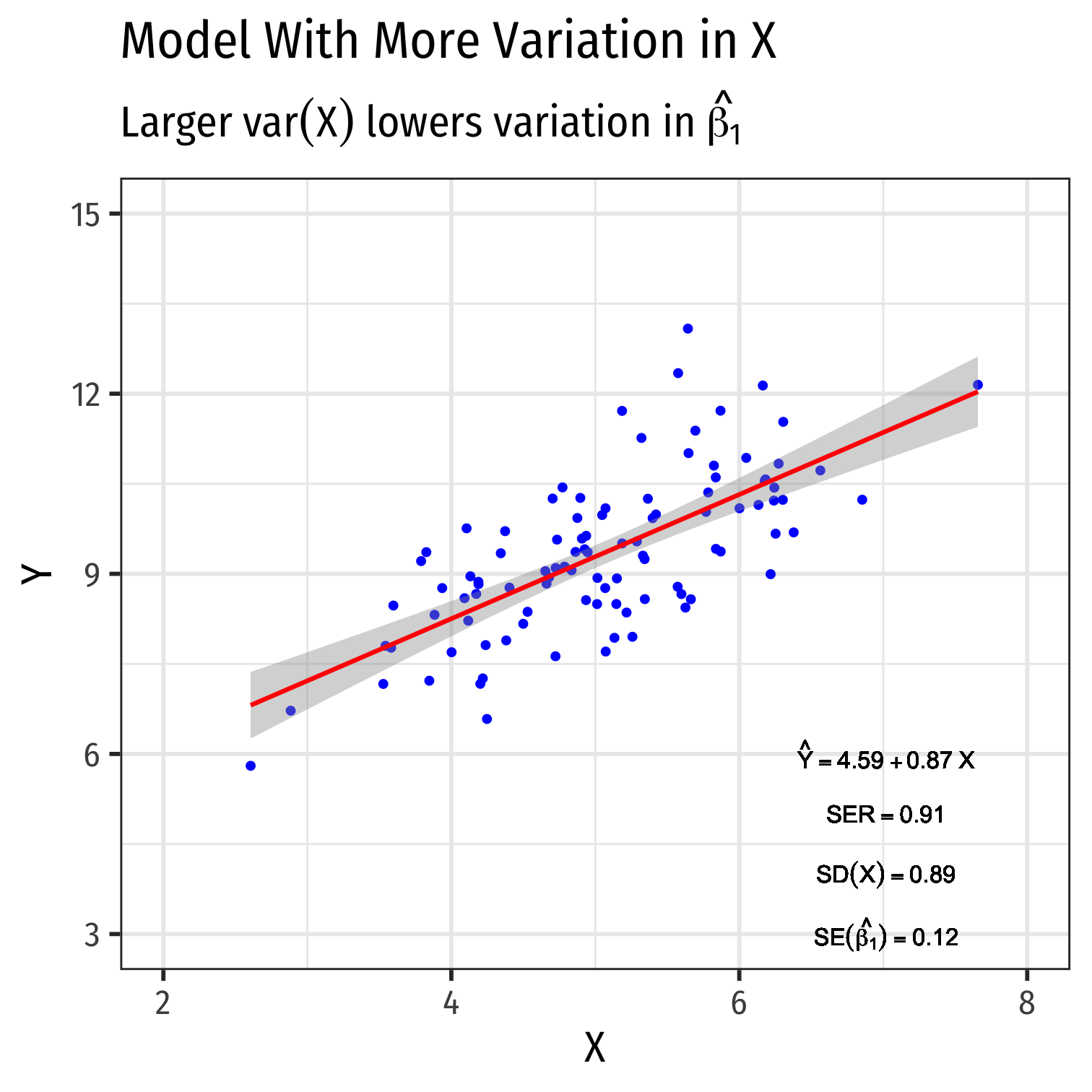
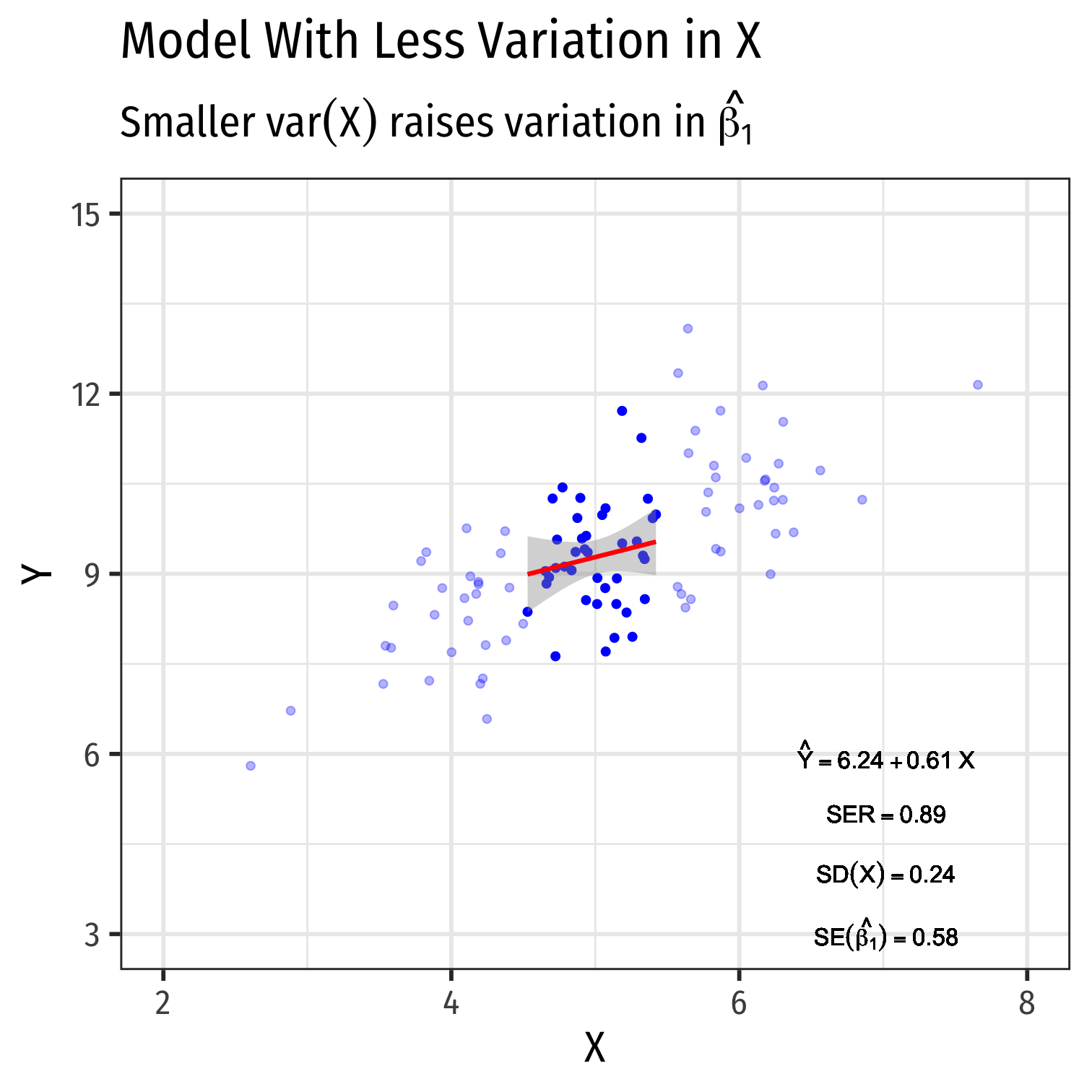
  3. Variance of X
    • Larger var(X) → smaller var(^β1)

+ Recall from last class, the Standard Error of the Regression ^σu=√∑^ui2n−2

Variation in ^β1: Goodness of Fit

Variation in ^β1: Sample Size

Variation in ^β1: Variation in X

Presenting Regression Results

Our Class Size Regression: Base R

summary(school_reg) # get full summary
## 
## Call:
## lm(formula = testscr ~ str, data = CASchool)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -47.727 -14.251   0.483  12.822  48.540 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 698.9330     9.4675  73.825  < 2e-16 ***
## str          -2.2798     0.4798  -4.751 2.78e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 18.58 on 418 degrees of freedom
## Multiple R-squared:  0.05124,    Adjusted R-squared:  0.04897 
## F-statistic: 22.58 on 1 and 418 DF,  p-value: 2.783e-06
  • How can we present all of this information in a tidy way?

Our Class Size Regression: Broom I

  • broom's tidy() gives us a little bit neater table
library(broom)
tidy(school_reg)
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
p.value
<dbl>
(Intercept)698.9329529.467491473.8245146.569925e-242
str-2.2798080.4798256-4.7513272.783307e-06
2 rows

Our Class Size Regression: Broom II

  • broom's glance() gives us summary statistics about the regression
library(broom)
glance(school_reg)
ABCDEFGHIJ0123456789
r.squared
<dbl>
adj.r.squared
<dbl>
sigma
<dbl>
statistic
<dbl>
p.value
<dbl>
df
<int>
logLik
<dbl>
AIC
<dbl>
BIC
<dbl>
0.05124010.0489703318.5809722.575112.783307e-062-1822.253650.4993662.62
1 row | 1-9 of 11 columns

Presenting Regressions in a Table

  • Professional journals and papers often have a regression table, including:

    • Estimates of ^β0 and ^β1
    • Standard errors of ^β0 and ^β1 (often below, in parentheses)
    • Indications of statistical significance (often with asterisks)
    • Measures of regression fit: R2, SER, etc

  • Later: multiple columns for multiple models

Test Score
Intercept 698.93 ***
(9.47)   
STR -2.28 ***
(0.48)   
N 420       
R-Squared 0.05    
SER 18.58    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Regression Output with huxtable I

  • You will need to first install.packages("huxtable")

  • Load with library(huxtable)

  • Command: huxreg()

  • Main argument is the name of your lm object

  • Default output is fine, but often we want to customize a bit

# install.packages("huxtable")
library(huxtable)
huxreg(school_reg)
(1)
(Intercept) 698.933 ***
(9.467)   
str -2.280 ***
(0.480)   
N 420        
R2 0.051    
logLik -1822.250    
AIC 3650.499    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Regression Output with huxtable II

  • Can give title to each column
"Test Score" = school_reg

Regression Output with huxtable II

  • Can give title to each column
"Test Score" = school_reg
  • Can change name of coefficients from default
coefs = c("Intercept" = "(Intercept)",
          "STR" = "str")

Regression Output with huxtable II

  • Can give title to each column
"Test Score" = school_reg
  • Can change name of coefficients from default
coefs = c("Intercept" = "(Intercept)",
          "STR" = "str")
  • Decide what statistics to include, and rename them
statistics = c("N" = "nobs",
               "R-Squared" = "r.squared",
               "SER" = "sigma")

Regression Output with huxtable II

  • Can give title to each column
"Test Score" = school_reg
  • Can change name of coefficients from default
coefs = c("Intercept" = "(Intercept)",
          "STR" = "str")
  • Decide what statistics to include, and rename them
statistics = c("N" = "nobs",
               "R-Squared" = "r.squared",
               "SER" = "sigma")
  • Choose how many decimal places to round to
number_format = 2

Regression Output with huxtable III

huxreg("Test Score" = school_reg,
       coefs = c("Intercept" = "(Intercept)",
                 "STR" = "str"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 2)

Regression Output with huxtable III

huxreg("Test Score" = school_reg,
       coefs = c("Intercept" = "(Intercept)",
                 "STR" = "str"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 2)
Test Score
Intercept 698.93 ***
(9.47)   
STR -2.28 ***
(0.48)   
N 420       
R-Squared 0.05    
SER 18.58    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Regression Outputs

  • huxtable is one package you can use

  • I used to only use stargazer, but as it was originally meant for STATA, it has limits and problems

Diagnostics about Regression

Diagnostics: Residuals I

  • We often look at the residuals of a regression to get more insight about its goodness of fit and its bias

  • Recall broom's augment creates some useful new variables

    • .fitted are fitted (predicted) values from model, i.e. ˆYi
    • .resid are residuals (errors) from model, i.e. ˆui

Diagnostics: Residuals II

  • Often a good idea to store in a new object (so we can make some plots)
aug_reg<-augment(school_reg)
aug_reg %>%
  head()
testscr str .fitted .se.fit .resid .hat .sigma .cooksd .std.resid
691 17.9 658 1.24 32.7 0.00442 18.5 0.00689  1.76 
661 21.5 650 1.28 11.3 0.00475 18.6 0.000893 0.612
644 18.7 656 1.01 -12.7 0.00297 18.6 0.0007   -0.685
648 17.4 659 1.42 -11.7 0.00586 18.6 0.00117  -0.629
641 18.7 656 1.02 -15.5 0.00301 18.6 0.00105  -0.836
606 21.4 650 1.24 -44.6 0.00446 18.5 0.013    -2.4   
aug_reg<-augment(school_reg)
aug_reg %>% head()
testscr str .fitted .se.fit .resid .hat .sigma .cooksd .std.resid
691 17.9 658 1.24 32.7 0.00442 18.5 0.00689  1.76 
661 21.5 650 1.28 11.3 0.00475 18.6 0.000893 0.612
644 18.7 656 1.01 -12.7 0.00297 18.6 0.0007   -0.685
648 17.4 659 1.42 -11.7 0.00586 18.6 0.00117  -0.629
641 18.7 656 1.02 -15.5 0.00301 18.6 0.00105  -0.836
606 21.4 650 1.24 -44.6 0.00446 18.5 0.013    -2.4  

Recap: Assumptions about Errors

  • Recall the 4 critical assumptions about u:

  1. The expected value of the residuals is 0 E[u]=0

  2. The variance of the residuals over X is constant, written: var(u|X)=σ2u

  3. Errors are not correlated across observations: cor(ui,uj)=0∀i≠j

  4. No correlation between X and the error term: cor(X,u)=0 or E[u|X]=0

Assumptions 1 and 2: Errors are i.i.d.

  • Assumptions 1 and 2 assume that errors are coming from the same (normal) distribution u∼N(0,σu)

    • Assumption 1: E[u]=0
    • Assumption 2: sd(u|X)=σu
      • virtually always unknown...

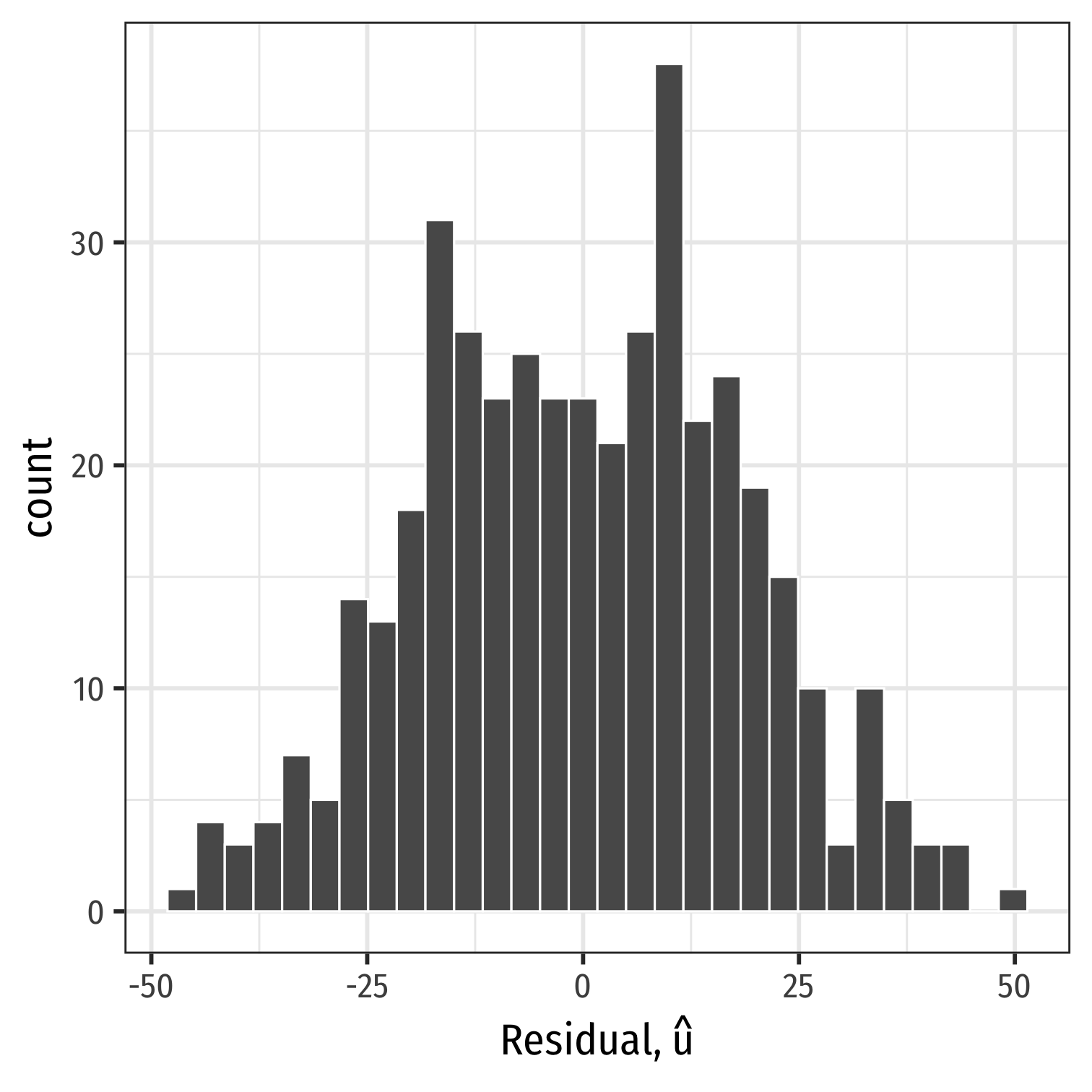
  • We often can visually check by plotting a histogram of u

Plotting Residuals

ggplot(data = aug_reg)+
  aes(x = .resid)+
  geom_histogram(color="white")+
  labs(x = expression(paste("Residual, ", hat(u))))+
  theme_bw(base_family = "Fira Sans Condensed",
           base_size=20)

Plotting Residuals

ggplot(data = aug_reg)+
  aes(x = .resid)+
  geom_histogram(color="white")+
  labs(x = expression(paste("Residual, ", hat(u))))+
  theme_bw(base_family = "Fira Sans Condensed",
           base_size=20)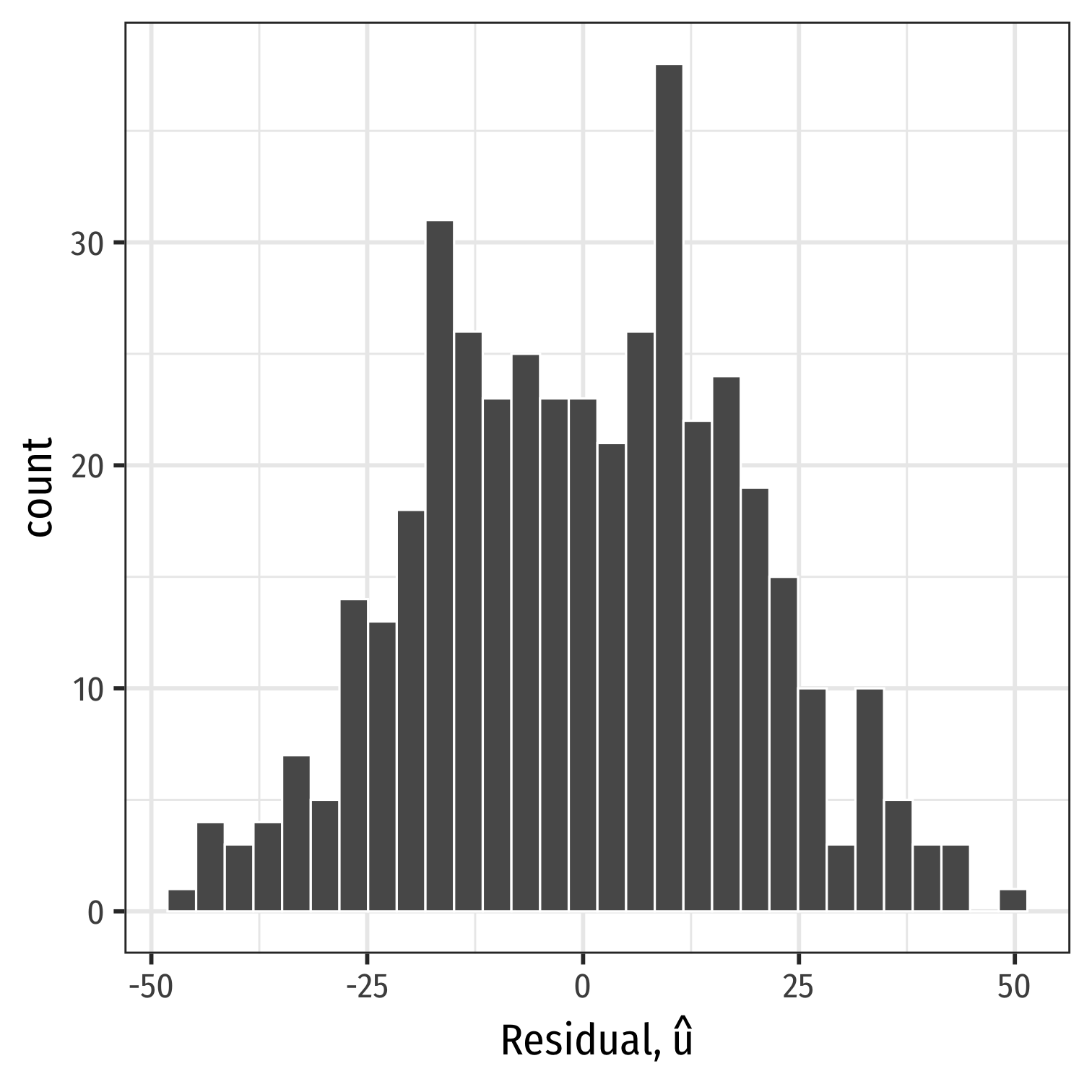

Plotting Residuals

ggplot(data = aug_reg)+
  aes(x = .resid)+
  geom_histogram(color="white")+
  labs(x = expression(paste("Residual, ", hat(u))))+
  theme_bw(base_family = "Fira Sans Condensed",
           base_size=20)
  • Just to check:
aug_reg %>%
  summarize(E_u = mean(.resid),
            sd_u = sd(.resid))
E_u sd_u
-5.76e-16 18.6

Residual Plot

  • We often plot a residual plot to see any odd patterns about residuals
    • x-axis are X values (str)
    • y-axis are u values (.resid)

Residual Plot

  • We often plot a residual plot to see any odd patterns about residuals
    • x-axis are X values (str)
    • y-axis are u values (.resid)

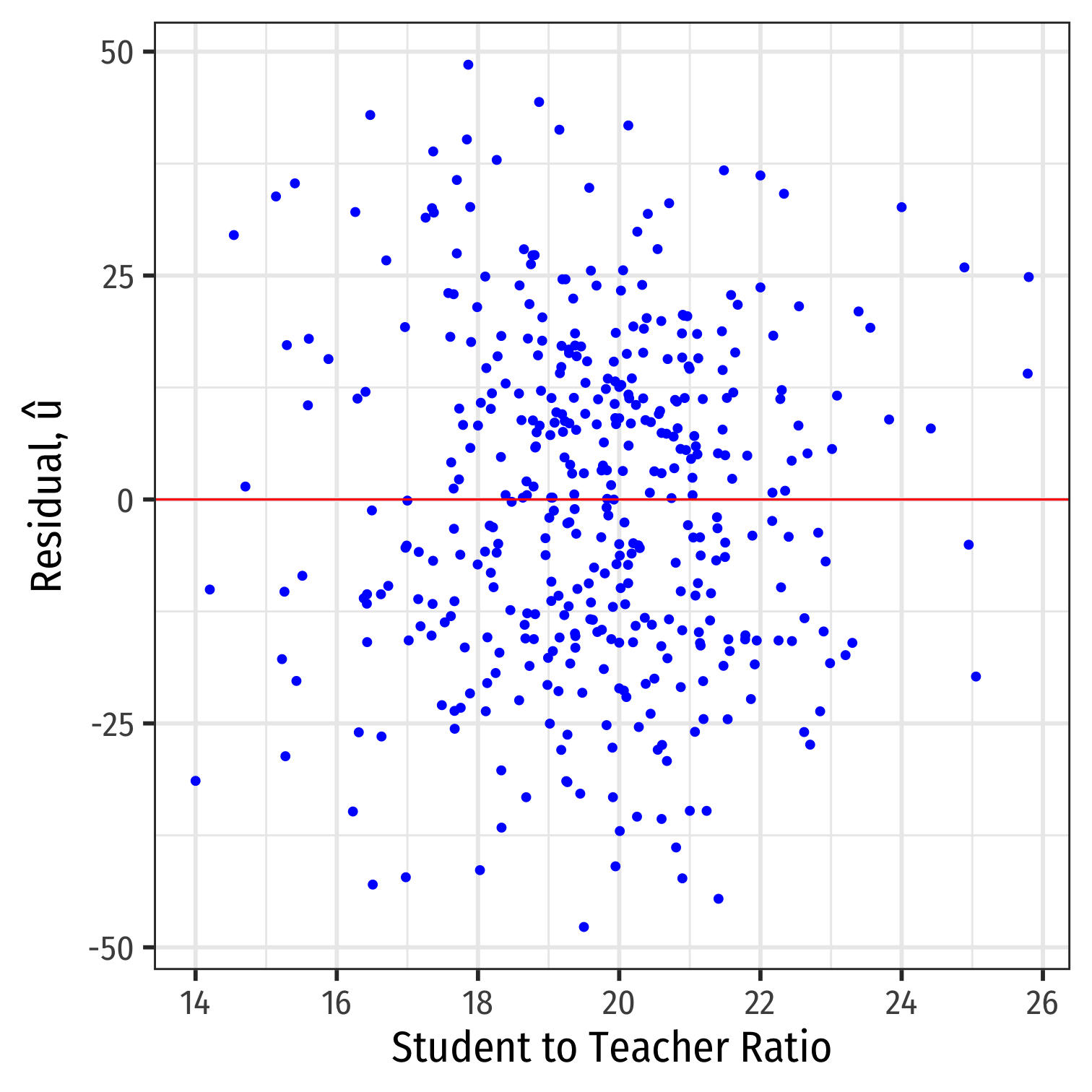
Problem: Heteroskedasticity

Homoskedasticity

  • "Homoskedasticity:" variance of the residuals over X is constant, written: var(u|X)=σ2u

  • Knowing the value of X does not affect the variance (spread) of the errors

Heteroskedasticity I

  • "Heteroskedasticity:" variance of the residuals over X is NOT constant: var(u|X)≠σ2u

  • This does not cause ^β1 to be biased, but it does cause the standard error of ^β1 to be incorrect

  • This does cause a problem for inference!

Heteroskedasticity II

  • Recall the formula for the standard error of ^β1:

se(^β1)=√var(^β1)=SER√n×sd(X)

  • This actually assumes homoskedasticity

Heteroskedasticity III

  • Under heteroskedasticity, the standard error of ^β1 mutates to:

se(^β1)=√n∑i=1(Xi−ˉX)2ˆu2[n∑i=1(Xi−ˉX)2]2

  • This is a heteroskedasticity-robust (or just "robust") method of calculating se(^β1)

  • Don't learn formula, do learn what heteroskedasticity is and how it affects our model!

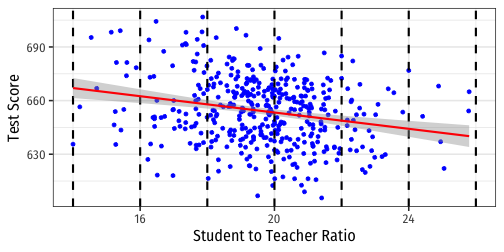
Visualizing Heteroskedasticity I

  • Our original scatterplot with regression line

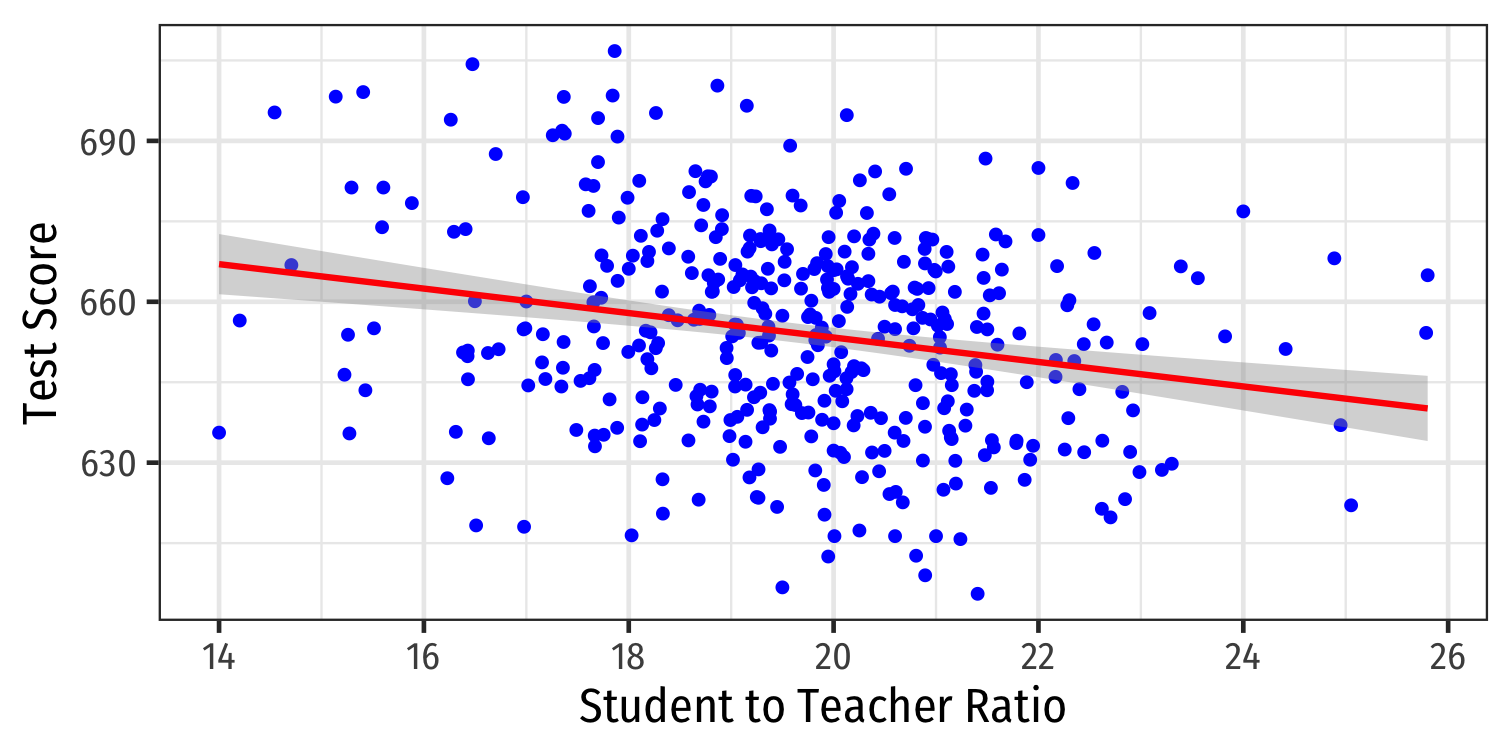
Visualizing Heteroskedasticity I

  • Our original scatterplot with regression line

  • Does the spread of the errors change over different values of str?

    • No: homoskedastic
    • Yes: heteroskedastic

Visualizing Heteroskedasticity I

  • Our original scatterplot with regression line

  • Does the spread of the errors change over different values of str?

    • No: homoskedastic
    • Yes: heteroskedastic

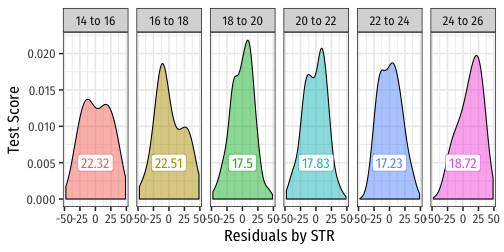
More Obvious Heteroskedasticity

  • Visual cue: data is "fan-shaped"
    • Data points are closer to line in some areas
    • Data points are more spread from line in other areas

More Obvious Heteroskedasticity

  • Visual cue: data is "fan-shaped"
    • Data points are closer to line in some areas
    • Data points are more spread from line in other areas

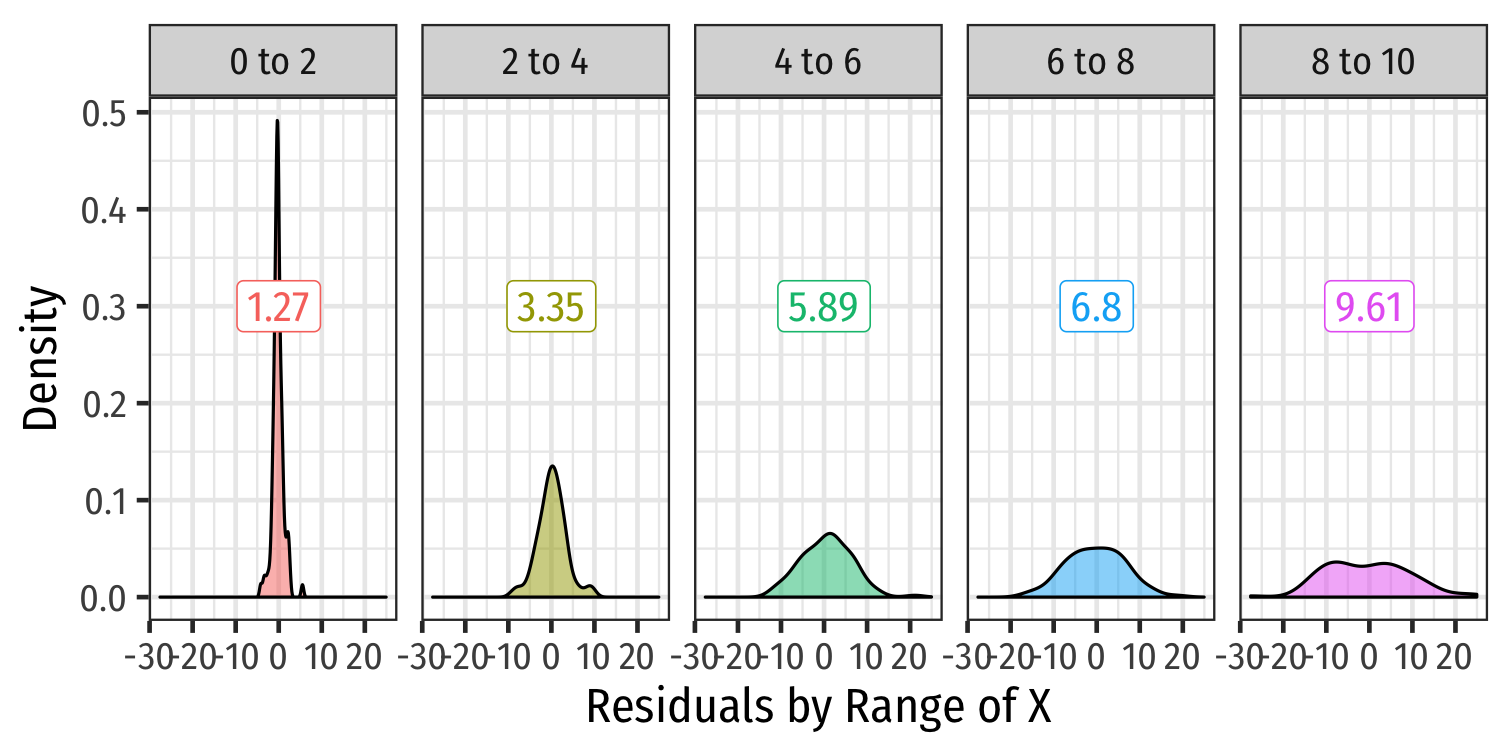
What Might Cause Heteroskedastic Errors?

^wagei=^β0+^β1educi

Wage
Intercept -0.90    
(0.68)   
Years of Schooling 0.54 ***
(0.05)   
N 526       
R-Squared 0.16    
SER 3.38    
*** p < 0.001; ** p < 0.01; * p < 0.05.

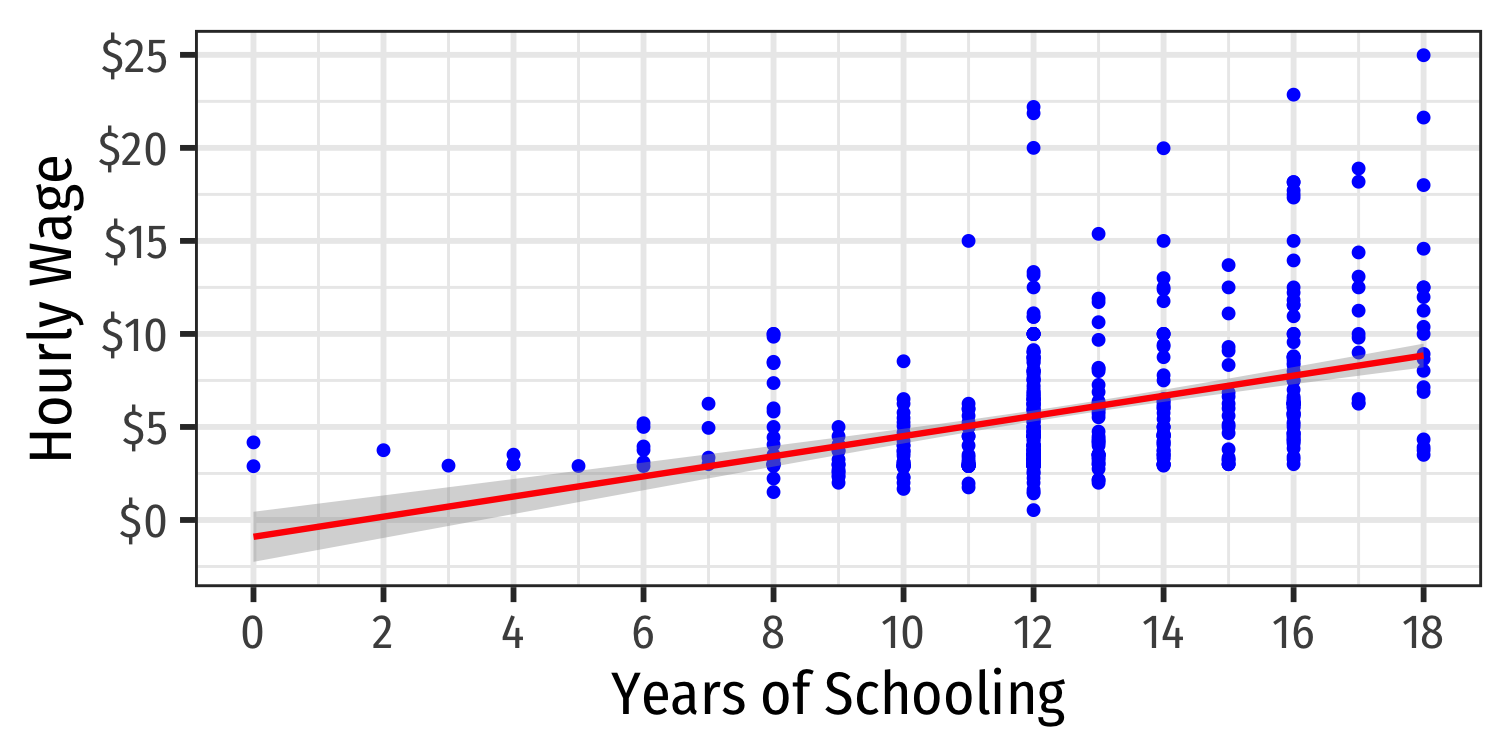
What Might Cause Heteroskedastic Errors?

^wagei=^β0+^β1educi

Wage
Intercept -0.90    
(0.68)   
Years of Schooling 0.54 ***
(0.05)   
N 526       
R-Squared 0.16    
SER 3.38    
*** p < 0.001; ** p < 0.01; * p < 0.05.

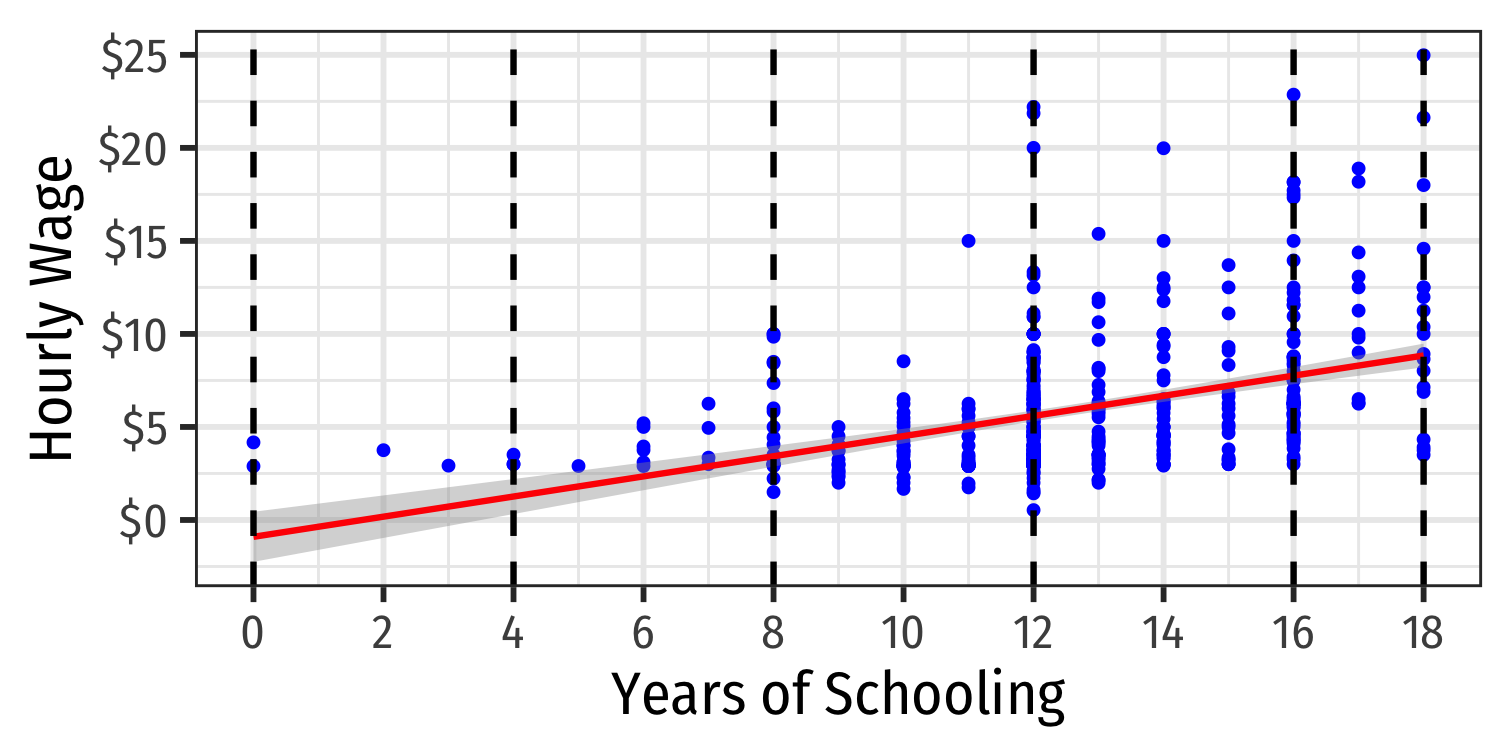
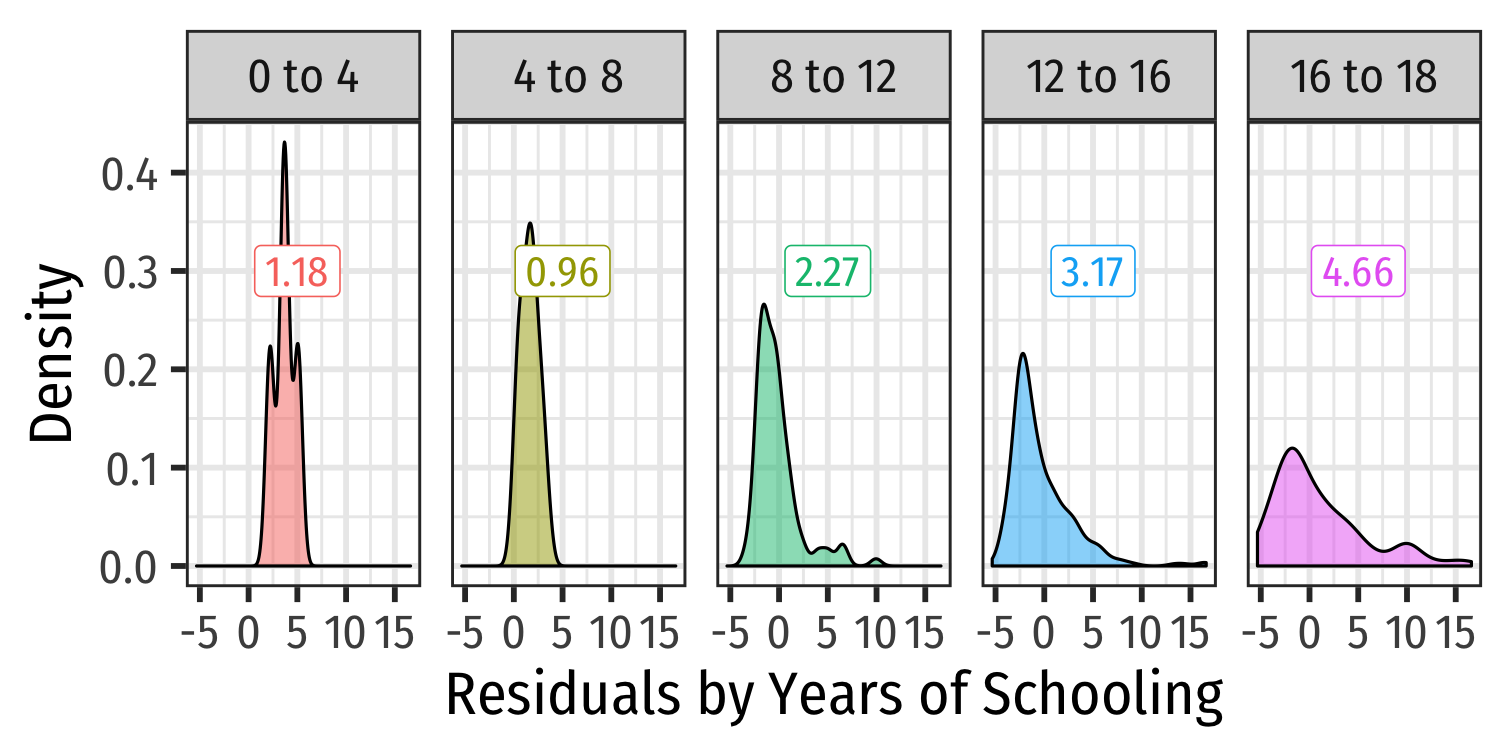
Detecting Heteroskedasticity I

  • Several tests to check if data is heteroskedastic
  • One common test is Breusch-Pagan test
  • Can use bptest() with lmtest package in R
    • H0: homoskedastic
    • If p-value < 0.05, reject H0⟹ heteroskedastic

Detecting Heteroskedasticity I

  • Several tests to check if data is heteroskedastic
  • One common test is Breusch-Pagan test
  • Can use bptest() with lmtest package in R
    • H0: homoskedastic
    • If p-value < 0.05, reject H0⟹ heteroskedastic
# install.packages("lmtest")
library("lmtest")
bptest(school_reg)
## 
##     studentized Breusch-Pagan test
## 
## data:  school_reg
## BP = 5.7936, df = 1, p-value = 0.01608

Detecting Heteroskedasticity II

  • How about our wage regression?
# install.packages("lmtest")
library("lmtest")
bptest(wage_reg)
## 
##     studentized Breusch-Pagan test
## 
## data:  wage_reg
## BP = 15.306, df = 1, p-value = 9.144e-05

Fixing Heteroskedasticity I

  • Heteroskedasticity is easy to fix with software that can calculate robust standard errors (using the more complicated formula above)

  • Easiest method is to use estimatr package

    • lm_robust() command (instead of lm) to run regression
    • set se_type="stata" to calculate robust SEs using the formula above
#install.packages("estimatr")
library(estimatr)
school_reg_robust <-lm_robust(testscr ~ str, data = CASchool,
                              se_type = "stata")
school_reg_robust
##               Estimate Std. Error   t value      Pr(>|t|)   CI Lower
## (Intercept) 698.932952 10.3643599 67.436191 9.486678e-227 678.560192
## str          -2.279808  0.5194892 -4.388557  1.446737e-05  -3.300945
##               CI Upper  DF
## (Intercept) 719.305713 418
## str          -1.258671 418

Fixing Heteroskedasticity II

library(huxtable)
huxreg("Normal" = school_reg,
       "Robust" = school_reg_robust,
       coefs = c("Intercept" = "(Intercept)",
                 "STR" = "str"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 2)
Normal Robust
Intercept 698.93 *** 698.93 ***
(9.47)    (10.36)   
STR -2.28 *** -2.28 ***
(0.48)    (0.52)   
N 420        420       
R-Squared 0.05     0.05    
SER 18.58            
*** p < 0.001; ** p < 0.01; * p < 0.05.

Assumption 3: No Serial Correlation

  • Errors are not correlated across observations: cor(ui,uj)=0∀i≠j

  • For simple cross-sectional data, this is rarely an issue

  • Time-series & panel data nearly always contain serial correlation or autocorrelation between errors

  • Errors may be clustered

    • by group: e.g. all observations from Maryland, all observations from Virginia, etc.
    • by time: GDP in 2006 around the world, GDP in 2008 around the world, etc.

  • We'll deal with these fixes when we talk about panel data (or time-series if necessary)

Outliers

Outliers Can Bias OLS! I

  • Outliers can affect the slope (and intercept) of the line and add bias

    • May be result of human error (measurement, transcribing, etc)
    • May be meaningful and accurate

  • In any case, compare how including/dropping outliers affects regression and always discuss outliers!

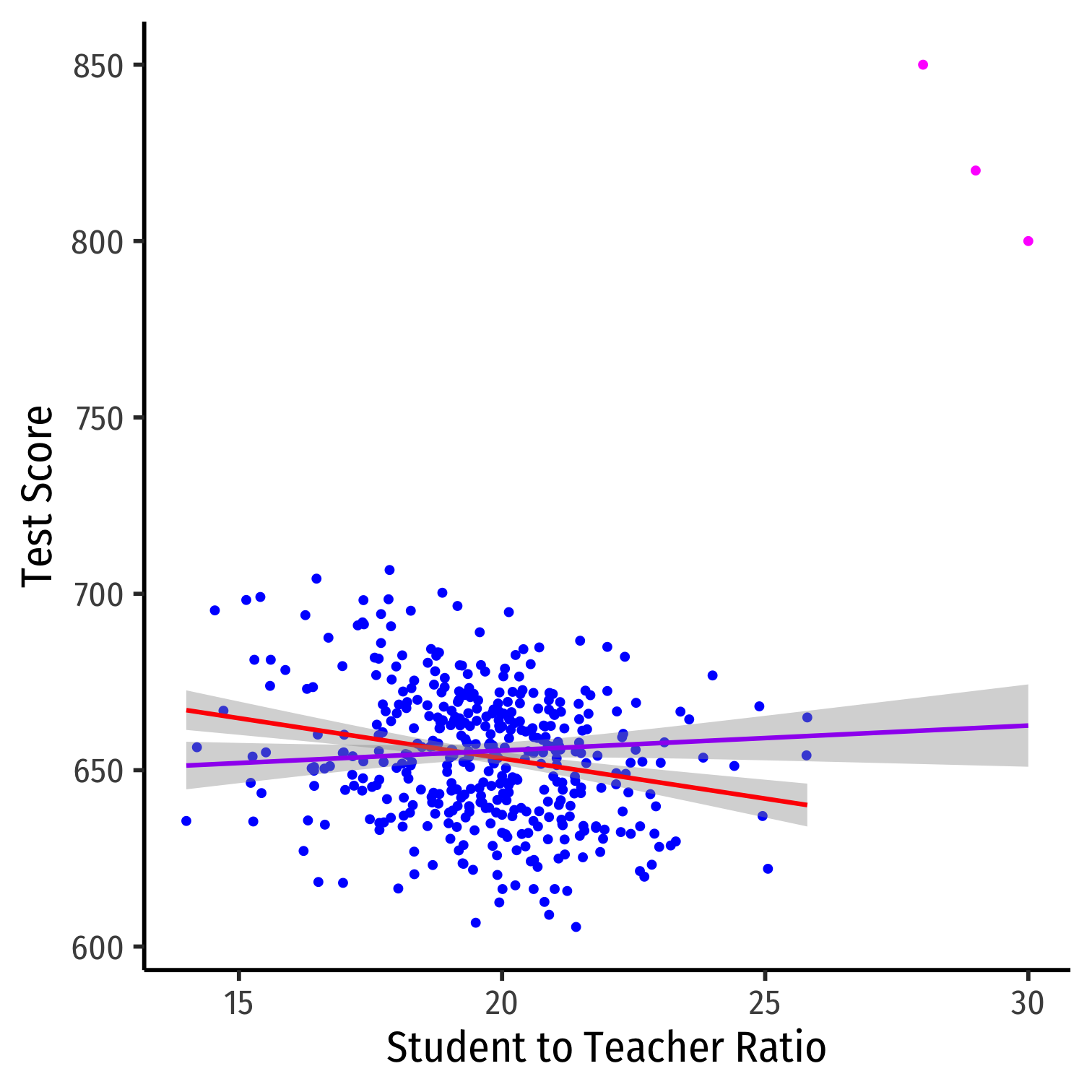
Outliers Can Bias OLS! II

No Outliers Outliers
Intercept 698.93 *** 641.40 ***
(9.47)    (11.21)   
STR -2.28 *** 0.71    
(0.48)    (0.57)   
N 420        423       
R-Squared 0.05     0.00    
SER 18.58     23.76    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Detecting Outliers

  • The car package has an outlierTest command to run on the regression
library("car")
# Use Bonferonni test 
outlierTest(school_outlier_reg) # will point out which obs #s seem outliers
##     rstudent unadjusted p-value Bonferroni p
## 422 8.822768         3.0261e-17   1.2800e-14
## 423 7.233470         2.2493e-12   9.5147e-10
## 421 6.232045         1.1209e-09   4.7414e-07

The Sampling Distribution of ^β1

^β1∼N(E[^β1],σ^β1)

  1. E[^β1]; the center of the distribution (last class)
    • E[^β1]=β11

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow