2.4: OLS: Goodness of Fit and Bias
ECON 480 · Econometrics · Fall 2019
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsf19
metricsF19.classes.ryansafner.com
Goodness of Fit
Models
"All models are wrong. But some are useful." - George Box
Models
"All models are wrong. But some are useful." - George Box
All of Statistics:
Observedi=Modeli+Errori
Goodness of Fit
How well does a line fit data? How tightly clustered around the line are the data points?
Quantify how much variation in Yi is "explained" by the model
Goodness of Fit
How well does a line fit data? How tightly clustered around the line are the data points?
Quantify how much variation in Yi is "explained" by the model
Yi⏟Observed=^Yi⏟Model+ˆu⏟Error
- Recall OLS estimators are chosen specifically to minimize the Sum of Squared Errors (SSE): (n∑i=1^ui2)
Goodness of Fit: R2
- Primary measure1 is regression R-squared, the fraction of variation in Y explained by variation in predicted values
R2= variation in ^Yivariation in Yi
1 Sometimes called the "coefficient of determination"
Goodness of Fit: R2 Formula
R2=ESSTSS
Goodness of Fit: R2 Formula
R2=ESSTSS
- Explained Sum of Squares (ESS):1 sum of squared deviations of predicted values from their mean2
Goodness of Fit: R2 Formula
R2=ESSTSS
- Explained Sum of Squares (ESS):1 sum of squared deviations of predicted values from their mean2
ESS=n∑i=1(^Yi−ˉY)2
Goodness of Fit: R2 Formula
R2=ESSTSS
- Explained Sum of Squares (ESS):1 sum of squared deviations of predicted values from their mean2
ESS=n∑i=1(^Yi−ˉY)2
- Total Sum of Squares (TSS): sum of squared deviations of observed values from their mean
Goodness of Fit: R2 Formula
R2=ESSTSS
- Explained Sum of Squares (ESS):1 sum of squared deviations of predicted values from their mean2
ESS=n∑i=1(^Yi−ˉY)2
- Total Sum of Squares (TSS): sum of squared deviations of observed values from their mean
TSS=n∑i=1(Yi−ˉY)2
1 Sometimes called Model Sum of Squares (MSS) or Regression Sum of Squares (RSS) in other textbooks
2 It can be shown that ¯^Yi=ˉY
Goodness of Fit: R2 Formula II
- Equivalently, the complement of the fraction of unexplained variation in Yi
R2=1−SSETSS
- Equivalently, the square of the correlation coefficient between X and Y:
Goodness of Fit: R2 Formula II
- Equivalently, the complement of the fraction of unexplained variation in Yi
R2=1−SSETSS
- Equivalently, the square of the correlation coefficient between X and Y:
R2=(rX,Y)2
Calculating R2 in R I
- If we wanted to calculate it manually:
# as squared correlation coefficient# Base Rcor(CASchool$testscr, CASchool$str)^2## [1] 0.0512401# dplyrCASchool %>% summarize(r_sq = cor(testscr,str)^2)## # A tibble: 1 x 1## r_sq## <dbl>## 1 0.0512Calculating R2 in R II
- Recall
broom'saugment()command makes a lot of new regression-based values, such as:.fitted: predicted values (^Yi).resid: residuals (^ui)
library(broom)school_reg %>% augment() %>% head(., n=5) # show first 5 values## # A tibble: 5 x 9## testscr str .fitted .se.fit .resid .hat .sigma .cooksd .std.resid## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 691. 17.9 658. 1.24 32.7 0.00442 18.5 0.00689 1.76 ## 2 661. 21.5 650. 1.28 11.3 0.00475 18.6 0.000893 0.612## 3 644. 18.7 656. 1.01 -12.7 0.00297 18.6 0.000700 -0.685## 4 648. 17.4 659. 1.42 -11.7 0.00586 18.6 0.00117 -0.629## 5 641. 18.7 656. 1.02 -15.5 0.00301 18.6 0.00105 -0.836Calculating R2 in R III
- We can calculate
Ras the ratio of variances in model vs. actual (i.e. akin to ESSTSS)
# as ratio of variancesschool_reg %>% augment() %>% summarize(r_sq = var(.fitted)/var(testscr)) # var. of *predicted* testscr over var. of *actual* testscr## # A tibble: 1 x 1## r_sq## <dbl>## 1 0.0512Goodness of Fit: Standard Error of the Regression
- The Standard Error of the Regression, ˆσ or ˆσu is an estimator of the standard deviation of ui
Goodness of Fit: Standard Error of the Regression
- The Standard Error of the Regression, ˆσ or ˆσu is an estimator of the standard deviation of ui
^σu=√SSEn−2
Goodness of Fit: Standard Error of the Regression
- The Standard Error of the Regression, ˆσ or ˆσu is an estimator of the standard deviation of ui
^σu=√SSEn−2
- Measures the average size of the residuals (distance between a data point and the regression line)
- Degrees of Freedom correction of n−2: we use up 2 df to first calculate ^β0 and ^β1!
Calculating SER in R
school_reg %>% augment() %>% summarize(SSE = sum(.resid^2), df = n()-1-1, SER = sqrt(SSE/df))## # A tibble: 1 x 3## SSE df SER## <dbl> <dbl> <dbl>## 1 144315. 418 18.6Calculating SER in R
school_reg %>% augment() %>% summarize(SSE = sum(.resid^2), df = n()-1-1, SER = sqrt(SSE/df))## # A tibble: 1 x 3## SSE df SER## <dbl> <dbl> <dbl>## 1 144315. 418 18.6In large samples (where n−2 is very close to n), SER converges to just the standard deviation of the residuals
school_reg %>% augment() %>% summarize(sd_resid = sd(.resid))## # A tibble: 1 x 1## sd_resid## <dbl>## 1 18.6Goodness of Fit: Looking at R I
summary()command inBase Rgives:Multiple R-squaredResidual standard error(SER)- Calculated with a df of n−2
# Base Rsummary(school_reg)## ## Call:## lm(formula = testscr ~ str, data = CASchool)## ## Residuals:## Min 1Q Median 3Q Max ## -47.727 -14.251 0.483 12.822 48.540 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 698.9330 9.4675 73.825 < 2e-16 ***## str -2.2798 0.4798 -4.751 2.78e-06 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 18.58 on 418 degrees of freedom## Multiple R-squared: 0.05124, Adjusted R-squared: 0.04897 ## F-statistic: 22.58 on 1 and 418 DF, p-value: 2.783e-06Goodness of Fit: Looking at R II
# using broomlibrary(broom)glance(school_reg)## # A tibble: 1 x 11## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl>## 1 0.0512 0.0490 18.6 22.6 2.78e-6 2 -1822. 3650. 3663.## # … with 2 more variables: deviance <dbl>, df.residual <int>Goodness of Fit: Looking at R II
# using broomlibrary(broom)glance(school_reg)## # A tibble: 1 x 11## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl>## 1 0.0512 0.0490 18.6 22.6 2.78e-6 2 -1822. 3650. 3663.## # … with 2 more variables: deviance <dbl>, df.residual <int>r.squaredis0.05⟹ about 5% of variation intestscris explained by our modelsigma(SER) is18.6⟹ average test score is about 18.6 points above/below our model's prediction
Goodness of Fit: Looking at R II
# using broomlibrary(broom)glance(school_reg)## # A tibble: 1 x 11## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl>## 1 0.0512 0.0490 18.6 22.6 2.78e-6 2 -1822. 3650. 3663.## # … with 2 more variables: deviance <dbl>, df.residual <int>r.squaredis0.05⟹ about 5% of variation intestscris explained by our modelsigma(SER) is18.6⟹ average test score is about 18.6 points above/below our model's prediction
# extract it if you want with $r.squaredglance(school_reg)$r.squared## [1] 0.0512401Bias: The Sampling Distributions of the OLS Estimators
Recall: The Two Big Problems with Data
- We use econometrics to identify causal relationships and make inferences about them
Problem for identification: endogeneity
- X is exogenous if its variation is unrelated to other factors (u) that affect Y
- X is endogenous if its variation is related to other factors (u) that affect Y
Problem for inference: randomness
- Data is random due to natural sampling variation
- Taking one sample of a population will yield slightly different information than another sample of the same population


Distributions of the OLS Estimators
OLS estimators (^β0 and ^β1) are computed from a finite (specific) sample of data
Our OLS model contains 2 sources of randomness:
Distributions of the OLS Estimators
OLS estimators (^β0 and ^β1) are computed from a finite (specific) sample of data
Our OLS model contains 2 sources of randomness:
Modeled randomness: u includes all factors affecting Y other than X
- different samples will have different values of those other factors (ui)
Distributions of the OLS Estimators
OLS estimators (^β0 and ^β1) are computed from a finite (specific) sample of data
Our OLS model contains 2 sources of randomness:
Modeled randomness: u includes all factors affecting Y other than X
- different samples will have different values of those other factors (ui)
- Sampling randomness: different samples will generate different OLS estimators
- Thus, ^β0,^β1 are also random variables, with their own sampling distribution
Inferential Statistics and Sampling Distributions
Inferential statistics analyzes a sample to make inferences about a much larger (unobservable) population
Population: all possible individuals that match some well-defined criterion of interest (people, firms, cities, etc)
- Characteristics about (relationships between variables describing) populations are called parameters
Sample: some portion of the population of interest to represent the whole
- Samples examine part of a population to generate statistics used to estimate population parameters
We almost never can directly study the population, so we model it with our samples

Sampling Basics
Example: Suppose you randomly select 100 people and ask how many hours they spend on the internet each day. You take the mean of your sample, and it comes out to 5.4 hours.
Sampling Basics
Example: Suppose you randomly select 100 people and ask how many hours they spend on the internet each day. You take the mean of your sample, and it comes out to 5.4 hours.
- 5.4 hours is a sample statistic describing the sample
- We are more interested in the corresponding parameter of the relevant population (e.g. all Americans)
Sampling Basics
Example: Suppose you randomly select 100 people and ask how many hours they spend on the internet each day. You take the mean of your sample, and it comes out to 5.4 hours.
- 5.4 hours is a sample statistic describing the sample
We are more interested in the corresponding parameter of the relevant population (e.g. all Americans)
If we take another sample of n=100 people, would we get the same number?
Sampling Basics
Example: Suppose you randomly select 100 people and ask how many hours they spend on the internet each day. You take the mean of your sample, and it comes out to 5.4 hours.
- 5.4 hours is a sample statistic describing the sample
We are more interested in the corresponding parameter of the relevant population (e.g. all Americans)
If we take another sample of n=100 people, would we get the same number?
Roughly, but probably not exactly
Sampling variability describes the effect of a statistic varying somewhat from sample to sample
- This is normal, not the result of any error or bias!
I.I.D. Samples
If we collect many samples, and each sample is randomly drawn from the population (and then replaced), then the distribution of samples is said to be independently and identically distributed (i.i.d.)
Each sample is independent of each other sample (due to replacement)
Each sample comes from the identical underlying population distribution

The Sampling Distribution of OLS Estimators
Calculating OLS estimators for a sample makes the OLS estimators themselves random variables:
Draw of i is random ⟹ value of each (Xi,Yi) is random ⟹ ^β0,^β1 are random
Taking different samples will create different values of ^β0,^β1
Therefore, ^β0,^β1 each have a sampling distribution across different samples

The Central Limit Theorem
- Central Limit Theorem (CLT): if we collect samples of size n from the same population and generate a sample statistic (e.g. OLS estimator), then with large enough n, the distribution of the sample statistic is approximately normal IF
- n≥30
- Samples come from a known normal distribution ∼N(μ,σ)
The Central Limit Theorem
- Central Limit Theorem (CLT): if we collect samples of size n from the same population and generate a sample statistic (e.g. OLS estimator), then with large enough n, the distribution of the sample statistic is approximately normal IF
- n≥30
- Samples come from a known normal distribution ∼N(μ,σ)
If neither of these are true, we have other methods (coming shortly!)
One of the most fundamental principles in all of statistics
Allows for virtually all testing of statistical hypotheses → estimating probabilities of values on a normal distribution
The Sampling Distribution of ^β1 I
The CLT allows us to approximate the sampling distributions of ^β0 and ^β1 as normal
We care about ^β1 (slope) since it has economic meaning, rarely about ^β0 (intercept)
^β1∼N(E[^β1],σ^β1)
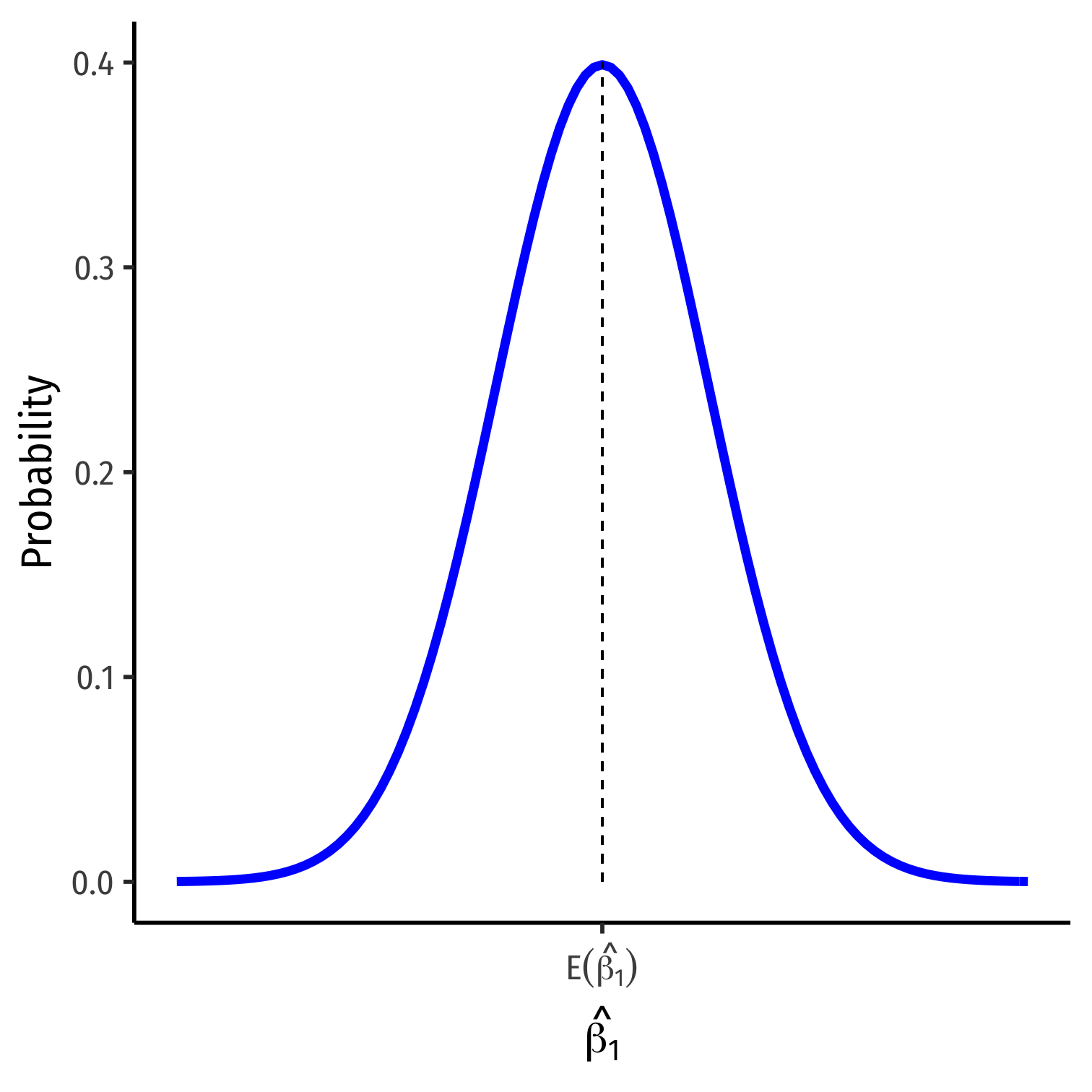
The Sampling Distribution of ^β1 II
^β1∼N(E[^β1],σ^β1)
- We want to know:
E[^β1]; what is the center of the distribution? (today)
σ^β1; how precise is our estimate? (next class)
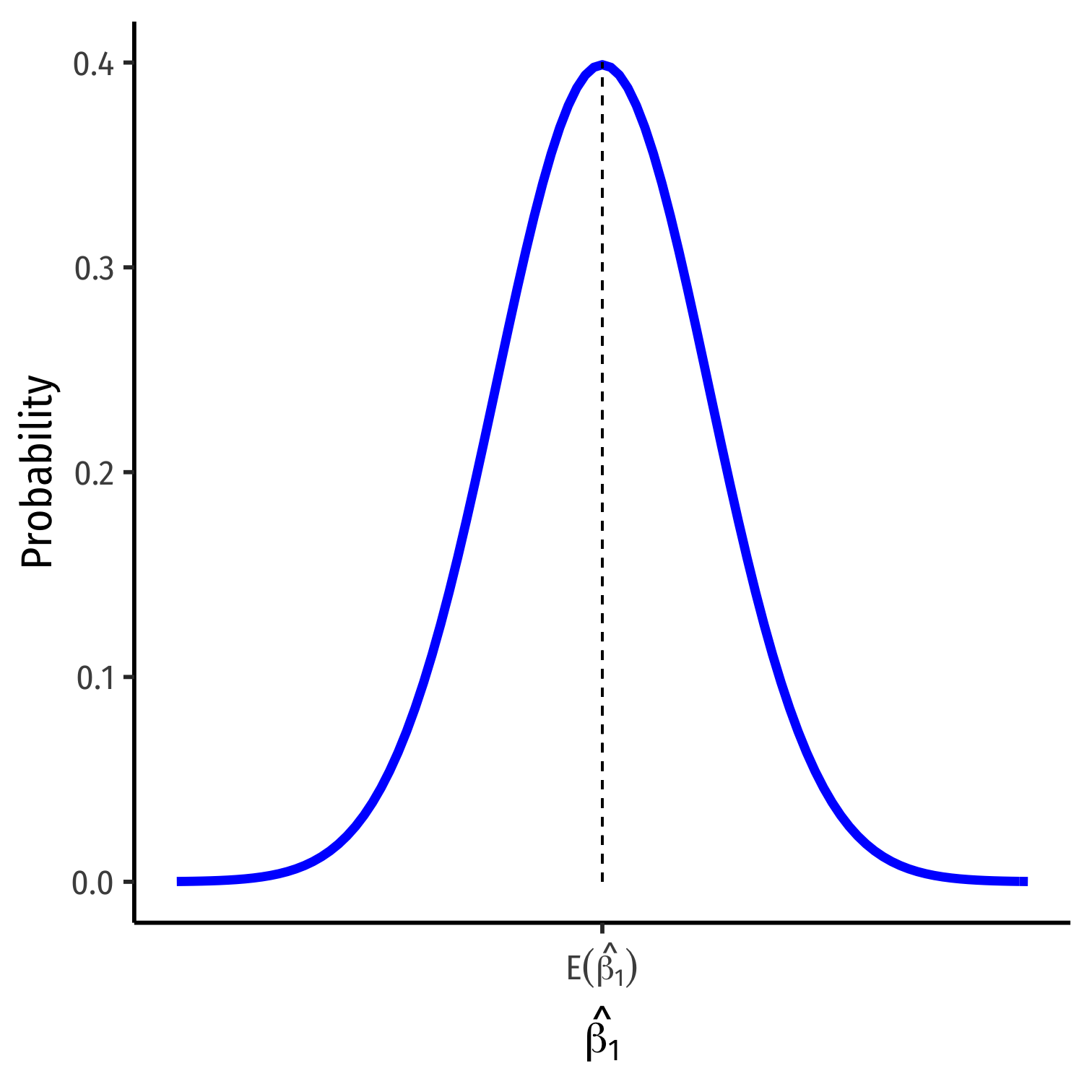
Bias and Exogeneity
Assumptions about Errors I
In order to talk about E[^β1], we need to talk about u
Recall: u is a random variable, and we can never measure the error term

Assumptions about Errors II
- We make 4 critical assumptions about u:
- The expected value of the residuals is 0
E[u]=0

Assumptions about Errors II
- We make 4 critical assumptions about u:
- The expected value of the residuals is 0
E[u]=0

Assumptions about Errors II
- We make 4 critical assumptions about u:
The expected value of the residuals is 0 E[u]=0
The variance of the residuals over X is constant, written: var(u|X)=σ2u

Assumptions about Errors II
- We make 4 critical assumptions about u:
The expected value of the residuals is 0 E[u]=0
The variance of the residuals over X is constant, written: var(u|X)=σ2u
Errors are not correlated across observations: cor(ui,uj)=0∀i≠j

Assumptions about Errors II
- We make 4 critical assumptions about u:
The expected value of the residuals is 0 E[u]=0
The variance of the residuals over X is constant, written: var(u|X)=σ2u
Errors are not correlated across observations: cor(ui,uj)=0∀i≠j
There is no correlation between X and the error term: cor(X,u)=0 or E[u|X]=0

Assumptions 1 and 2: Errors are i.i.d.
The expected value of the residuals is 0 E[u]=0
The variance of the residuals over X is constant, written: var(u|X)=σ2u
- The first two assumptions ⟹ errors are i.i.d., drawn from the same distribution with mean 0 and variance σ2u

Assumption 2: Homoskedasticity
The variance of the residuals over X is constant, written: var(u|X)=σ2u
Assumption 2 implies that errors are "homoskedastic:" they have the same variance across X
Often this assumption is violated: errors may be "heteroskedastic:" they do not have the same variance across X
This is a problem for inference, but we have a simple fix for this (coming shortly)

Assumption 3: No Serial Correlation
Errors are not correlated across observations: cor(ui,uj)=0∀i≠j
For simple cross-sectional data, this is rarely an issue
Time-series & panel data nearly always contain serial correlation or autocorrelation between errors
e.g. "this week's sales look a lot like last weel's sales, which look like...etc"
There are fixes to deal with autocorrelation (coming much later)

Assumption 4: The Zero Conditional Mean Assumption
There is no correlation between X and the error term: cor(X,u)=0
This is the absolute killer assumption, because it assumes exogeneity
Often called the Zero Conditional Mean assumption: E[u|X]=0
"Does knowing X give me any useful information about u?"
- If yes: model is endogenous, biased and not-causal!

Exogeneity and Unbiasedness
- ^β1 is unbiased iff no systematic difference, on average, between sample values of ^β1 and true population β1, i.e.
E[^β1]=β1
Exogeneity and Unbiasedness
- ^β1 is unbiased iff no systematic difference, on average, between sample values of ^β1 and true population β1, i.e.
E[^β1]=β1
Does not mean any sample gives us ^β1=β1, only the estimation procedure will, on average, yield the correct value
Random errors above and below the true value cancel out (so that on average, E[ˆu|X]=0)
Sidenote: Estimators of Statistics I
- In statistics, an estimator is simply a rule that for calculating a statistic (often about a wider population parameter)
Sidenote: Estimators of Statistics I
- In statistics, an estimator is simply a rule that for calculating a statistic (often about a wider population parameter)
Example: We want to estimate the average height (H) of U.S. adults (population) and have a random sample of 100 adults.
Sidenote: Estimators of Statistics I
- In statistics, an estimator is simply a rule that for calculating a statistic (often about a wider population parameter)
Example: We want to estimate the average height (H) of U.S. adults (population) and have a random sample of 100 adults.
Calculate the mean height of our sample (ˉH) to estimate the true mean height of the population (μH)
ˉH is an estimator of μH
Sidenote: Estimators of Statistics I
- In statistics, an estimator is simply a rule that for calculating a statistic (often about a wider population parameter)
Example: We want to estimate the average height (H) of U.S. adults (population) and have a random sample of 100 adults.
Calculate the mean height of our sample (ˉH) to estimate the true mean height of the population (μH)
ˉH is an estimator of μH
There are many estimators we could use to estimate μH
- How about using the first value in our sample: H1
Sidenote: Estimators of Statistics II
- What makes one estimator (e.g. ˉH) better than another (e.g. H1)?1
Biasedness: does the estimator give us the true parameter on average?
Efficiency: an estimator with a smaller variance is better

1 Technically, we also care about consistency: minimizing uncertainty about the correct value. The Law of Large Numbers, similar to CLT, permits this. We don't need to get too advanced about probability in this class.
Exogeneity and Unbiasedness I
^β1 is the Best Linear Unbiased Estimator (BLUE) estimator of β1 when X is exogenous1
No systematic difference, on average, between sample values of ^β1 and the true population β1:
E[^β1]=β1
- Does not mean that each sample gives us ^β1=β1, only the estimation procedure will, on average, yield the correct value

1 The proof for this is known as the Gauss-Markov Theorem. See today's class notes for a simplified proof.
Exogeneity and Unbiasedness II
- Recall, an exogenous variable (X) is unrelated to other factors affecting Y, i.e.:
cor(X,u)=0
Exogeneity and Unbiasedness II
- Recall, an exogenous variable (X) is unrelated to other factors affecting Y, i.e.:
cor(X,u)=0
- Again, this is called the Zero Conditional Mean Assumption
E(u|X)=0
Exogeneity and Unbiasedness II
- Recall, an exogenous variable (X) is unrelated to other factors affecting Y, i.e.:
cor(X,u)=0
- Again, this is called the Zero Conditional Mean Assumption
E(u|X)=0
For any known value of X, the expected value of u is 0
Knowing the value of X must tell us nothing about the value of u (anything else relevant to Y other than X)
We can then confidently assert causation: X→Y
Endogeneity and Bias
- Nearly all independent variables are endogenous, they are related to the error term u
cor(X,u)≠0
Endogeneity and Bias
- Nearly all independent variables are endogenous, they are related to the error term u
cor(X,u)≠0
Example: Suppose we estimate the following relationship:
Violent crimest=β0+β1Ice cream salest+ut
We find ^β1>0
Does this mean Ice cream sales$\rightarrow$Violent crimes?
Endogeneity and Bias III
- The true expected value of ^β1 is actually:1
E[^β1]=β1+cor(X,u)σuσX
Endogeneity and Bias III
- The true expected value of ^β1 is actually:1
E[^β1]=β1+cor(X,u)σuσX
- Takeaways:
Endogeneity and Bias III
- The true expected value of ^β1 is actually:1
E[^β1]=β1+cor(X,u)σuσX
- Takeaways:
- If X is exogenous: cor(X,u)=0, we're just left with β1
Endogeneity and Bias III
- The true expected value of ^β1 is actually:1
E[^β1]=β1+cor(X,u)σuσX
- Takeaways:
If X is exogenous: cor(X,u)=0, we're just left with β1
The larger cor(X,u) is, larger bias: (E[^β1]−β1)
Endogeneity and Bias III
- The true expected value of ^β1 is actually:1
E[^β1]=β1+cor(X,u)σuσX
- Takeaways:
If X is exogenous: cor(X,u)=0, we're just left with β1
The larger cor(X,u) is, larger bias: (E[^β1]−β1)
We can "sign" the direction of the bias based on cor(X,u)
- Positive cor(X,u) overestimates the true β1 (^β1 is too high)
- Negative cor(X,u) underestimates the true β1 (^β1 is too low)
1 See today's class notes for proof.
Endogeneity and Bias: Example I
Example: wagesi=β0+β1educationi+u
Is this an accurate reflection of educ→wages?
Does E[u|education]=0?
What would E[u|education]>0 mean?
Endogeneity and Bias: Example II
Example: per capita cigarette consumption=β0+β1State cig tax rate+u
Is this an accurate reflection of tax→cons?
Does E[u|tax]=0?
What would E[u|tax]>0 mean?
Exogeneity and RCTs
Think about an idealized randomized controlled experiment
Subjects randomly assigned to treatment or control group
Implies knowing whether someone is treated (X) tells us nothing about their personal characteristics (u)
Random assignment makes u independent of X, so
cor(X,u)=0 and E[u|X]=0
