2.3: OLS Linear Regression
ECON 480 · Econometrics · Fall 2019
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsf19
metricsF19.classes.ryansafner.com
Exploring Relationships
Bivariate Data and Relationships
- We looked at single variables for descriptive statistics
- Most uses of statistics in economics and business investigate relationships between variables
Examples
- # of police & crime rates
- healthcare spending & life expectancy
- government spending & GDP growth
- carbon dioxide emissions & temperatures
- We will begin with bivariate data for relationships between X and Y
- Immediate aim is to explore associations between variables, quantified with correlation and linear regression
- Later we want to develop more sophisticated tools to argue for causation
Bivariate Data: Spreadsheets I
econfreedom <- read_csv("../data/econfreedom.csv")head(econfreedom)## # A tibble: 6 x 6## X1 Country ISO ef gdp continent## <dbl> <chr> <chr> <dbl> <dbl> <chr> ## 1 1 Albania ALB 7.4 4543. Europe ## 2 2 Algeria DZA 5.15 4784. Africa ## 3 3 Angola AGO 5.08 4153. Africa ## 4 4 Argentina ARG 4.81 10502. Americas ## 5 5 Australia AUS 7.93 54688. Oceania ## 6 6 Austria AUT 7.56 47604. Europe- Rows are individual observations
- Columns are variables on all individuals
Bivariate Data: Spreadsheets II
econfreedom %>% glimpse()## Observations: 112## Variables: 6## $ X1 <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,…## $ Country <chr> "Albania", "Algeria", "Angola", "Argentina", "Australi…## $ ISO <chr> "ALB", "DZA", "AGO", "ARG", "AUS", "AUT", "BHR", "BGD"…## $ ef <dbl> 7.40, 5.15, 5.08, 4.81, 7.93, 7.56, 7.60, 6.35, 7.51, …## $ gdp <dbl> 4543.0880, 4784.1943, 4153.1463, 10501.6603, 54688.445…## $ continent <chr> "Europe", "Africa", "Africa", "Americas", "Oceania", "…Bivariate Data: Spreadsheets III
source("../files/summaries.R") # use my summary_table functioneconfreedom %>% summary_table(ef, gdp)| Variable | Obs | Min | Q1 | Median | Q3 | Max | Mean | Std. Dev. |
|---|---|---|---|---|---|---|---|---|
| ef | 112 | 4.81 | 6.42 | 7.0 | 7.40 | 8.71 | 6.86 | 0.78 |
| gdp | 112 | 206.71 | 1307.46 | 5123.3 | 17302.66 | 89590.81 | 14488.49 | 19523.54 |
Bivariate Data: Scatterplots
The best way to visualize an association between two variables is with a scatterplot
Each point: pair of variable values (xi,yi)∈X,Y for observation i
library("ggplot2")ggplot(data = econfreedom)+ aes(x = ef, y = gdp)+ geom_point(aes(color = continent), size = 2)+ labs(x = "Economic Freedom Index (2014)", y = "GDP per Capita (2014 USD)", color = "")+ theme_bw(base_family = "Fira Sans Condensed", base_size=20)+ theme(legend.position = "bottom")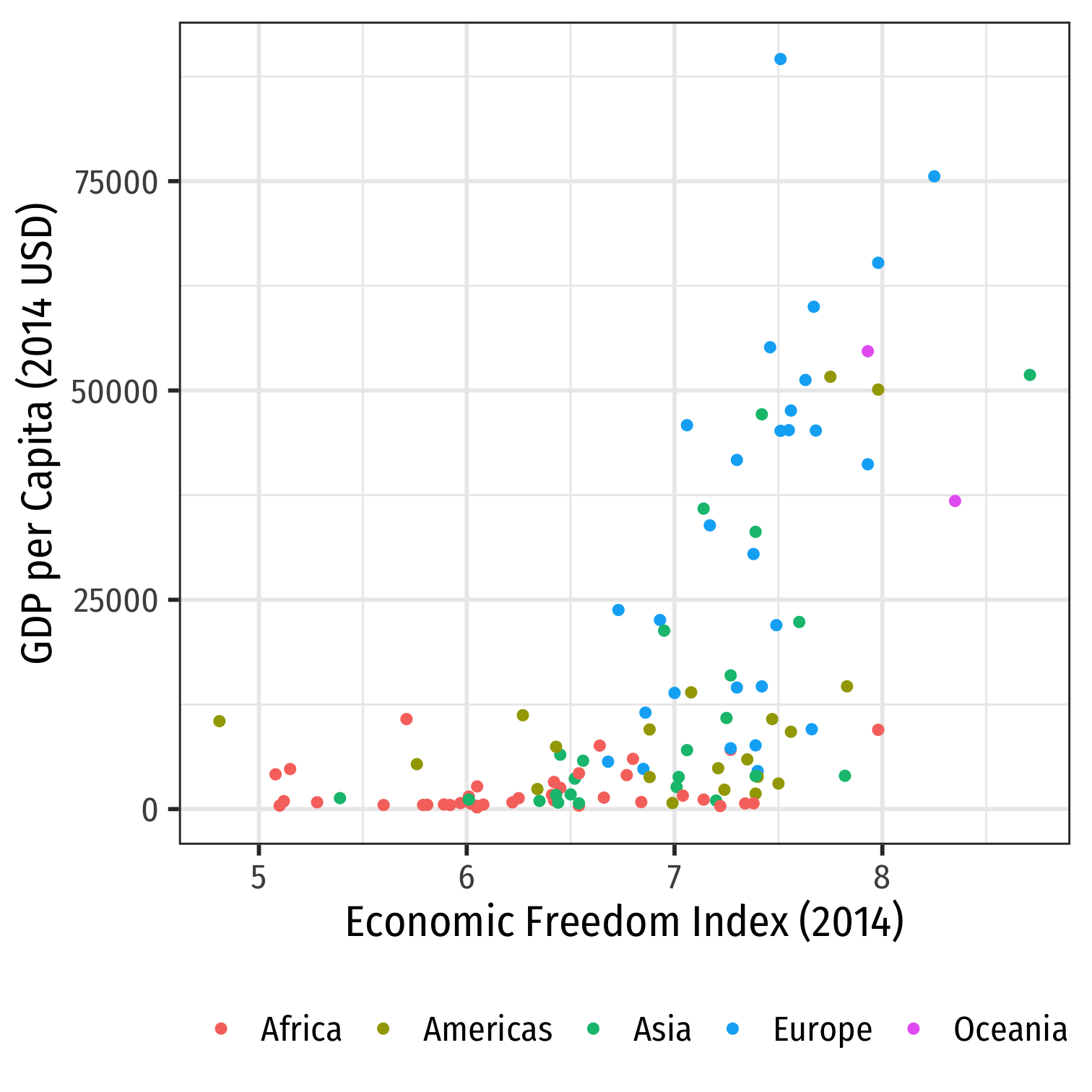
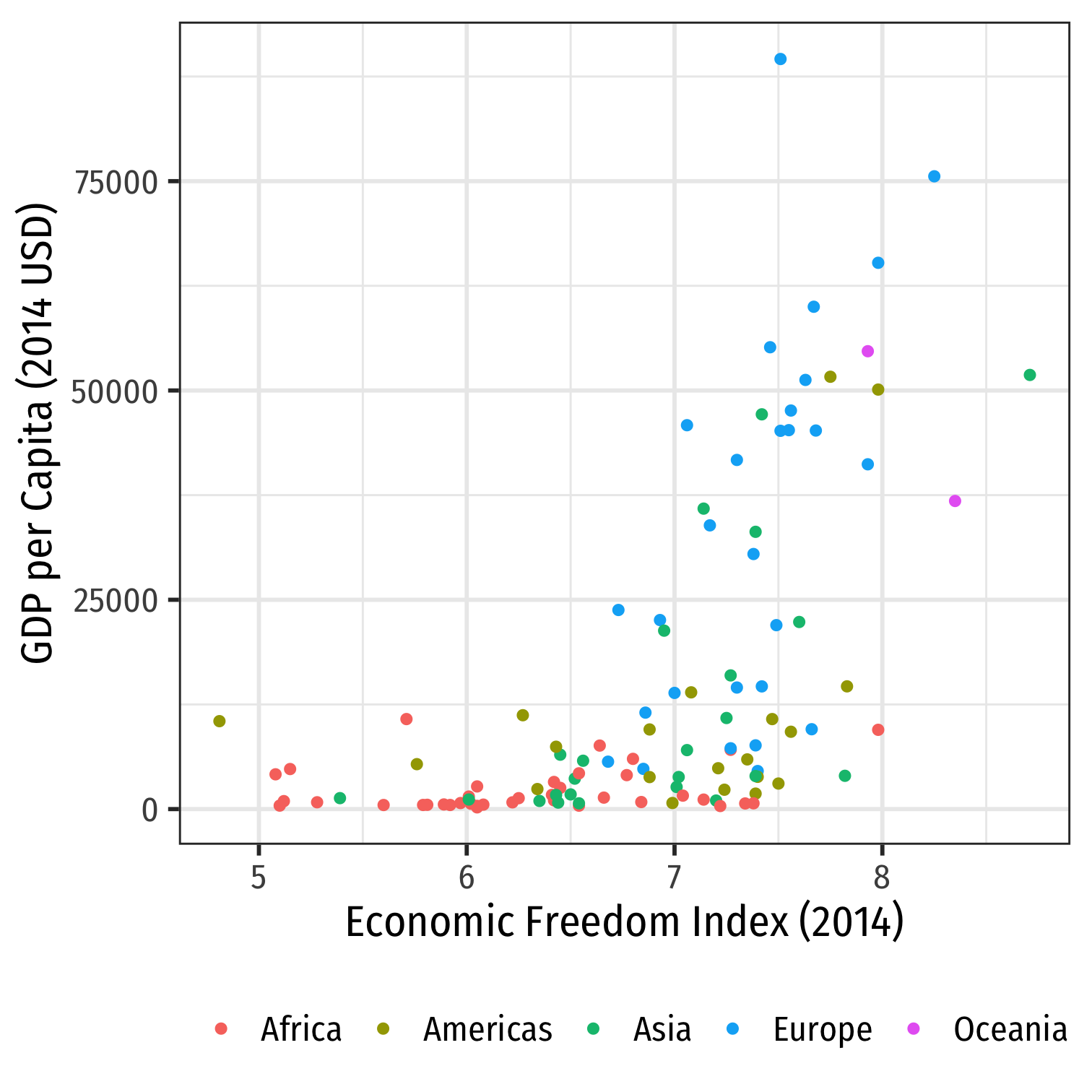
Associations
- Look for association between independent and dependent variables
Direction: is the trend positive or negative?
Form: is the trend linear, quadratic, something else, or no pattern?
Strength: is the association strong or weak?
Outliers: do any observations break the trends above?
Quantifying Relationships
Covariance
- For any two variables, we can measure their sample covariance, cov(X,Y) or sX,Y to quantify how they vary together1
Covariance
- For any two variables, we can measure their sample covariance, cov(X,Y) or sX,Y to quantify how they vary together1
sX,Y=E[(X−ˉX)(Y−ˉY)]
Covariance
- For any two variables, we can measure their sample covariance, cov(X,Y) or sX,Y to quantify how they vary together1
sX,Y=E[(X−ˉX)(Y−ˉY)]
- Intuition: if X is above its mean, would we expect Y:
- to be above its mean also (X and Y covary positively)
- to be below its mean (X and Y covary negatively)
Covariance
- For any two variables, we can measure their sample covariance, cov(X,Y) or sX,Y to quantify how they vary together1
sX,Y=E[(X−ˉX)(Y−ˉY)]
- Intuition: if X is above its mean, would we expect Y:
- to be above its mean also (X and Y covary positively)
- to be below its mean (X and Y covary negatively)
- Covariance is a common measure, but the units are meaningless, thus we rarely need to use it so don't worry about learning the formula
1 Henceforth we limit all measures to samples, for convenience. Population covariance is denoted σX,Y
Covariance, in R
# base R cov(econfreedom$ef,econfreedom$gdp)## [1] 8922.933# dplyr econfreedom %>% summarize(cov = cov(ef,gdp))## # A tibble: 1 x 1## cov## <dbl>## 1 8923.Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, ρ or r ∈[−1,1]
Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, ρ or r ∈[−1,1]
rX,Y=sX,YsXsY=cov(X,Y)sd(X)sd(Y)
Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, ρ or r ∈[−1,1]
rX,Y=sX,YsXsY=cov(X,Y)sd(X)sd(Y)
- Simply weight covariance by the product of the standard deviations of X and Y
Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, ρ or r ∈[−1,1]
rX,Y=sX,YsXsY=cov(X,Y)sd(X)sd(Y)
Simply weight covariance by the product of the standard deviations of X and Y
Alternatively, take the average1 of the product of standardized (Z-scores for) each (xi,yi) pair:2
Correlation
- More convenient to standardize covariance into a more intuitive concept: correlation, ρ or r ∈[−1,1]
rX,Y=sX,YsXsY=cov(X,Y)sd(X)sd(Y)
Simply weight covariance by the product of the standard deviations of X and Y
Alternatively, take the average1 of the product of standardized (Z-scores for) each (xi,yi) pair:2
r=1n−1n∑i=1(xi−ˉXsX)(yi−ˉYsY)r=1n−1n∑i=1ZXZY
1 Over \\(n-1\\), since this is a sample statistic.
2 See today's class notes page for an example of the code for how to calculate correlation "by hand" in R using the second method.
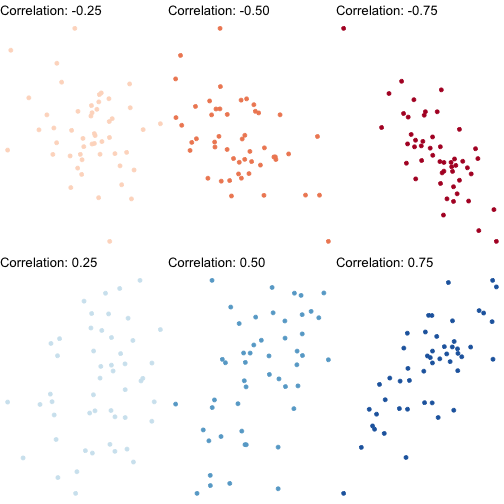
Correlation: Interpretation
- Correlation is standardized to
−1≤r≤1
- Negative values ⟹ negative association
- Positive values ⟹ positive association
- Correlation of 0 ⟹ no association
- As |r|→1⟹ the stronger the association
- Correlation of |r|=1⟹ perfectly linear
Correlation and Covariance in R
# Base r: cov or cor(df$x, df$y)cov(econfreedom$ef, econfreedom$gdp)## [1] 8922.933cor(econfreedom$ef, econfreedom$gdp)## [1] 0.5867018# dplyr econfreedom %>% summarize(covariance = cov(ef, gdp), correlation = cor(ef, gdp))## # A tibble: 1 x 2## covariance correlation## <dbl> <dbl>## 1 8923. 0.587Correlation and Covariance in R I
corrplotis a great package (install and then load) to visualize correlations in data
library(corrplot) # see more at https://github.com/taiyun/corrplotlibrary(RColorBrewer) # for color scheme used herelibrary(gapminder) # for gapminder data# need to make a corelation matrix with cor(); can only include numeric variablesgapminder_cor<- gapminder %>% dplyr::select(gdpPercap, pop, lifeExp)# make a correlation table with cor (base R)gapminder_cor_table<-cor(gapminder_cor)# view itgapminder_cor_tableCorrelation and Covariance in R II
corrplot(gapminder_cor_table, type="upper", method = "circle", # number for showing correlation coefficient order="alphabet", col=brewer.pal(n=8, name="RdBu"))Correlation and Covariance in R II
corrplot(gapminder_cor_table, type="upper", method = "circle", # number for showing correlation coefficient order="alphabet", col=brewer.pal(n=8, name="RdBu"))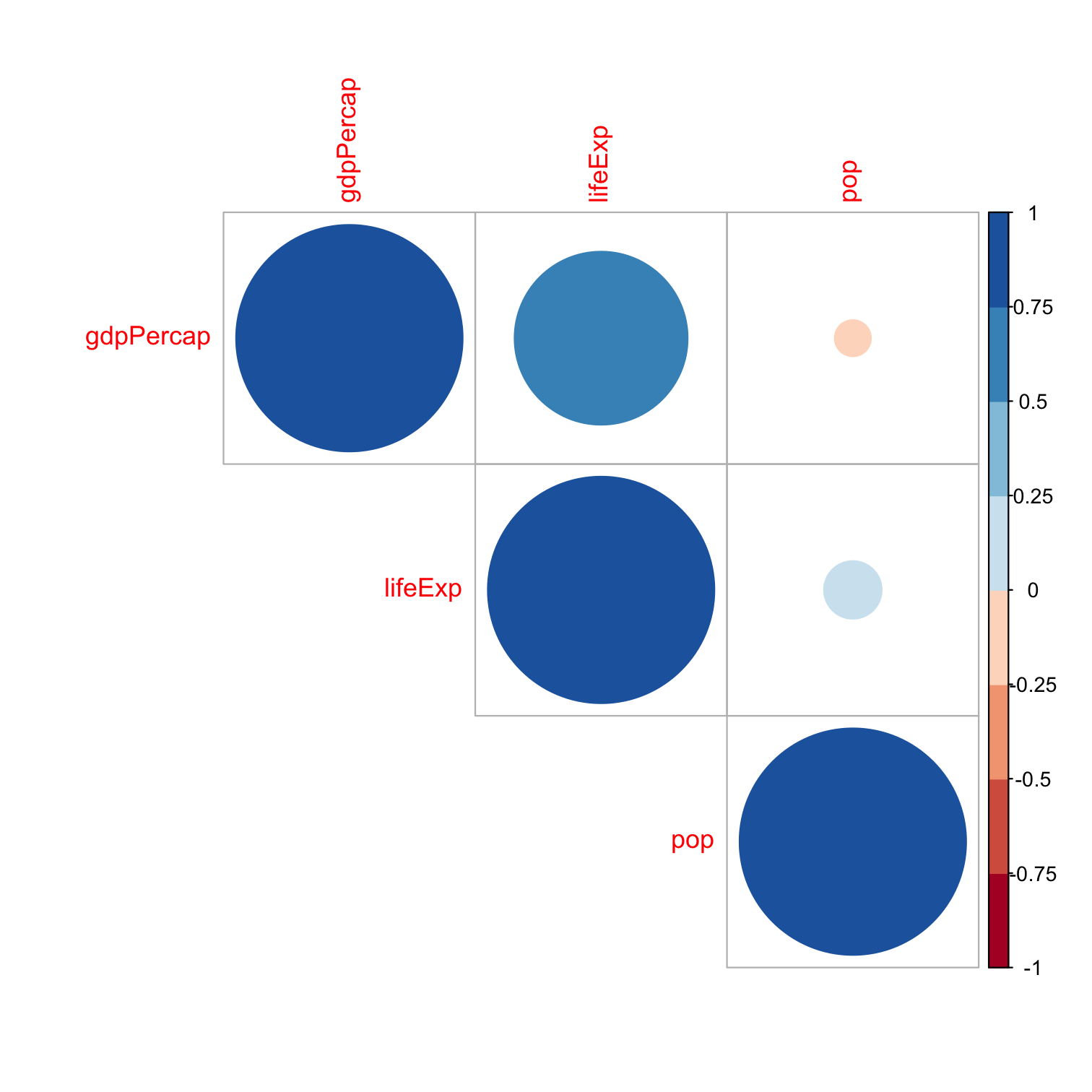
Correlation and Endogeneity
Your Occasional Reminder: Correlation does not imply causation!
- I'll show you the difference in a few weeks (when we can actually talk about causation)
If X and Y are strongly correlated, X can still be endogenous!
See today's class notes page for more on Covariance and Correlation

Always Plot Your Data!

Linear Regression
Fitting a Line to Data
- If an association appears linear, we can estimate the equation of a line that would "fit" the data
Y=a+bX
- Recall a linear equation describing a line contains:1
- a: vertical intercept
- b: slope
1 Note we'll use different symbols for a & b, the standard econometric notation.
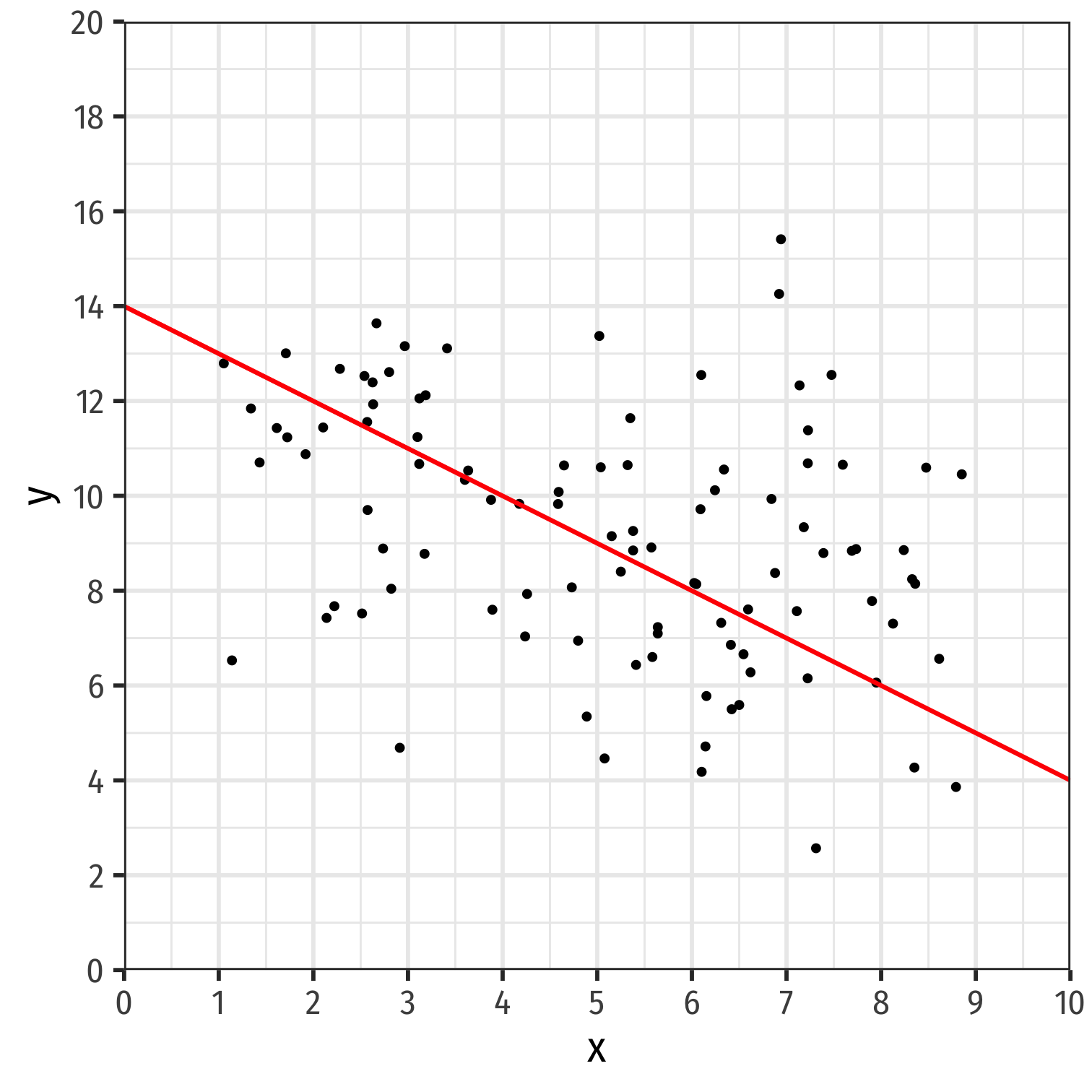
Fitting a Line to Data
- If an association appears linear, we can estimate the equation of a line that would "fit" the data
Y=a+bX
Recall a linear equation describing a line contains:1
- a: vertical intercept
- b: slope
How do we choose the equation that best fits the data?
1 Note we'll use different symbols for a & b, the standard econometric notation.
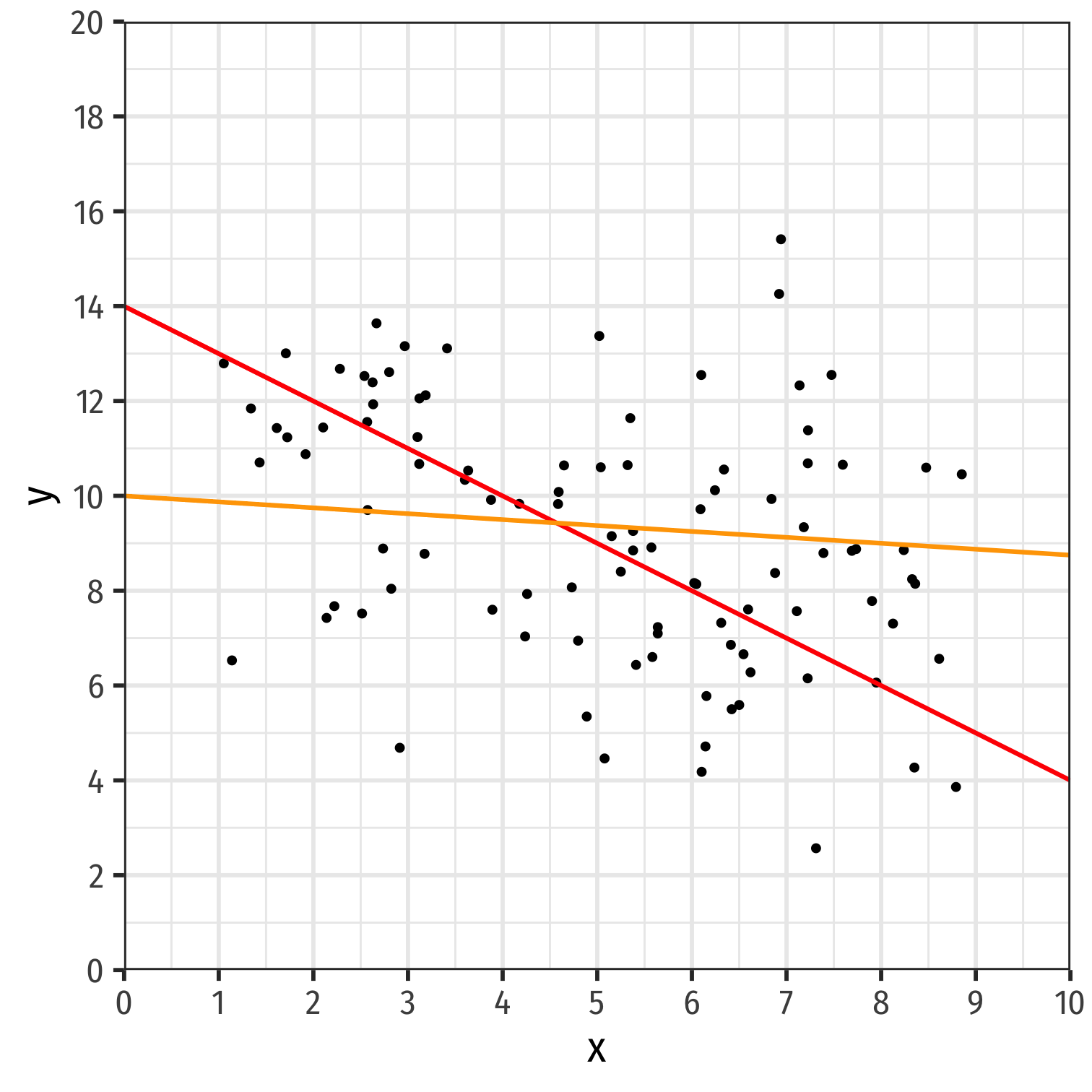
Fitting a Line to Data
- If an association appears linear, we can estimate the equation of a line that would "fit" the data
Y=a+bX
Recall a linear equation describing a line contains:1
- a: vertical intercept
- b: slope
How do we choose the equation that best fits the data?
This process is called linear regression
1 Note we'll use different symbols for a & b, the standard econometric notation.
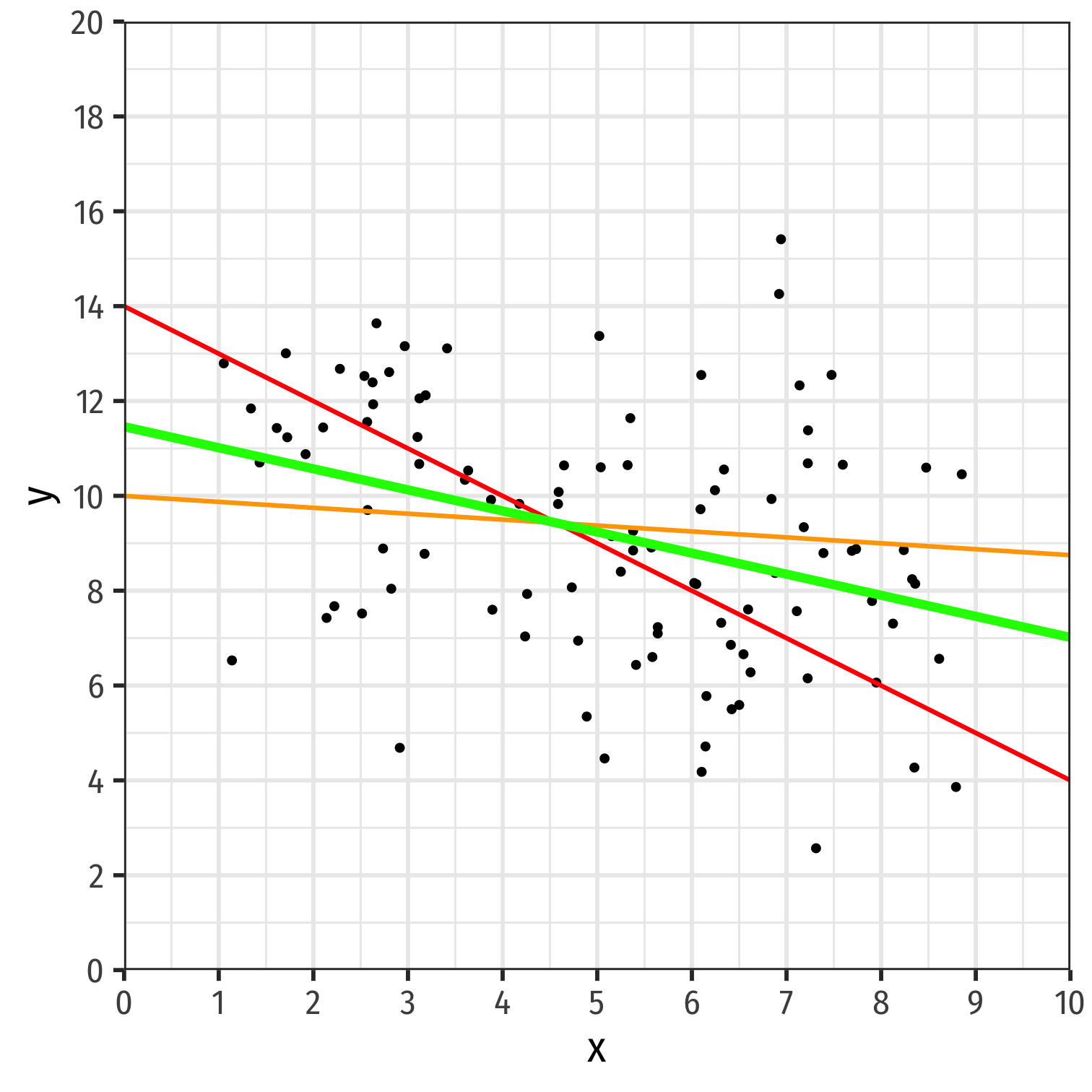
Population Linear Regression Model
Linear regression lets us estimate the slope of the population regression line between X and Y
We can make inferences about the population slope coefficient
eventually, a causal interpretation
slope=ΔYΔX: for a 1-unit change in X, how many units will this cause Y to change?
Class Size Example
Example: What is the relationship between class size and educational performance?

Class Size Example: Load the Data
# install.packages("haven") # install for first uselibrary("haven") # load for importing .dta filesCASchool<-read_dta("../data/caschool.dta")Class Size Example: Look at the Data I
glimpse(CASchool)## Observations: 420## Variables: 21## $ observat <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, …## $ dist_cod <dbl> 75119, 61499, 61549, 61457, 61523, 62042, 68536, 63834,…## $ county <chr> "Alameda", "Butte", "Butte", "Butte", "Butte", "Fresno"…## $ district <chr> "Sunol Glen Unified", "Manzanita Elementary", "Thermali…## $ gr_span <chr> "KK-08", "KK-08", "KK-08", "KK-08", "KK-08", "KK-08", "…## $ enrl_tot <dbl> 195, 240, 1550, 243, 1335, 137, 195, 888, 379, 2247, 44…## $ teachers <dbl> 10.90, 11.15, 82.90, 14.00, 71.50, 6.40, 10.00, 42.50, …## $ calw_pct <dbl> 0.5102, 15.4167, 55.0323, 36.4754, 33.1086, 12.3188, 12…## $ meal_pct <dbl> 2.0408, 47.9167, 76.3226, 77.0492, 78.4270, 86.9565, 94…## $ computer <dbl> 67, 101, 169, 85, 171, 25, 28, 66, 35, 0, 86, 56, 25, 0…## $ testscr <dbl> 690.80, 661.20, 643.60, 647.70, 640.85, 605.55, 606.75,…## $ comp_stu <dbl> 0.34358975, 0.42083332, 0.10903226, 0.34979424, 0.12808…## $ expn_stu <dbl> 6384.911, 5099.381, 5501.955, 7101.831, 5235.988, 5580.…## $ str <dbl> 17.88991, 21.52466, 18.69723, 17.35714, 18.67133, 21.40…## $ avginc <dbl> 22.690001, 9.824000, 8.978000, 8.978000, 9.080333, 10.4…## $ el_pct <dbl> 0.000000, 4.583333, 30.000002, 0.000000, 13.857677, 12.…## $ read_scr <dbl> 691.6, 660.5, 636.3, 651.9, 641.8, 605.7, 604.5, 605.5,…## $ math_scr <dbl> 690.0, 661.9, 650.9, 643.5, 639.9, 605.4, 609.0, 612.5,…## $ aowijef <dbl> 35.77982, 43.04933, 37.39445, 34.71429, 37.34266, 42.81…## $ es_pct <dbl> 1.000000, 3.583333, 29.000002, 1.000000, 12.857677, 11.…## $ es_frac <dbl> 0.01000000, 0.03583334, 0.29000002, 0.01000000, 0.12857…Class Size Example: Look at the Data II
| observat | dist_cod | county | district | gr_span | enrl_tot | teachers | calw_pct | meal_pct | computer | testscr | comp_stu | expn_stu | str | avginc | el_pct | read_scr | math_scr | aowijef | es_pct | es_frac |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 75119 | Alameda | Sunol Glen Unified | KK-08 | 195 | 10.90 | 0.5102 | 2.0408 | 67 | 690.80 | 0.3435898 | 6384.911 | 17.88991 | 22.690001 | 0.000000 | 691.6 | 690.0 | 35.77982 | 1.000000 | 0.0100000 |
| 2 | 61499 | Butte | Manzanita Elementary | KK-08 | 240 | 11.15 | 15.4167 | 47.9167 | 101 | 661.20 | 0.4208333 | 5099.381 | 21.52466 | 9.824000 | 4.583334 | 660.5 | 661.9 | 43.04933 | 3.583334 | 0.0358333 |
| 3 | 61549 | Butte | Thermalito Union Elementary | KK-08 | 1550 | 82.90 | 55.0323 | 76.3226 | 169 | 643.60 | 0.1090323 | 5501.955 | 18.69723 | 8.978000 | 30.000002 | 636.3 | 650.9 | 37.39445 | 29.000002 | 0.2900000 |
| 4 | 61457 | Butte | Golden Feather Union Elementary | KK-08 | 243 | 14.00 | 36.4754 | 77.0492 | 85 | 647.70 | 0.3497942 | 7101.831 | 17.35714 | 8.978000 | 0.000000 | 651.9 | 643.5 | 34.71429 | 1.000000 | 0.0100000 |
| 5 | 61523 | Butte | Palermo Union Elementary | KK-08 | 1335 | 71.50 | 33.1086 | 78.4270 | 171 | 640.85 | 0.1280899 | 5235.988 | 18.67133 | 9.080333 | 13.857677 | 641.8 | 639.9 | 37.34266 | 12.857677 | 0.1285768 |
| 6 | 62042 | Fresno | Burrel Union Elementary | KK-08 | 137 | 6.40 | 12.3188 | 86.9565 | 25 | 605.55 | 0.1824818 | 5580.147 | 21.40625 | 10.415000 | 12.408759 | 605.7 | 605.4 | 42.81250 | 11.408759 | 0.1140876 |
Class Size Example: Scatterplot
scatter<-ggplot(data = CASchool)+ aes(x = str, y = testscr)+ geom_point(color = "blue")+ labs(x = "Student to Teacher Ratio", y = "Test Score")+ theme_bw(base_family = "Fira Sans Condensed", base_size = 20)scatter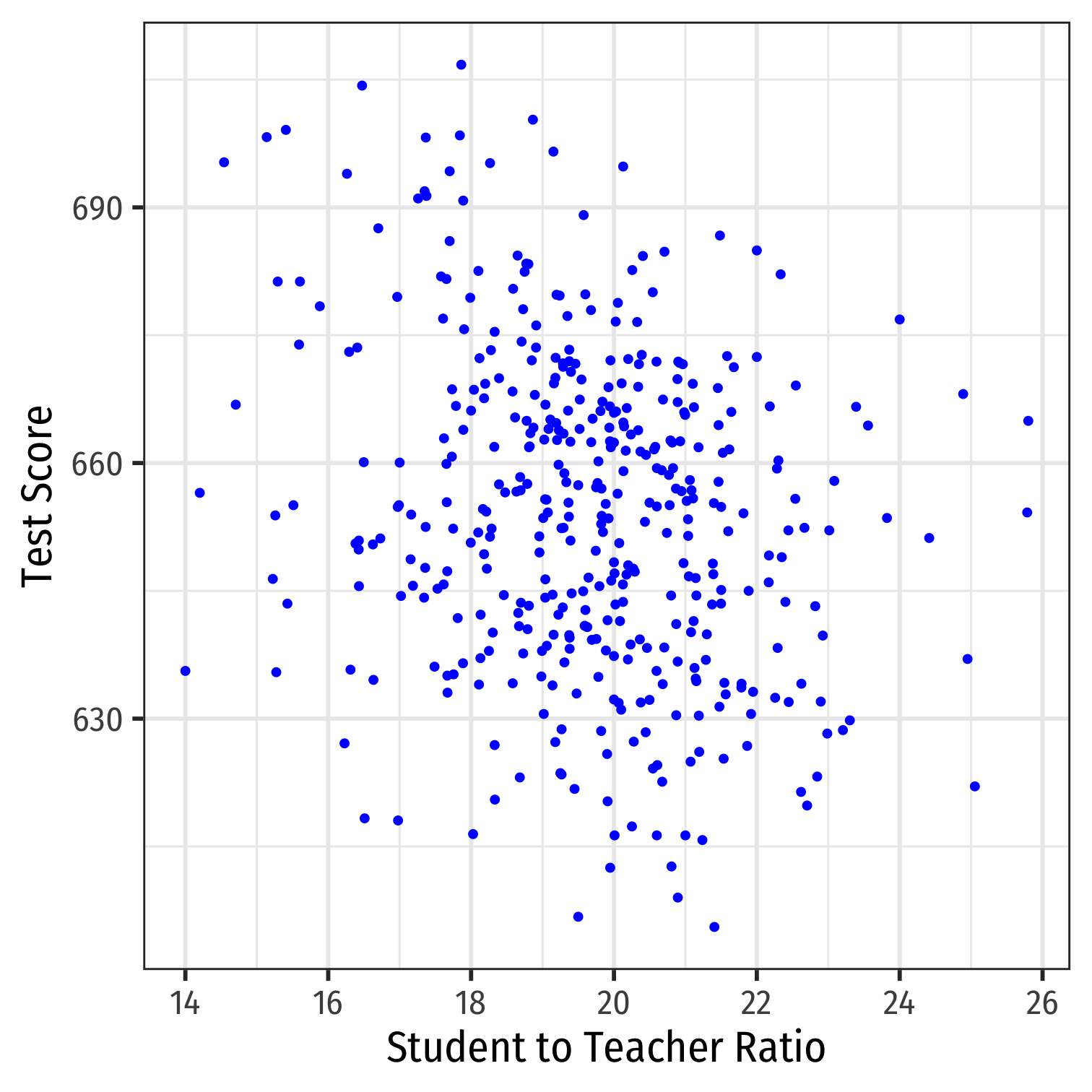
Class Size Example: Slope I
- If we change (Δ) the class size by an amount, what would we expect the change in test scores to be?
β=change in test scorechange in class size=Δtest scoreΔclass size
- If we knew β, we could say that changing class size by 1 student will change test scores by β

Class Size Example: Slope II
- Rearranging:
Δtest score=β×Δclass size

Class Size Example: Slope II
- Rearranging:
Δtest score=β×Δclass size
- Suppose β=−0.6. If we shrank class size by 2 students, our model predicts:
Δtest score=−2×βΔtest score=−2×−0.6Δtest score=1.2

Class Size Example: Slope and Average Effect
test score=β0+β1×class size
The line relating class size and test scores has the above equation
β0 is the vertical-intercept, test score where class size is 0
β1 is the slope of the regression line
This relationship only holds on average for all districts in the population, individual districts are also affected by other factors

Class Size Example: Marginal Effects
- To get an equation that holds for each district, we need to include other factors
test score=β0+β1class size+other factors
For now, we will ignore these until Unit 3
Thus, β0+β1class size gives the average effect of class sizes on scores
Later, we will want to estimate the marginal effect (causal effect) of each factor on an individual district's test score, holding all other factors constant

Econometric Models Overview
Y=β0+β1X1+β2X2+u
Econometric Models Overview
Y=β0+β1X1+β2X2+u
- Y is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
Econometric Models Overview
Y=β0+β1X1+β2X2+u
- Y is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- X1 and X2 are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
Econometric Models Overview
Y=β0+β1X1+β2X2+u
- Y is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- X1 and X2 are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
- Our data consists of a spreadsheet of observed values of (X1i,X2i,Yi)
Econometric Models Overview
Y=β0+β1X1+β2X2+u
- Y is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- X1 and X2 are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
Our data consists of a spreadsheet of observed values of (X1i,X2i,Yi)
To model, we "regress Y on X1 and X2"
Econometric Models Overview
Y=β0+β1X1+β2X2+u
- Y is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- X1 and X2 are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
Our data consists of a spreadsheet of observed values of (X1i,X2i,Yi)
To model, we "regress Y on X1 and X2"
β0 and β1 are parameters that describe the population relationships between the variables
- unknown! to be estimated!
Econometric Models Overview
Y=β0+β1X1+β2X2+u
- Y is the dependent variable of interest
- AKA "response variable," "regressand," "Left-hand side (LHS) variable"
- X1 and X2 are independent variables
- AKA "explanatory variables", "regressors," "Right-hand side (RHS) variables", "covariates"
Our data consists of a spreadsheet of observed values of (X1i,X2i,Yi)
To model, we "regress Y on X1 and X2"
β0 and β1 are parameters that describe the population relationships between the variables
- unknown! to be estimated!
- u is the random error term
- 'U'nobservable, we can't measure it, and must model with assumptions about it
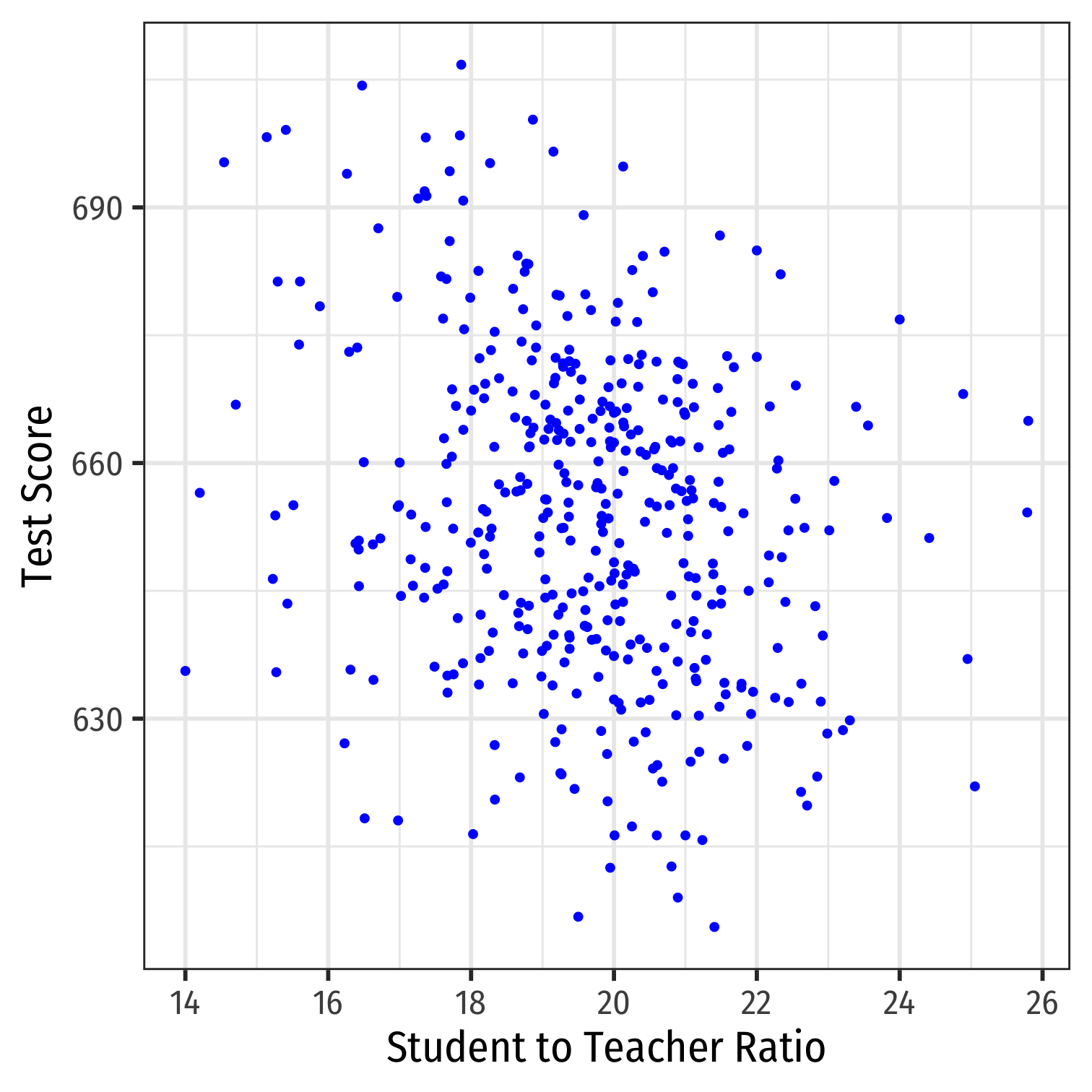
The Population Regression Model
How do we draw a line through the scatterplot? We do not know the "true" β0 or β1
We do have data from a sample of class sizes and test scores1
So the real question is, how can we estimate β0 and β1?
1 Data are student-teacher-ratio and average test scores on Stanford 9 Achievement Test for 5th grade students for 420 K-6 and K-8 school districts in California in 1999, (Stock and Watson, 2015: p. 141)
Deriving OLS
Deriving OLS
- Suppose we have some data points

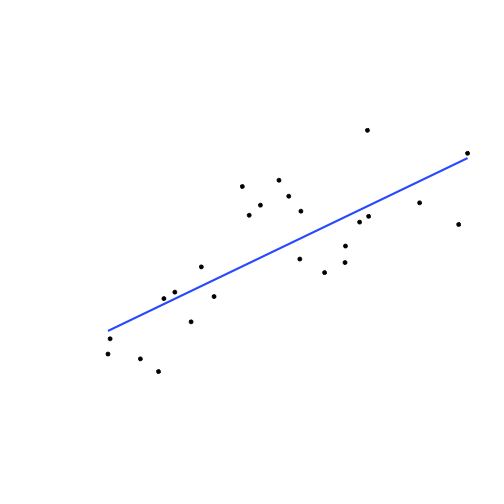
Deriving OLS
- Suppose we have some data points
- We add a line
Deriving OLS
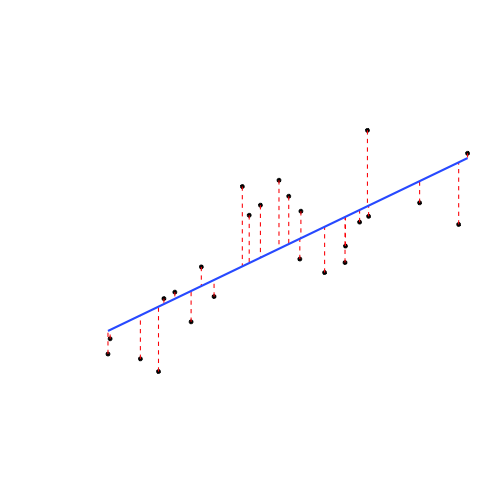
- Suppose we have some data points
- We add a line
- The residual, ˆu of each data point is the difference between the actual and the predicted value of Y given X:
ui=Yi−^Yi
Deriving OLS
- Suppose we have some data points
- We add a line
- The residual, ˆu of each data point is the difference between the actual and the predicted value of Y given X:
ui=Yi−^Yi
- We square each residual
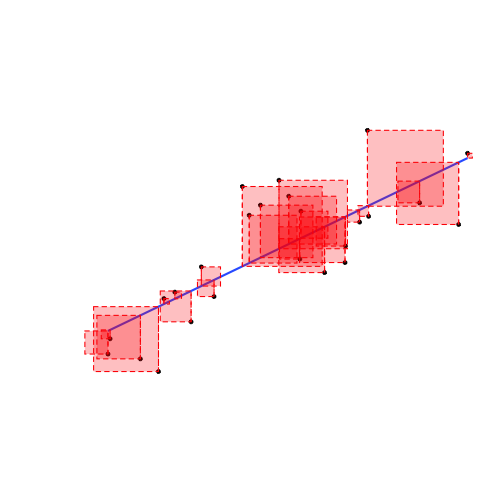
Deriving OLS
- Suppose we have some data points
- We add a line
- The residual, ˆu of each data point is the difference between the actual and the predicted value of Y given X:
ui=Yi−^Yi
- We square each residual
- Add all of these up: Sum of Squared Errors (SSE)
SSE=n∑i=1u2i
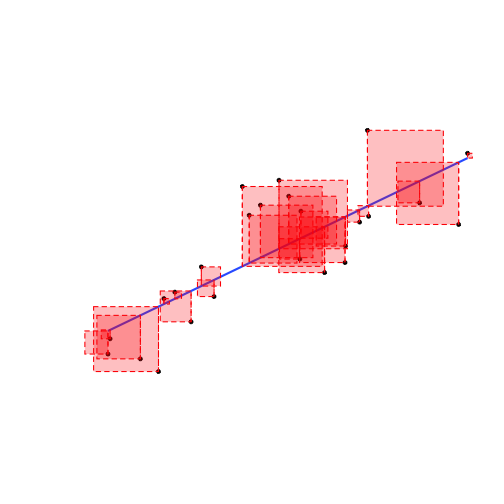
Deriving OLS
- Suppose we have some data points
- We add a line
- The residual, ˆu of each data point is the difference between the actual and the predicted value of Y given X:
ui=Yi−^Yi
- We square each residual
- Add all of these up: Sum of Squared Errors (SSE)
SSE=n∑i=1u2i
- The line of best fit minimizes SSE
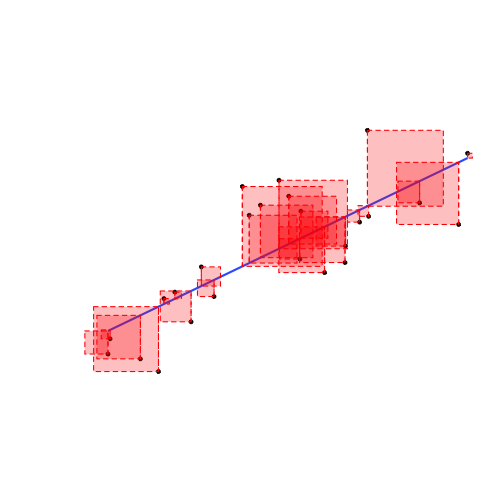
O rdinary L east S quares Estimators
- The Ordinary Least Squares (OLS) estimators of the unknown population parameters β0 and β1, solve the calculus problem:
minβ0,β1n∑i=1[Yi−(β0+β1Xi⏟^Yi)⏟u]2
O rdinary L east S quares Estimators
- The Ordinary Least Squares (OLS) estimators of the unknown population parameters β0 and β1, solve the calculus problem:
minβ0,β1n∑i=1[Yi−(β0+β1Xi⏟^Yi)⏟u]2
- Intuitively, OLS estimators minimize the average squared distance between the actual values (Yi) and the predicted values (ˆYi) along the estimated regression line
The OLS Regression Line
- The OLS regression line or sample regression line is the linear function constructed using the OLS estimators:
^Yi=^β0+^β1Xi
The OLS Regression Line
- The OLS regression line or sample regression line is the linear function constructed using the OLS estimators:
^Yi=^β0+^β1Xi
- ^β0 and ^β1 ("beta 0 hat" & "beta 1 hat") are the OLS estimators of population parameters β0 and β1 using sample data
The OLS Regression Line
- The OLS regression line or sample regression line is the linear function constructed using the OLS estimators:
^Yi=^β0+^β1Xi
^β0 and ^β1 ("beta 0 hat" & "beta 1 hat") are the OLS estimators of population parameters β0 and β1 using sample data
The predicted value of Y given X, based on the regression, is E(Yi|Xi)=^Yi
The OLS Regression Line
- The OLS regression line or sample regression line is the linear function constructed using the OLS estimators:
^Yi=^β0+^β1Xi
^β0 and ^β1 ("beta 0 hat" & "beta 1 hat") are the OLS estimators of population parameters β0 and β1 using sample data
The predicted value of Y given X, based on the regression, is E(Yi|Xi)=^Yi
The residual or prediction error for the ith observation is the difference between observed Yi and its predicted value, ^ui=Yi−^Yi
The OLS Regression Estimators
- The solution to the SSE minimization problem yields:1
The OLS Regression Estimators
- The solution to the SSE minimization problem yields:1
ˆβ0=ˉY−^β1ˉX
The OLS Regression Estimators
- The solution to the SSE minimization problem yields:1
ˆβ0=ˉY−^β1ˉX
ˆβ1=n∑i=1(Xi−ˉX)(Yi−ˉY)n∑i=1(Xi−ˉX)2=sXYs2X=cov(X,Y)var(X)
1 See tomorrow's class notes page for proofs.
Our Class Size Example in R
Class Size Scatterplot (Again)
scatterThere is some true (unknown) population relationship: test score=β0+β1×str
β1=Δtest scoreΔstr=??
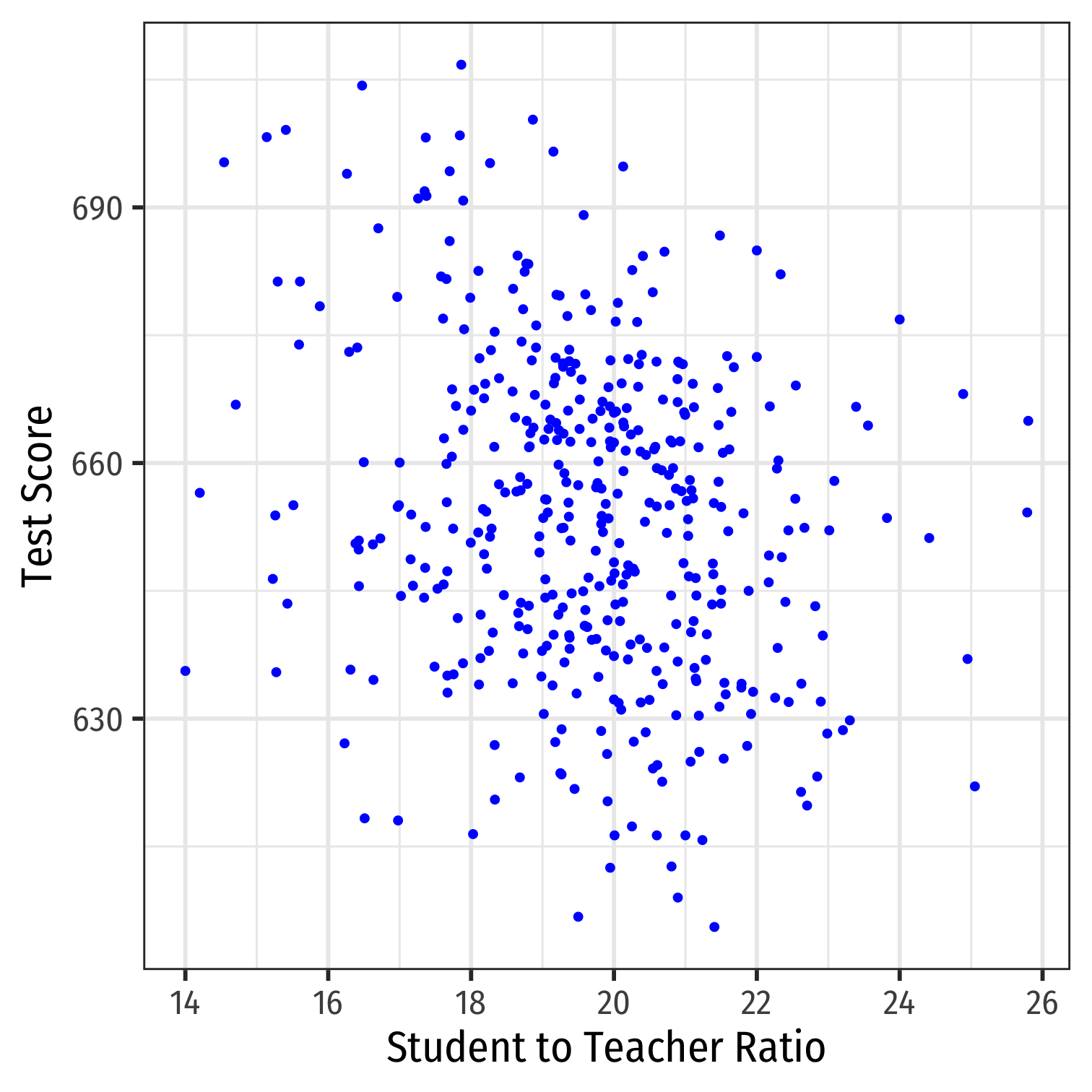
Class SIze Scatterplot with Regression Line
scatter+ geom_smooth(method = "lm", color = "red")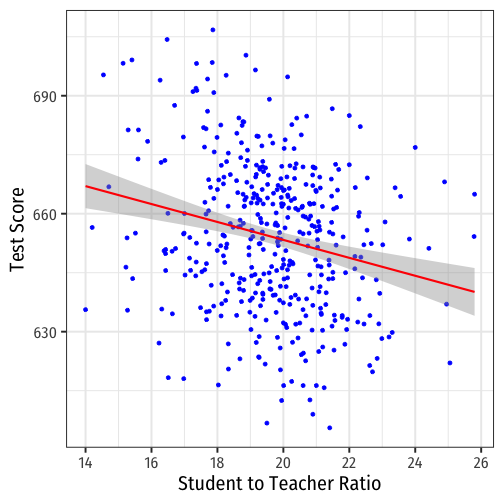
OLS in R
# run regression of testscr on strschool_reg <- lm(testscr ~ str, data = CASchool)- Format for regression is
lm(y ~ x, data = df) yis dependent variable (listed first!)~means "modeled by"xis the independent variabledfis the dataframe where the data is stored
OLS in R II
# look at reg objectschool_reg## ## Call:## lm(formula = testscr ~ str, data = CASchool)## ## Coefficients:## (Intercept) str ## 698.93 -2.28- Stored as an
lmobject calledschool_reg, alistobject
OLS in R III
summary(school_reg) # get full summary## ## Call:## lm(formula = testscr ~ str, data = CASchool)## ## Residuals:## Min 1Q Median 3Q Max ## -47.727 -14.251 0.483 12.822 48.540 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 698.9330 9.4675 73.825 < 2e-16 ***## str -2.2798 0.4798 -4.751 2.78e-06 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 18.58 on 418 degrees of freedom## Multiple R-squared: 0.05124, Adjusted R-squared: 0.04897 ## F-statistic: 22.58 on 1 and 418 DF, p-value: 2.783e-06Looking at the
summary, there's a lot of information here!These objects are cumbersome, come from a much older, pre-
tidyverseepoch ofbase RLuckily, we now have
tidyways of working with regressions!
Tidy OLS in R: broom I

The
broompackage allows us to tidy up regression objects1The
tidy()function creates a tidytibbleof regression output
# load packageslibrary(broom)# tidy regression outputtidy(school_reg)## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 699. 9.47 73.8 6.57e-242## 2 str -2.28 0.480 -4.75 2.78e- 61 See more at broom.tidyverse.org.
Tidy OLS in R: broom II

The
broompackage allows us to tidy up regression objects1The
tidy()function creates a tidytibbleof regression output
# load packageslibrary(broom)# tidy regression output (with confidence intervals!)tidy(school_reg, conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 699. 9.47 73.8 6.57e-242 680. 718. ## 2 str -2.28 0.480 -4.75 2.78e- 6 -3.22 -1.341 See more at broom.tidyverse.org.
More broom Tools: glance
glance()shows us a lot of overall regression statistics and diagnostics- We'll interpret these in the next lecture and beyond
# look at regression statistics and diagnosticsglance(school_reg)## # A tibble: 1 x 11## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl>## 1 0.0512 0.0490 18.6 22.6 2.78e-6 2 -1822. 3650. 3663.## # … with 2 more variables: deviance <dbl>, df.residual <int>More broom Tools: augment
# add regression-based values to dataaugment(school_reg)## # A tibble: 420 x 9## testscr str .fitted .se.fit .resid .hat .sigma .cooksd .std.resid## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 691. 17.9 658. 1.24 32.7 0.00442 18.5 0.00689 1.76 ## 2 661. 21.5 650. 1.28 11.3 0.00475 18.6 0.000893 0.612## 3 644. 18.7 656. 1.01 -12.7 0.00297 18.6 0.000700 -0.685## 4 648. 17.4 659. 1.42 -11.7 0.00586 18.6 0.00117 -0.629## 5 641. 18.7 656. 1.02 -15.5 0.00301 18.6 0.00105 -0.836## 6 606. 21.4 650. 1.24 -44.6 0.00446 18.5 0.0130 -2.40 ## 7 607. 19.5 654. 0.909 -47.7 0.00239 18.5 0.00794 -2.57 ## 8 609 20.9 651. 1.09 -42.3 0.00343 18.5 0.00895 -2.28 ## 9 612. 19.9 653. 0.919 -41.0 0.00244 18.5 0.00597 -2.21 ## 10 613. 20.8 652. 1.07 -38.9 0.00329 18.5 0.00723 -2.09 ## # … with 410 more rowsaugment()creates useful new variables in the storedlmobject.fittedare fitted (predicted) values from model, i.e. ˆYi.residare residuals (errors) from model, i.e. ˆui
Class Size Regression Result I
- Using OLS, we find:
^test score=689.9−2.28×str
Class Size Regression Result II
- There's a great package called
equatiomaticthat prints this equation inmarkdownor LATEX.
testscr=698.93−2.28(str)+ϵ
Class Size Regression Result II
- There's a great package called
equatiomaticthat prints this equation inmarkdownor LATEX.
testscr=698.93−2.28(str)+ϵ
Here was my code:
# install.packages("equatiomatic") # install for first uselibrary(equatiomatic) # load itextract_eq(school_reg, # regression lm object use_coefs = TRUE, # use names of variables coef_digits = 2, # round to 2 digits fix_signs = TRUE) # fix negatives (instead of + -)## $$## \text{testscr} = 698.93 - 2.28(\text{str}) + \epsilon## $$- In
Rchunk inR markdown, set{r, results="asis"}to print this raw output to be rendered
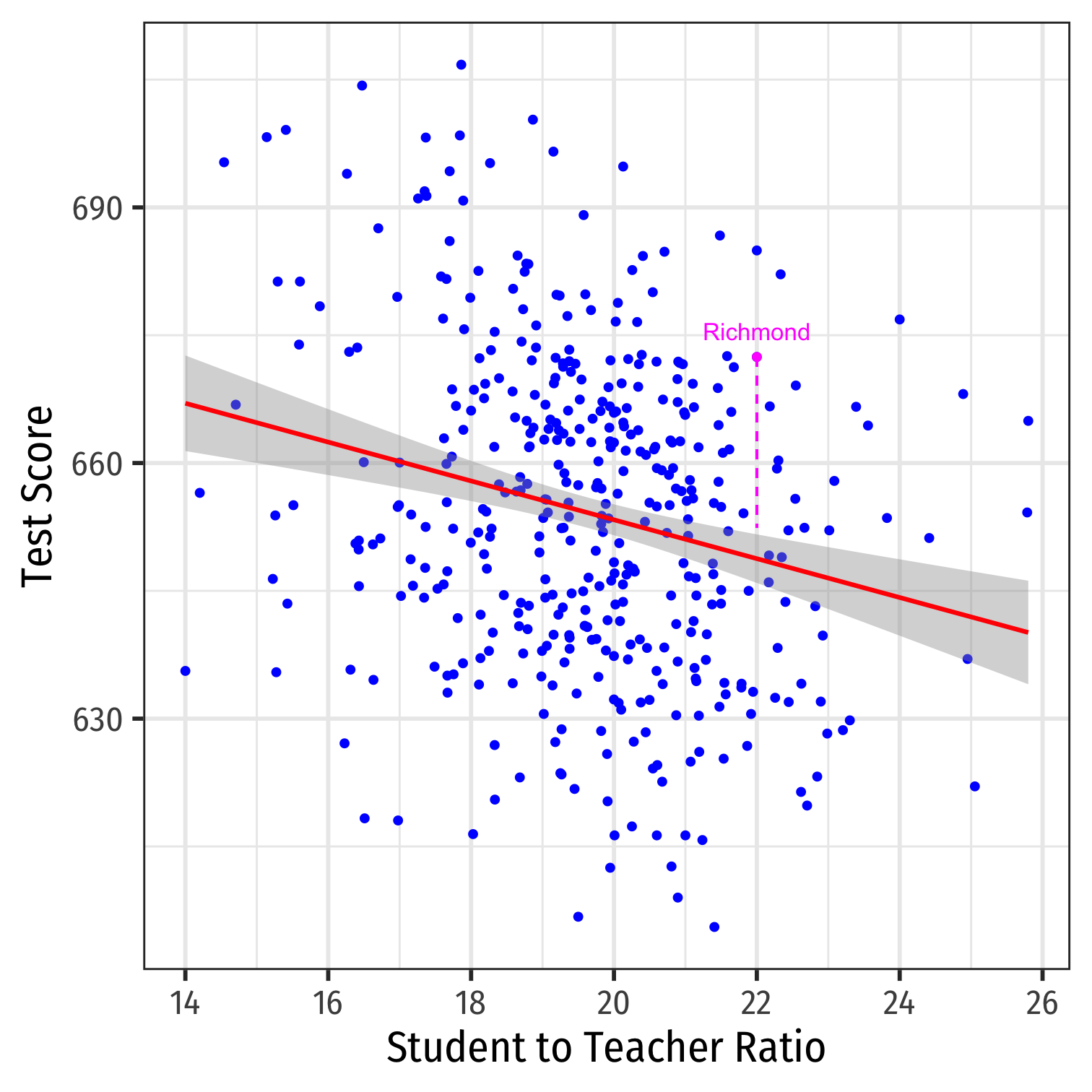
Class Size Regression: A Data Point
- One district in our sample is Richmond, CA:
CASchool %>% filter(district=="Richmond Elementary") %>% dplyr::select(district, testscr, str)## # A tibble: 1 x 3## district testscr str## <chr> <dbl> <dbl>## 1 Richmond Elementary 672. 22Predicted value: ^Test ScoreRichmond=698−2.28(22)≈648
Residual: ˆuRichmond=672−648≈24